Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	Математике

дисциплине

Выполнил(а) студент(ка)	Шестеренко Никита Романович
			фамилия имя отчество
Идентификационный номер:		2201-160

Пермь 2022
Задание 1. Решить систему линейных алгебраических уравнений:



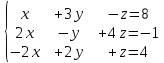
Коэффициенты левых частей уравнений системы образуют матрицу:


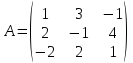
Система линейных уравнений имеет единственное решение тогда и только тогда, когда определитель матрицы системы отличен от нуля.



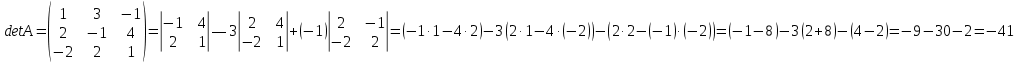
В этом случае решение находят по формулам Крамера:



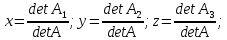
где матрицы A₁;A₂; A₃ получаются из матрицы системы A заменой соответственно первого, второго и третьего столбца столбцом свободных членов.

---

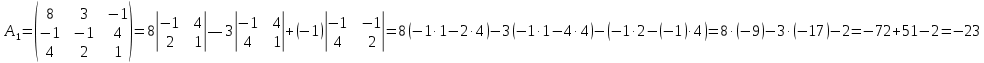
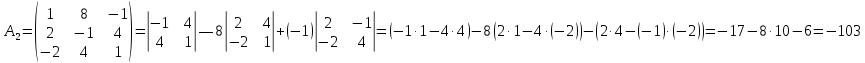
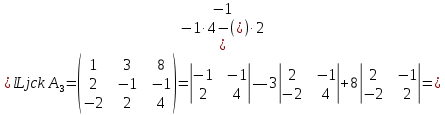
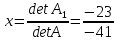
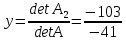
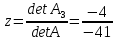
Проверка:



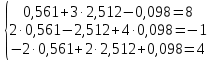
Ответ:

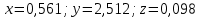
Задание 2.

Дано: z₁=1-5i z₂=-3+2i

Выполнить действия:

1. 
   а) z₁ + z₂
   

Решение:



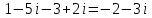
б) z₁ ∙ z₂

Решение:



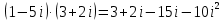
Учитывая, что 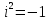, получим: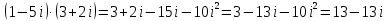



б) z₁/z₂

Решение:



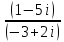
Учитывая, что 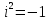, умножая числитель и знаменатель на сопряженную дробь (1-i), получим: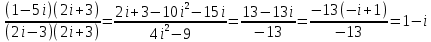



Задание 3 Найти математическое ожидание и дисперсию, заданной законом распределения

Дано:

X	2	3	4	5
p	0,4	0,3	0,1	0,2

Решение:

1. 
   Математическое ожидание дискретной случайной величины вычисляем по формуле:
   

---

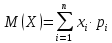
Подставляем данные задачи в эту формулу, получим:

2. 
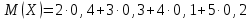
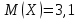
   Дисперсию дискретной случайной величины вычисляем по формуле:
   

3. 
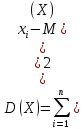
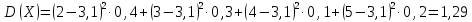
   Среднее квадратичное отклонение:
   

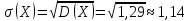
Задание 4. Вычислить предел:



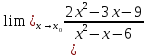
при x₀ 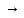2

Решение:


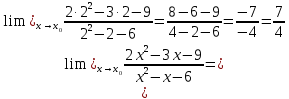
Ответ:

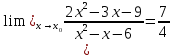
Задание 5. Найти производную функции


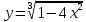
Применяя формулы производных:

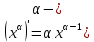постоянная)

Согласно теореме:

если функци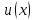и и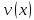 дифференцируемы на некотором интервале, то на этом интервале:

,

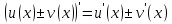т.е. производная суммы (разности) функций равна сумме (разности) любого конечного числа функций.



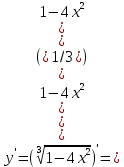
Ответ:
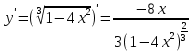
Задание 6. Вычислить неопределенный интеграл:



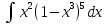
Решение:

Вводим новую переменную: t= 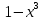=> dt=-3x²dx =>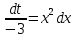

Получим:



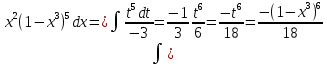
Ответ:

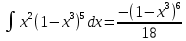
Список использованной литературы:

---

1. 
   Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 2017. – 224 с.
   
2. 
   Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. 1. – М.: Высшая школа, 2017. – 304 с.
   

---

Смотрите также файлы

• Лабораторная работа 5 Метод наименьших квадратов студент гр. Ибс21 Проверил доцент кафедры пмиСА.docx

• ыса мерзімді саба жоспары Тексерілді.docx

• Основы моральнополитической готовности сотрудников к выполнению поставленных задач по предназначению.doc

• Жусан иісі (Сайын Мратбеков).docx

• Методические указания по выполнению практических и самостоятельных работ для бакалавров направления.docx