МИНПРОСВЕЩЕНИЯ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Волгоградский государственный социально-педагогический университет»
Факультет дошкольного и начального образования

Кафедра педагогики дошкольного образования

Контрольная работа

«Использование моделей в процессе обучения детей дошкольного возраста решению арифметических задач по методике Н.Ю. Непомнящей»

по дисциплине: «методика математического развития»

по направлению 44.03.01 «Педагогическое образование»

профиль подготовки бакалавров «Дошкольное образование»

Подготовила: студентка _____ курса

Группа __________

Мартычева Елена Николаевна

Проверила:

Забровская Ольга Васильевна,

канд. пед. наук, доцент

Волгоград

2022
1.Виды арифметических задач, применяемых в стенах дошкольных образовательных организаций

В детском саду дети решают самые простые задачи. Содержание задач и их количественные данные направлены на то, чтобы познакомить детей с окружающей жизнью. О необходимости этого говорил ещё К.Д. Ушинский: «Задачи выбираются самые практические из жизни, с которой дети знакомы, и у хороших преподавателей дело выходит так, что арифметическая задача есть весьма занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая и статистическая тема и упражнения в языке».

Простые задачи, т.е. задачи, решаемые одним действием (сложением или вычитанием), принято делить на следующие группы:

К первой группе относятся те задачи, при которых дети усваивают конкретный смысл каждого из арифметических действий. Это задачи на нахождение суммы двух чисел и на нахождение остатка.

Ко второй группе относятся простые задачи, при решении которых надо осмыслить связь между компонентами и результатами арифметических действий. Это задачи на нахождение неизвестных компонентов:

а) нахождение слагаемого по известной сумме и второму слагаемому;

б) нахождение второго слагаемого по известной сумме и первому слагаемому;

в) нахождение уменьшаемого по известным вычитаемому и разности;

г) нахождение вычитаемого по известным уменьшаемому и разности.

К третьей группе относятся простые задачи, связанные с понятием разностных отношений:

а) увеличение числа на несколько единиц;

---

б) уменьшение числа на несколько единиц.

Также есть и другие разновидности задач, в которых раскрывается новый смысл арифметических действий. В зависимости от используемого для составления задач наглядного материала они подразделяются на:

- задачи - картинки

- задачи - иллюстрации

- задачи - драматизации.

Обучение дошкольников решению арифметических задач проходит через ряд взаимосвязанных между собой этапов.

1. Подготовительный этап - основная цель этого этапа - организовать систему упражнений по выполнению операций над множествами. Так, подготовкой к решению задач на сложение являются упражнения на объединение множеств. Упражнения на выделение части множества проводятся для подготовки детей решению задач на вычитание. С помощью операций над множествами раскрывается отношение «целое-часть», доводиться до понимания смысл выражений «больше на…», «меньше на…».

2. Работа над структурой задачи. На этом этапе учат составлять задачи, устанавливать связи между данными и искомым и на этой основе выбирать для решения необходимое практическое действие. Для понимания структуры задачи лучше всего использовать задачи-драматизации. Педагог знакомит детей со словом задача и при разборе составленной задачи подчёркивает необходимость числовых данных и вопросов: «Что известно?», «Что нужно знать?».

3. Обучение формулированию арифметического действия сложения и вычитания - задача третьего этапа. Когда дети научились находить ответ на вопрос задачи, опираясь на свои знания последовательности чисел, связей и отношений между ними. Теперь же нужно познакомить с арифметическими действиями сложения и вычитания, раскрыть их смысл, научить формулировать их и «записывать» с помощью цифр и знаков в виде числового примера.
2. Методика решению арифметических задач Н.И. Непомнящей

В методике Н.И. Непомнящей используется выделение в задаче частей и целого и в зависимости от того, что неизвестно (часть или целое) выбирается действие, которым и решается задача.  В данной методике обучение детей старшего дошкольного возраста решению простых текстовых задач осуществляется в два этапа.

---

На первом - детей учат объединить, разъединить и уравнивать совокупности предметов, устанавливать связи и отношения между целым и частями, фиксировать их. На втором - у дошкольников вырабатывают умение анализировать и решать простые арифметические задачи.

Рассмотрим работу на первом этапе. Первоначально дошкольников учат видеть предметы в целом, определять, по какому признаку они объединены в целое. Детей упражняют в выделении предметов по виду, цвету, форме, размеру, учат практически определять, в какой из двух сравниваемых групп предметов больше (меньше) или их количество равно, раскрывают смысл отношений больше, меньше, равно.

Для занятий следует использовать игрушки разных видов в равном и неравном количестве; предметные картинки, геометрические фигуры разного цвета, формы, размеров; шнурки, ленточки разного цвета и длины. Например, воспитатель ставит на стол 5 матрешек и 5 пирамидок. Обводит круговым движением все игрушки и спрашивает: «Как одним словом назвать все это? Каким словом, не считая, можно сказать, сколько игрушек на столе? Из каких видов игрушек составлена эта группа?» (Круговым движением обводит целое и его части.) После того как дети определят, что на столе стоят игрушки (группа), одна часть которых - матрешки, а другая - пирамидки, и круговым движением выделят совокупность и составляющие ее части, ставится следующий вопрос, подводящий детей к новому способу выделения целого и частей в нем: «Можно ли сделать так, чтобы было видно, что в целой группе игрушек две группы?» (Медленным круговым движением воспитатель выделяет целое и части.) Для этой цели можно использовать цветные шнурки и ленточки. После трех-четырех подобных упражнений уже на другом материале дети усваивают, что в целом (окаймленном длинным шнурком) имеются две части (окаймленные шнурками другого цвета).

В целях закрепления полученных знаний можно задать вопрос: «Как определить, не считая, чего больше, меньше или поровну матрешек или пирамидок?». Отношения больше, меньше рассматриваются в связи друг с другом (например, если квадратов больше, чем треугольников, то треугольников меньше, чем квадратов).

В дальнейшем дети продолжают тренироваться в выделении общих характерных свойств целой совокупности, составляющих ее частей и отдельных предметов, дошкольников учат графически изображать структуру целого с помощью окружностей, устанавливать соответствие между объектами частей

---

, соединяя их линиями.

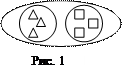 Для ознакомления детей с данным материалом используется следующее упражнение: воспитатель на доске изображает несколько красных треугольников и несколько синих квадратов. В процессе работы с детьми определяется, что все геометрические фигуры являются целым, их можно поместить в большой круг (обводят мелом), целое состоит из частей – треугольников и квадратов, эти части также можно выделить, но кругами поменьше (обводят мелом) - рис. 1.

Затем детям предлагается подумать, как можно, не считая, определить, чего больше (меньше, поровну) - квадратов или треугольников. После этого им показывают новый способ, установления соответствия между объектами двух сравниваемых частей с помощью линий.

Для того, чтобы ознакомить детей с другими видами моделей полезно предложить им выполнить следующее задание: на доске вывешивают картину-панно с видом озера и плавающими по нему утками и гусями и предлагают рассказать, какое целое и какие части изображены на картине и как бы следовало это зарисовать у себя в тетради. Но так как рисовать уток и гусей сложно и долго, ребятам предлагается подумать, как можно быстрее зарисовать объекты целого. Дети высказывают свои предложения зарисовать их крестиками, палочками, точками, геометрическими фигурами и т.п. Выслушав суждения детей, педагог говорит, что сами предметы совокупности можно и не обозначать, а нарисовать только большой круг, обозначающий целое, в нем - маленькие круги, обозначающие части, а предметы обозначить точками. Далее дети сами составляют целое и части из геометрических фигур, рассказывая о том, что делали и как изображали их в своих тетрадях.

Выполняя подобные упражнения, дети знакомятся с простейшими понятиями целое, часть, предмет, объект целого, осознают принадлежность предмета, а также части целому.

Графическая зарисовка создает для детей наглядную модель отношений между целым и частями, помогает усвоить характерные их свойства. Дети начинают понимать, что каждый предмет, принадлежащий части, принадлежит одновременно и целому. Однако часть может и не утрачивать своего индивидуального характерного свойства: например, часть - квадратыили часть - треугольники, сохраняя свои индивидуальные свойства, одновременно приобретает и общее характерное свойство целого - фигуры.

Дошкольники учатся устанавливать отношение 

---

целое - часть, выполнять уравнивание, определять связи данного отношения, узнавать и фиксировать это в виде диаграмм.

Усвоение детьми структуры целого позволяет подвести их к пониманию объединения совокупностей. С этой целью можно провести следующее упражнение: из карточек с изображением полевых цветов детям предлагается составить букет и рассказать, как они его составили, какое получилось целое и из каких частей оно составлено. После этого данная ситуация изображается на доске в той последовательности, в какой составляли букет: ребята изображают точками ромашки и обводят получившуюся совокупность небольшой окружностью, затем изображают крестиками васильки и также обводят совокупность окружностью, чтобы показать, что обе совокупности объединены, рисуют общую окружность, включая в нее две небольшие.

При объяснении внимание дошкольником обращается на то, что имели место две разные совокупности, каждая из которых состояла из однородных предметов, но когда обе совокупности соединили, то получилось целое, состоящее из разнородных предметом, имеющих один общий признак - букет цветов, и дети это должны объяснить так: «Я взял васильки и ромашки, соединил их вместе и получился букет цветов. Букет цветов - это целое, в нем две части: одна часть - васильки, а другим - ромашки».

Аналогичные упражнения выполняются с изображени­ями животных, транспорта, посуды, мебели и др. После того как дети поупражняются в выполнении операции объединения совокупностей предметов и научатся выделять отношения между целым и частями, внимание детей обращается на количественные отношения между целым и частями: «Чего больше - всех цветов или только ромашек (васильков)? Почему?»

В результате упражнений детей подводят к обобщению: «В букете цветов столько, сколько ромашек и ва­сильков вместе. В стаде животных столько, сколько коз и коров вместе». Воспитатель предлагает детям самим назвать целое, состоящее из двух частей (мебель, посуда, транспорт и т.д.).

Обучая дошкольников устанавливать отношения больше-меньшемежду целым и частями, между отдельными частями предметов, рекомендуется учить их записывать эти отношения знаками >, <, =. Например, дети составляют букет из кленовых и дубовых листьев. Возникает вопрос: «Какая из частей больше (меньше)?». Дошкольникам предлагают те и другие листья разложить рядами друг под другом или изобразить их точками и крестиками, расположив точки и крестики рядами так, чтобы стало видно, каких листьев больше, а каких меньше. Воспитатель спрашивает: «Как записать это знаками?». Дети не знают. Воспитатель изображает на доске знаки >, 

---

Смотрите также файлы

• .docx

• Приемы развития функциональной грамотности на уроках математики в начальной школе.docx

• Группа 4410 Аканова Айгерим. Задача 6.docx

• Жарптица миф или реальность Устинов Никита.docx

• Ф гос 1 пик.docx