Министерство науки и высшего образования российской федерацииФедеральное государственное автономное образовательное учреждениевысшего образования«Южно-Уральский государственный университет(национальный исследовательский университет)»Кафедра «Инфокоммуникационные технологии»«Ответы на вопросы»ОТЧЕТ ПО ПРАКТИЧЕСКОму Заданию № 1по дисциплине «Радиотехнические цепи и сигналы»Проверил: Рагозин А.Н. «___» __________________ 2022 г.Выполнили: Студент группы КЭ-310 _________________ Нагаев Д.В. 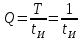«_03_»________12________ 2022 г.Челябинск 2022Вопрос 1.Как ширина спектра периодической последовательности импульсных сигналов зависит от длительности одиночного импульса?Ответ: Чем меньше длительность импульса, тем шире спектр и наоборот.Вопрос 2.Как параметры спектра периодической последовательности импульсов зависят от формы одиночного импульса?Ответ:Спектр периодической последовательности импульсов будет зависеть от длительности импульса, и как следствие скважности, т.к. она влияет на ширину спектра и его амплитуду.Вопрос 3.Какие параметры спектра периодической последовательности импульсов зависят от периода повторения импульсов?Ответ:При увеличении периода повторения импульсов и при постоянной длительности импульса, ширина "лепестка" остается неизменной и уменьшается амплитуда гармоник и расстояние между ними, а также изменяется положение гармоник на оси частот.Вопрос 4.Как отличаются спектры периодической последовательности импульсов симметричной формы (например, колоколообразной) от спектров периодической последовательности импульсов несимметричной формы (например, синусоидальной или односторонней пилообразной)?

---

Ответ:Амплитудные спектры периодической последовательности импульсов симметричной формы не отличаются от спектров периодической последовательности импульсов несимметричной формы. Отличаются фазовые спектры. Гармоники несимметричного импульса имеют разные фазовые сдвиги.Вопрос 5.Что такое техническая ширина спектра сигнала и чем она отличается от абсолютной ширины спектра?Ответ:Под технической шириной спектра сигнала подразумевается полоса частот, в которой сосредоточена основная часть энергии сигнала. 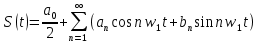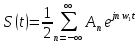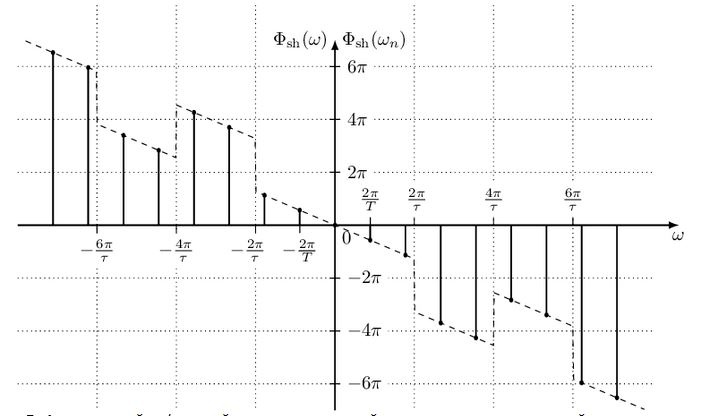Абсолютная ширина спектра бесконечна, а техническую ограничивают на определенном уровне.Вопрос 6.Запишите математическое определение спектрального ряда для периодического сигнала в комплексной и тригонометрической форме.Ответ:Тригонометрическая форма периодического сигнала:Комплексная форма периодического сигнала:Вопрос 7.Как временной сдвиг периодической последовательности импульсов влияет на характеристики её спектра.Ответ:Сдвиг периодического сигнала во времени не изменяет амплитудный спектр сигнала, но добавляет линейную составляющую к фазовому спектру сигнала.Вопрос 8.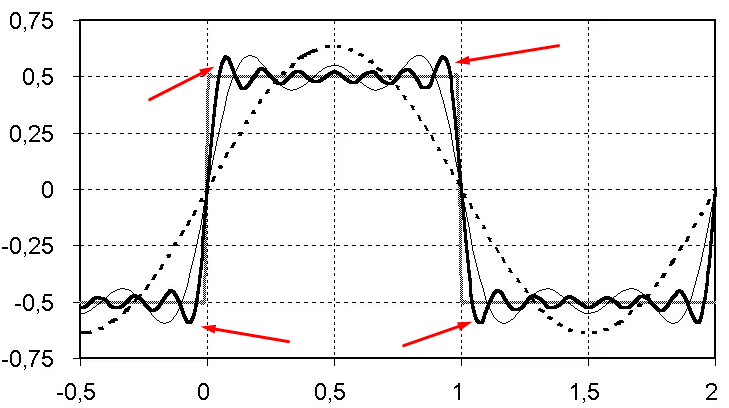Дайте определение краевого эффекта (явление Гиббса). Как этот эффект проявляется при аппроксимации импульсного сигнала усечённым рядом?Ответ:Эффект Гиббса проявляется в скачках амплитуды на точках разрыва функции. 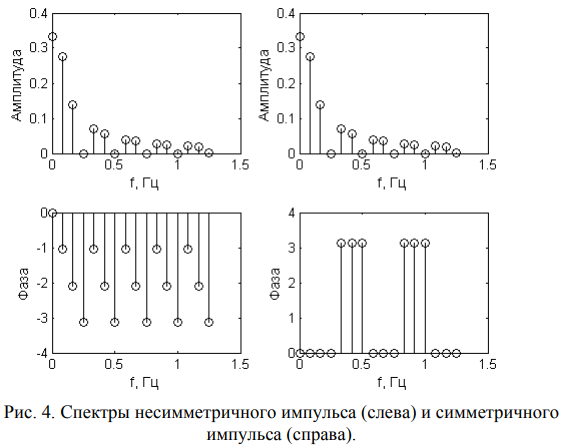При аппроксимации импульсного сигнала усеченным рядом по краям появляются превышения.Вопрос 9.Как отличаются спектры периодической последовательности импульсов симметричной формы (например, колоколообразной) от спектров периодической последовательности импульсов несимметричной формы (например, синусоидальной или односторонней пилообразной)?Ответ:Сравним спектры несимметричного и симметричного прямоугольного импульса длительностью τ и периодом повторения T . По формуле вычисляем коэффициенты, полагаем, что амплитуда импульса равна

---

1. 
   Для несимметричного импульса:
   

2. 
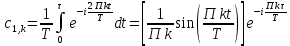
   Для симметричного импульса:
   

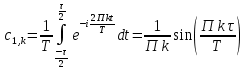
(Амплитудные спектры совпадают, а поведение фазовых спектров отличается. По амплитудным спектрам видно, что амплитуда каждой третьей гармоники равна нулю)Вопрос 10.Можно ли аппроксимировать одиночный импульс рядом по системе гармонических функций с заданной точностью?Ответ:Фурье показал, что любую сложную функцию можно представить (аппроксимировать) в виде конечной или бесконечной суммы ряда кратных гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Этой функцией может быть, в частности, ток или напряжение в цепи. Солнечный луч, разложенный призмой на спектр цветов, представляет собой физический аналог математических преобразований Фурье.Вопрос 11. 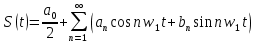Запишите математическое определение спектрального ряда для периодического сигнала в комплексной и тригонометрической форме.Ответ:Из математического анализа известно, что периодический сигнал можно представить в виде тригонометрического ряда Фурье: Формула Эйлера связывает действительные тригонометрические функции и комплексную экспоненту:Вопрос 12.Каким образом необходимо изменить гармонический ряд, чтобы изменить временное положение синтезируемого сигнала?Ответ:Смещение сигнала по оси ординат изменяет амплитудный спектр (составляющую, соответствующую нулевой частоте), а сдвиг сигнала во времени - изменяет фазовый спектр сигнала. Таким образом, чтобы изменить временное положение синтезируемого сигнала, необходимо поменять фазы гармоник в гармоническом ряду.

---

Вопрос 13.Очевидно, что наиболее рациональным для практического использования является представление сигнала спектральным рядом с более быстрым убыванием амплитуды гармонических компонентов. Какой параметр периодической последовательности и как влияет на сходимость спектрального ряда.Ответ:Основным параметром, влияющим на сходимость спектрального ряда, является количество гармоник данного ряда (чем их больше – тем больше сходимость).Вопрос 14. Дайте определение теоремы Котельникова.Ответ:Теорема Котельникова устанавливает оптимальную величину интервалов дискретных сигналов. Согласно теореме - произвольный сигнал s(t), спектр которого ограничен некоторой частотой F_M (максимальная частота спектра сигнала) может быть полностью восстановлен по последовательности своих отчётных значений, следующих с интервалом времени: (t)=1/2*F_M.Вопрос 15.Приведите математическое описание процедуры дискретизации и структурную схему её осуществления.Ответ:Для того, чтобы получить дискретизированный сигнал, достаточно умножить функцию дискретизации на исходный непрерывный сигнал x(t).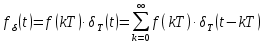Структурную схему можно представить в виде ключа, замыкающего цепь, по которой идет исходный сигнал, на очень короткие промежутки времени с интервалом T.Вопрос 16.Как определить практически приемлемый период дискретизации для реального импульсного сигнала конечной длительности?Ответ:Если отсчеты сигнала брать слишком редко, то быстрые изменения, скачки сигнала могут остаться незамеченными. Если же брать отсчеты слишком часто, то это будет неэффективно. Задача о выборе интервала дискретизации наиболее просто решается на основании теоремы Котельникова.Вопрос 17.Охарактеризуйте требования к характеристике реального сглаживающего фильтра для восстановления дискретизированного процесса.Ответ:Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление сигналов и фазо-частотная характеристика линейна (нет искажения формы сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.

---

Вопрос 18.


Почему для большинства реальных сигналов необходим в три пять раз меньший период дискретизации, чем по теореме Котельникова?

Ответ:

В соответствии с теоремой Котельникова отсчёты, следующие через интервалы времени ∆t=1/2*Fm могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза Fср = Fm. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Поэтому на практике выбирают ∆t несколько меньше (а иногда и в несколько раз меньше), чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала.

Вопрос 19.

Приведите структурную схему восстановления сигнала.

Ответ:



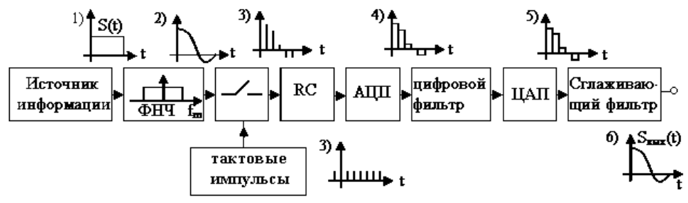
Рисунок – 1

На рисунке 1 приведена структурная схема канала передачи цифровой информации

1) Источник информации формирует сигнал, передающий информацию.

2) ФНЧ служит для ограничения спектра дискретизуемого сигнала.

3) Дискретизатор (электронный ключ) преобразовывает аналоговый сигнал в дискретный.

3) RC цепочка увеличивает длительность импульсов, то есть запоминает значение дискретного импульса на длительное время. Этот блок не обязателен.

4) АЦП (аналого-цифровой преобразователь) – служит для преобразования сигнала в цифровой двоичный код.

5) ЦАП (цифро-аналоговый преобразователь) – служит для преобразования цифрового сигнала в аналоговый.

6) Сглаживающий фильтр подавляет ВЧ составляющие. Это ФНЧ. После него на выходе канала из квантованного сигнала (5) получается аналоговый сигнал.

---

Смотрите также файлы

• Это одна из первых цивилизаций мира, принесшая мировой культуре крупнейшее колво различных духовных ценностей.docx

• Доклад по учебной дисциплине История социальной работы.rtf

• Самоанализ работы по организации проблемного обучения выступление на педагогическом совете Совершенствование методов обучения и воспитания в условиях сельской малокомплектной школы.docx

• Лабораторная работа Устранение неполадок, связанных с основным шлюзом.pdf

• Относительное равновесие жидкости во вращающемся сосуде.docx