Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
6. На месте пре­ступ­ле­ния были об­на­ру­же­ны четыре об­рыв­ка бумаги. След­ствие установило, что на них за­пи­са­ны фрагменты од­но­го IP-адреса. Кри­ми­на­ли­сты обозначили эти фраг­мен­ты буквами А, Б, В и Г:

 

4.243	116.2	13	.23
А	Б	В	Г

 

Восстановите IP-адрес. В от­ве­те укажите по­сле­до­ва­тель­ность букв, обо­зна­ча­ю­щих фрагменты, в порядке, со­от­вет­ству­ю­щем IP-адресу.
7. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

 

46₁₆, 106₈, 1000101₂.
8. Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

 

59₁₀, 71₁₀, 81₁₀.

9. Сложить двоичные числа: 1110111+100011. Перемножить двоичные числа 110111*101

Часть С 
10. На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединён с нижним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно над горизонтальной стеной у её левого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше горизонтальной стены и левее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

---

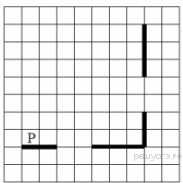
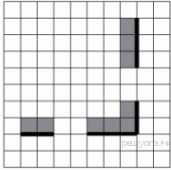
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.


Вариант 3

Часть A
1. В кодировке Unicode каждый символ кодируется двумя байтами. Текст, хранящийся на компьютере, содержит 1024 символов. Сколько Кб занимает этот текст?
1) 64

2) 6

3) 2

4) 4

2. В одной из ко­ди­ро­вок Unicode каж­дый сим­вол ко­ди­ру­ет­ся 16 битами. Опре­де­ли­те раз­мер сле­ду­ю­ще­го пред­ло­же­ния в дан­ной кодировке: Я па­мят­ник себе воз­двиг нерукотворный.

 

1) 304 байт

2) 38 байт

3) 76 бит

4) 608 бит
3. Скорость пе­ре­да­чи дан­ных через ADSL-соединение равна 512 бит/c. Пе­ре­да­ча файла через дан­ное со­еди­не­ние за­ня­ла 6 секунд. Опре­де­ли­те раз­мер файла в битах. В от­ве­те ука­жи­те одно число — раз­мер файла в Кбайт. Еди­ни­цы из­ме­ре­ния пи­сать не нужно.

1) 4096 байт

2) 38 байт

3) 4096 бит

4) 512 бит
Часть B

4. Доступ к файлу img.bmp, находящемуся на сервере pic.kz, осуществляется по протоколу http. Фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

 

A) img

Б) /

B) kz

Г) ://

Д) http

Е) .bmp

Ж) pic.

5 В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

 

Запрос	Количество страниц (тыс.)
фрегат & эсминец	500
фрегат | эсминец	4500
эсминец	2500

 

Сколько страниц (в тысячах) будет найдено по запросу фрегат?
6. На месте пре­ступ­ле­ния были об­на­ру­же­ны четыре об­рыв­ка бумаги. След­ствие установило, что на них за­пи­са­ны фрагменты од­но­го IP-адреса. Кри­ми­на­ли­сты обозначили эти фраг­мен­ты буквами А, Б, В и Г:

---

 

2.12	22	.30	5.121
А	Б	В	Г

 

Восстановите IP-адрес. В от­ве­те укажите по­сле­до­ва­тель­ность букв, обо­зна­ча­ю­щих фрагменты, в порядке, со­от­вет­ству­ю­щем IP-адресу.
7. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

 

67₁₆, 150₈, 1101000₂.

8. Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

 

59₁₀, 71₁₀, 81₁₀.

9. Сложить двоичные числа: 1110111+11011. Перемножить двоичные числа 11001*1111

Часть С
10. На бесконечном поле есть горизонтальная и вертикальная стены. Левый конец горизонтальной стены соединён с нижним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно над горизонтальной стеной у её правого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше горизонтальной стены и правее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).



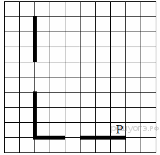
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.

---

Вариант 4

Часть A

1. В кодировке Unicode каждый символ кодируется двумя байтами. Текст, хранящийся на компьютере, содержит 8192 символов. Сколько Кб занимает этот текст?

1) 64

2) 16

3) 8

4) 4

2. В одной из ко­ди­ро­вок Unicode каж­дый сим­вол ко­ди­ру­ет­ся 16 битами. Опре­де­ли­те раз­мер сле­ду­ю­ще­го пред­ло­же­ния в дан­ной кодировке: Вознёсся выше он гла­вою не­по­кор­ной Алек­сан­дрий­ско­го столпа.

 

1) 118 бит

2) 472 байт

3) 944 бит

4) 59 байт
3. Скорость пе­ре­да­чи данных через ADSL-соединение равна 1024 бит/c. Пе­ре­да­ча файла через дан­ное соединение за­ня­ла 5 секунд. Опре­де­ли­те размер файла в килобайтах.

В от­ве­те укажите одно число — раз­мер файла в Кбайт. Еди­ни­цы измерения пи­сать не нужно.

1) 4096 байт

2) 5120 бит

3) 4096 бит

4) 5120 байт


Часть B

4. Доступ к файлу book.txt, находящемуся на сервере bibl.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

 

A) ://

Б) book.

B) bibl

Г) txt

Д) .ru

Е) http

Ж)/

5. В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

Запрос	Количество страниц (тыс.)
шахматы | теннис	7770
теннис	5500
шахматы & теннис	1000

 

 

Сколько страниц (в тысячах) будет найдено по запросу шахматы
6. Миша за­пи­сал IP-адрес школь­но­го сервера на лист­ке бумаги и по­ло­жил его в кар­ман куртки. Ми­ши­на мама слу­чай­но постирала курт­ку вместе с запиской. После стир­ки Миша об­на­ру­жил в кар­ма­не четыре об­рыв­ка с фраг­мен­та­ми IP-адреса. Эти фраг­мен­ты обозначены бук­ва­ми А, Б, В и Г:

 

17	.44	4.144	9.13
А	Б	В	Г

 

Восстановите IP-адрес. В от­ве­те укажите по­сле­до­ва­тель­ность букв, обо­зна­ча­ю­щих фрагменты, в порядке, со­от­вет­ству­ю­щем IP-адресу.

---

7. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

 

81₁₆, 203₈, 1111111₂.

8. Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

 

100₁₀, 90₁₀, 80₁₀.

9. Сложить двоичные числа: 1110101+110111. Перемножить двоичные числа 11010*1111
Часть С

10. На бесконечном поле есть горизонтальная и вертикальная стены. Левый конец горизонтальной стены соединён с верхним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно под горизонтальной стеной у её правого конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно ниже горизонтальной стены и правее вертикальной стены. Проходы должны остаться незакрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого рисунка Робот должен закрасить следующие клетки (см. рисунок).



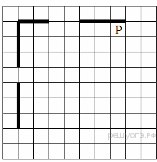
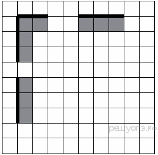
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен. Алгоритм может быть выполнен в среде формального исполнителя или записан в текстовом редакторе. Сохраните алгоритм в текстовом файле.

---

Смотрите также файлы

• В егер сын ділетті болса, ескеруге тырысамын.docx

• Задача в статье 582 указано, что узуфруктуарий имеет право пользоваться всеми плодами (естественными, промышленными) На который он имеет узуфрукт.docx

• Практическая работа 3 (Часть 1) Раздел программы 1 Планирование и управление образовательным процессом.doc

• Фин. Вычисления 1.doc

• Влияние и оценка личностных и деловых качеств фармацевтических специалистов при подборе персонала в аптечных организациях на примере ооо Омега аптека 96.doc