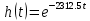ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

Предмет:

Теоретические Основы Электротехники.

Контрольная работа № 1




Выполнил:

вариант № 15.

Проверил: ст. преподаватель Степанова А.Г.









Решение.

Определим номиналы элементов цепи:

















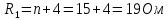
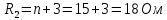
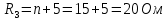
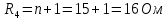
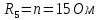
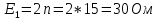
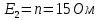
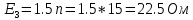
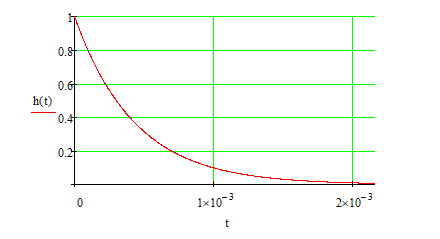
Обозначим условно-положительные направления токов ветвей, пронумеруем узлы и обозначим направления обхода независимых контуров цепи.



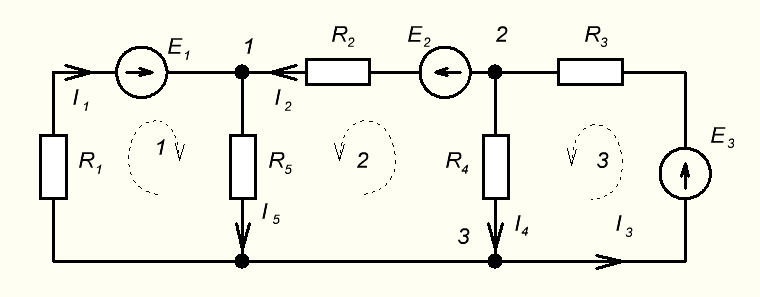
В цепи у=3 узла, и=5 ветвей и к=3 независимых контура. Составляем у-1=2 уравнения по 1му закону Кирхгофа для узлов 1-2 и к=3 уравнения по 2му закону Кирхгофа для обозначенных на схеме контуров.

---

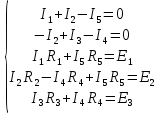
Решение системы уравнений в Mathcad:





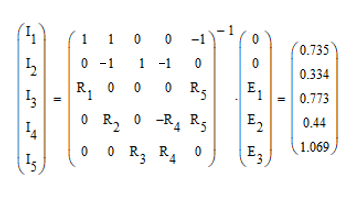
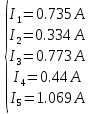
Составляем баланс мощностей:





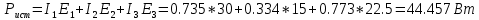
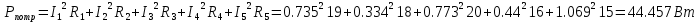
Баланс сошелся.









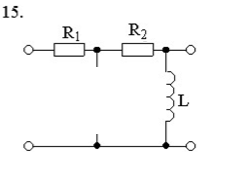
Решение.

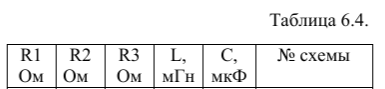
Определим параметры цепи:











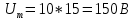
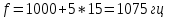
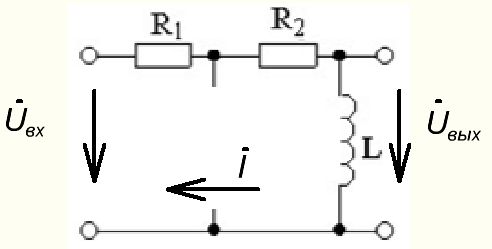
1. Расчет цепи при гармоническом воздействии



Комплексная амплитуда действующего значения входного напряжения:



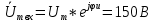
Комплекс действующего значения входного напряжения:



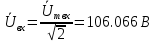
Комплексное сопротивление цепи:



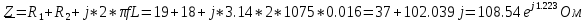
Комплексная амплитуда тока в цепи:



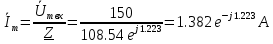
Комплекс действующего значения тока:



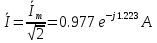
Мгновенное значение тока в цепи:



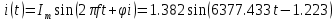
Комплексная амплитуда выходного напряжения:



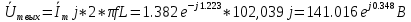
Мгновенное значение выходного напряжения:

---

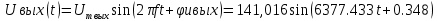
Мощность источника:







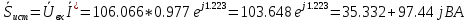
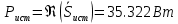
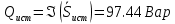
Мощность нагрузки:





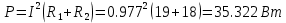
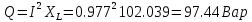
Т.к. мощности источника и нагрузки равны, то баланс сошелся.

2. Выражение для комплексной передаточной функции





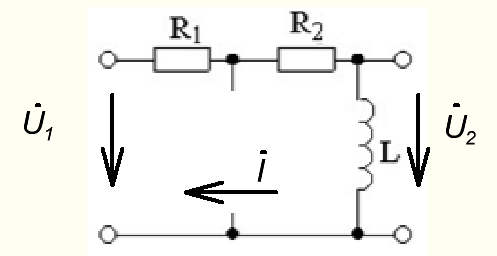
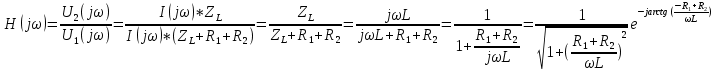
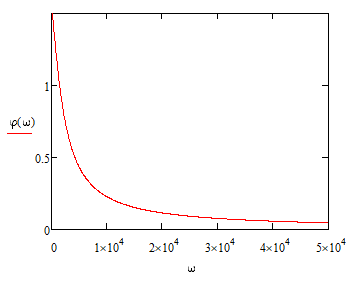
АЧХ:





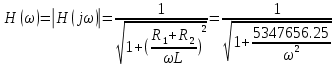
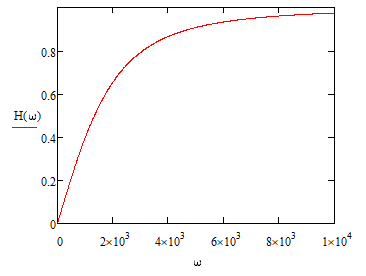
ФЧХ:





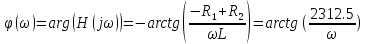
3. Операторная передаточная функция цепи:

Получим выражение подстановкой 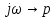в выражение комплексной передаточной функции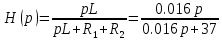



Определим операторным методом импульсную характеристику цепи.

Операторное изображение дельта функции:



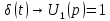
Операторное изображение отклика цепи на воздействие дельта функции:



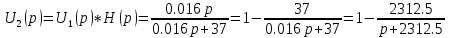
Используя таблицу преобразования Лапласа получим оригинал, равный импульсной характеристике цепи:





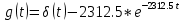
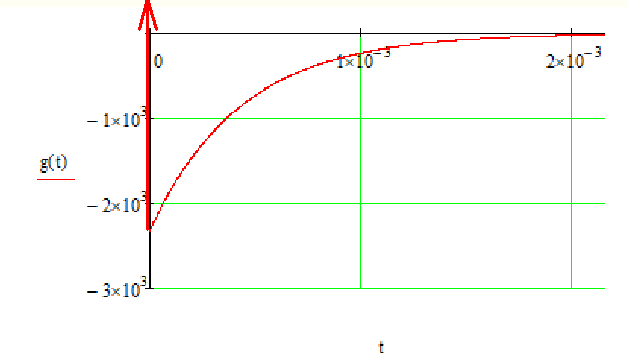
Операторное изображение функции хевисайда:



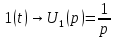
Операторное изображение отклика цепи на воздействие функции хевисайда:

---

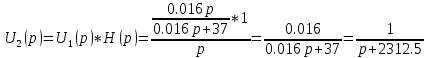
Используя таблицу преобразования Лапласа получим оригинал, равный переходной характеристике цепи:

---

Смотрите также файлы

• Иды и формы землеустроительной документации.pdf

• Эксплуатационные свойства подвижного состава.pptx

• визуализация как средство формирования коммуникативной компетентности учащихся.doc

• I. сущность конфликта поколений.rtf

• Государственное бюджетное профессиональное образовательное учреждение уренский индустриальноэнергетический техникум.docx