Файл: Введение 1 Цепные дроби 2 Подходящие дроби 3 Представление рациональных чисел цепными дробями 3 Разложение действительного иррационального числа в правильную бесконечную цепную дробь 4.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 192
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Здесь 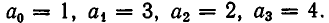 Вычисление будет состоять из следующих шагов:
Вычисление будет состоять из следующих шагов:
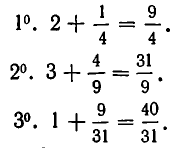
Ответ: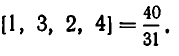
Обращение конечной цепной дроби в обыкновенную — всегда выполнимая задача. На это потребуется не более чем n шагов, каждый из которых состоит в сложении двух чисел: целого числа и правильной дроби.
Если в непрерывной дроби возьмём несколько звеньев с начала, отбросив все остальные, и составленную
ими непрерывную дробь обратим в обыкновенную, то получим так называемую подходящую дробь. Первая подходящая дробь получится, когда возьмём одно первое звено: вторая — когда возьмём два первых звена, и т. д. Таким образом, для непрерывной дроби:
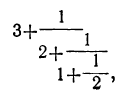
первая подходящая дробь есть ;
вторая „ „ „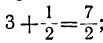
третья „ „ „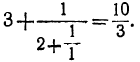
Четвёртая подходящая дробь представит в этом примере точную величину непрерывной дроби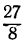 .
.
Когда в непрерывной дроби нет целого числа, то первая подходящая дробь есть 0.
Составим для непрерывной дроби ( a a₁, a₂,…, ) первые три подходящие дроби:
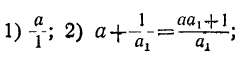
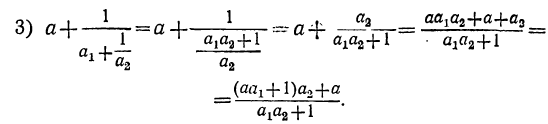
Сравнивая третью подходящую дробь с двумя первыми, заметим, что числитель третьей подходящей дроби получится, если числитель второй подходящей дроби умножим на соответствующее частное (т. е. на α₂) и к полученному произведению прибавим числитель первой подходящей дроби
; знаменатель третьей подходящей дроби получится подобным же образом из. знаменателей предыдущих двух подходящих дробей.
Докажем, что этот закон применим ко всякой подходящей дроби, следующей за третьей, т. е. мы докажем, что вообще числитель (n+1)-й подходящей дроби получится, если числитель n-й подходящей дроби умножим на соответствующее частное (т. е. на ) и произведение сложим с числителем (n— 1)-й подходящей дроби, и что знаменатель (n+l)-й подходящей дроби подобным же способом получится из знаменателей n-й и (n — 1)-й подходящих дробей. Употребим доказательство от n к (n+1), т. е. докажем, что если этот закон применим к n-й подходящей дроби, то он применим и к (n+1)-й подходящей дроби.
Обозначим первую, вторую, третью и т. д. подходящие дроби последовательно через
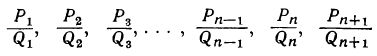
и заметим, что соответствующие им частные будут:
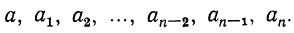
Допустим, что верны равенства:
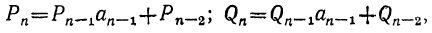 (1)
(1)
и, следовательно:
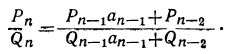 (2)
(2)
Требуется доказать, что в таком случае и
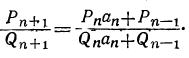 (3)
(3)
Из сравнения двух подходящих дробей:
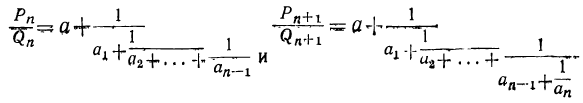
усматриваем, что (n+1)-я подходящая дробь получится из n-й, если в последней заменим число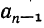 на сумму
на сумму 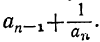
Поэтому равенство (2) даёт:
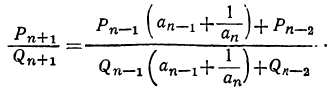
Раскрыв скобки и умножив оба члена дроби на , получим:
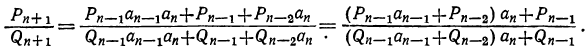
Приняв во внимание равенство (1), можем окончательно написать:
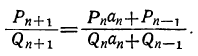
Это и есть равенство (3), которое требовалось доказать.
Таким образом, если доказываемый закон верен для n-й подходящей дроби, то он будет верен и для (n+l)-й подходящей дроби. Но мы непосредственно видели, что он верен для третьей подходящей дроби; следовательно, по доказанному, он применим для четвёртой подходящей дроби; а если для четвёртой, то и для пятой и т. д.
Пользуясь этим законом, составим все подходящие дроби для следующего примера:
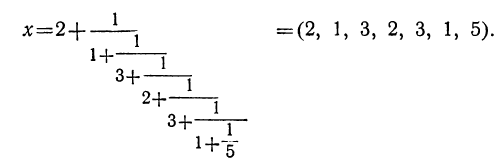
Вычисления всего удобнее расположить так:
Первые две подходящие дроби найдём непосредственно, это будут и . Остальные подходящие дроби получим, основываясь на доказанном законе. Для памяти размещаем в верхней строке целые частные с третьего до последнего.
Теорема:
Точное значение непрерывной дроби заключается между двумя последовательными подходящими дробями, причём оно ближе к последующей, чем к предыдущей.
Доказательство:
Пусть имеем непрерывную дробь:
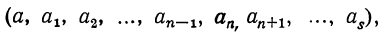
точную величину которой обозначим через А. Возьмём какие-нибудь три последовательные подходящие дроби:
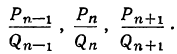
По доказанному, имеем:
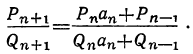
Если в правую часть этого равенства мы вместо подставим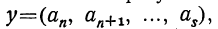 , то в левой части получим точную величину А непрерывной дроби, значит:
, то в левой части получим точную величину А непрерывной дроби, значит:
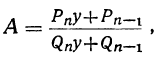
откуда:
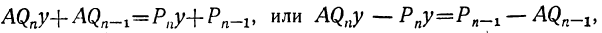
и значит:
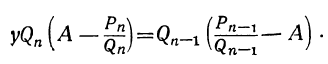
Из последнего равенства можем вывести два следующих заключения:
1) Так как числа у, и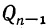 положительные, то разности, стоящие внутри скобок, должны быть одновременно положительны или одновременно отрицательны; значит:
положительные, то разности, стоящие внутри скобок, должны быть одновременно положительны или одновременно отрицательны; значит:
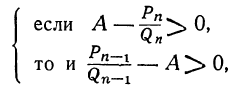 или
или 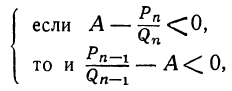
т.е.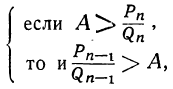 или
или 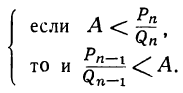
Следовательно, А заключено между всякими двумя последовательными подходящими дробями.
2) Так как у>1 и >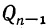 , причём числа и
, причём числа и 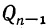
положительные, то из того же равенства выводим: абсолютная величина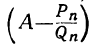 меньше абсолютной величины
меньше абсолютной величины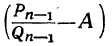 .
.
Отсюда следует, что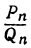 ближе к А, чем
ближе к А, чем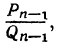 , что и требовалось доказать.
, что и требовалось доказать.
Замечание:
Так как, очевидно, A>а, т. е.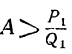 , то
, то
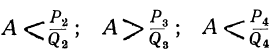 и т. д.
и т. д.
Точное значение непрерывной дроби более всякой подходящей дроби нечётного порядка и менее всякой подходящей дроби чётного порядка.
Теорема:
Разность между двумя рядом стоящими подходящими дробями равна + 1, делённой на произведение знаменателей этих подходящих дробей.
Доказательство:
Так как
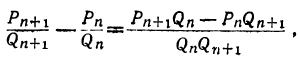
то очевидно, что знаменатель этой разности удовлетворяет требованию теоремы. Остаётся доказать, что числитель равен ±1.
Так как
Pn+1=Pnαn+Pn-1 и Q,,+ι=Qnαn+Qn-ι,
то
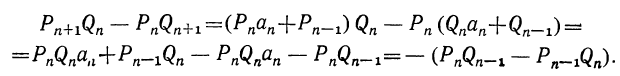
Выражение, стоящее в скобках, представляет собой числитель P P —
дроби, которая получится от вычитания из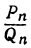 дроби
дроби 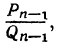
Следовательно, мы доказали, что абсолютная величина числителя дроби, получаемой от вычитания
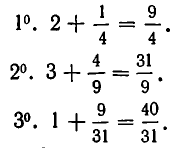
Ответ:
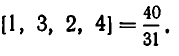
Обращение конечной цепной дроби в обыкновенную — всегда выполнимая задача. На это потребуется не более чем n шагов, каждый из которых состоит в сложении двух чисел: целого числа и правильной дроби.
-
Подходящие дроби
Если в непрерывной дроби возьмём несколько звеньев с начала, отбросив все остальные, и составленную
ими непрерывную дробь обратим в обыкновенную, то получим так называемую подходящую дробь. Первая подходящая дробь получится, когда возьмём одно первое звено: вторая — когда возьмём два первых звена, и т. д. Таким образом, для непрерывной дроби:
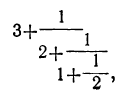
первая подходящая дробь есть ;
вторая „ „ „
третья „ „ „
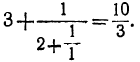
Четвёртая подходящая дробь представит в этом примере точную величину непрерывной дроби
Когда в непрерывной дроби нет целого числа, то первая подходящая дробь есть 0.
Составим для непрерывной дроби ( a a₁, a₂,…, ) первые три подходящие дроби:
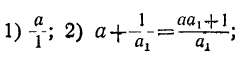
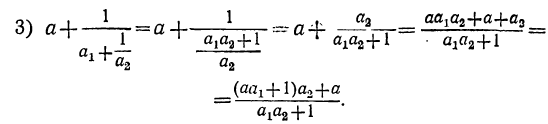
Сравнивая третью подходящую дробь с двумя первыми, заметим, что числитель третьей подходящей дроби получится, если числитель второй подходящей дроби умножим на соответствующее частное (т. е. на α₂) и к полученному произведению прибавим числитель первой подходящей дроби
; знаменатель третьей подходящей дроби получится подобным же образом из. знаменателей предыдущих двух подходящих дробей.
Докажем, что этот закон применим ко всякой подходящей дроби, следующей за третьей, т. е. мы докажем, что вообще числитель (n+1)-й подходящей дроби получится, если числитель n-й подходящей дроби умножим на соответствующее частное (т. е. на ) и произведение сложим с числителем (n— 1)-й подходящей дроби, и что знаменатель (n+l)-й подходящей дроби подобным же способом получится из знаменателей n-й и (n — 1)-й подходящих дробей. Употребим доказательство от n к (n+1), т. е. докажем, что если этот закон применим к n-й подходящей дроби, то он применим и к (n+1)-й подходящей дроби.
Обозначим первую, вторую, третью и т. д. подходящие дроби последовательно через
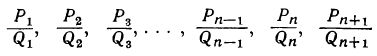
и заметим, что соответствующие им частные будут:
Допустим, что верны равенства:
и, следовательно:
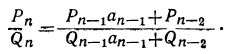 (2)
(2)Требуется доказать, что в таком случае и
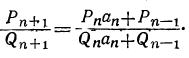 (3)
(3)Из сравнения двух подходящих дробей:
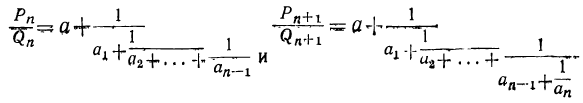
усматриваем, что (n+1)-я подходящая дробь получится из n-й, если в последней заменим число
Поэтому равенство (2) даёт:
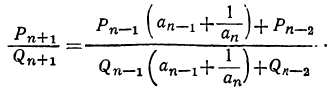
Раскрыв скобки и умножив оба члена дроби на , получим:
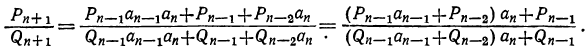
Приняв во внимание равенство (1), можем окончательно написать:
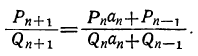
Это и есть равенство (3), которое требовалось доказать.
Таким образом, если доказываемый закон верен для n-й подходящей дроби, то он будет верен и для (n+l)-й подходящей дроби. Но мы непосредственно видели, что он верен для третьей подходящей дроби; следовательно, по доказанному, он применим для четвёртой подходящей дроби; а если для четвёртой, то и для пятой и т. д.
Пользуясь этим законом, составим все подходящие дроби для следующего примера:
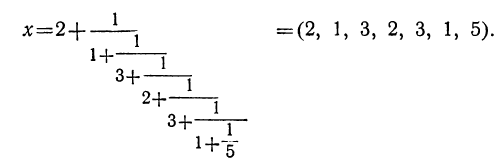
Вычисления всего удобнее расположить так:
| | | 3 | 2 | 3 | 1 | 5 |
| 2 | 3 | 11 | 25 | 86 | 111 | 641 |
| 1 | 1 | 4 | 9 | 31 | 40 | 231 |
Первые две подходящие дроби найдём непосредственно, это будут и . Остальные подходящие дроби получим, основываясь на доказанном законе. Для памяти размещаем в верхней строке целые частные с третьего до последнего.
Теорема:
Точное значение непрерывной дроби заключается между двумя последовательными подходящими дробями, причём оно ближе к последующей, чем к предыдущей.
Доказательство:
Пусть имеем непрерывную дробь:
точную величину которой обозначим через А. Возьмём какие-нибудь три последовательные подходящие дроби:
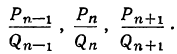
По доказанному, имеем:
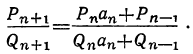
Если в правую часть этого равенства мы вместо подставим
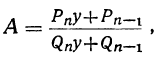
откуда:
и значит:
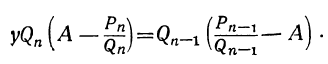
Из последнего равенства можем вывести два следующих заключения:
1) Так как числа у, и
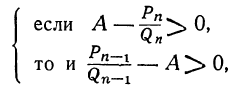 или
или 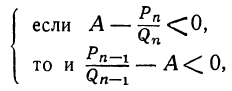
т.е.
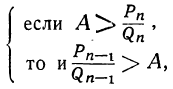 или
или 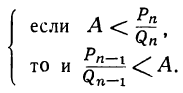
Следовательно, А заключено между всякими двумя последовательными подходящими дробями.
2) Так как у>1 и >
положительные, то из того же равенства выводим: абсолютная величина
Отсюда следует, что
Замечание:
Так как, очевидно, A>а, т. е.
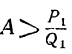 , то
, то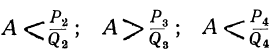 и т. д.
и т. д.Точное значение непрерывной дроби более всякой подходящей дроби нечётного порядка и менее всякой подходящей дроби чётного порядка.
Теорема:
Разность между двумя рядом стоящими подходящими дробями равна + 1, делённой на произведение знаменателей этих подходящих дробей.
Доказательство:
Так как
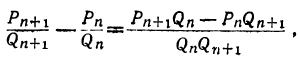
то очевидно, что знаменатель этой разности удовлетворяет требованию теоремы. Остаётся доказать, что числитель равен ±1.
Так как
Pn+1=Pnαn+Pn-1 и Q,,+ι=Qnαn+Qn-ι,
то
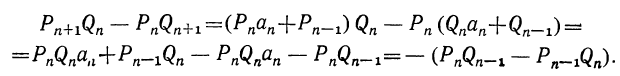
Выражение, стоящее в скобках, представляет собой числитель P P —
дроби, которая получится от вычитания из
Следовательно, мы доказали, что абсолютная величина числителя дроби, получаемой от вычитания