К качественным графикам относятся графики изменения среднего значения содержания золота по отдельной разведочной линии и графики площадного содержания (производительности). Вначале строят графики изменения содержания по каждой разведочной линии. Критерием правильности проведенной разведки и полученных данных является примерно одинаковое содержание золота по разведочным линиям, так как вероятность перехода золота в свободное состояние, т.е. освобождение его из коренной породы, на всем пути движения кусков породы одинакова. Таким образом, средние значения содержаний по каждой разведочной выработке не должны меняться в широких пределах. Если это наблюдается, следовательно, существуют ошибки в разведке россыпи.

Запасы золота в россыпи, а также промышленный контур месторождения определяют по плану производительности россыпи. Под производительность россыпи в конкретной разведочной выработке понимают значение Р = l · с · 1 м2 · γ (l – мощность россыпи по разведочной выработке; с – содержание полезного компонента; γ – объемный вес).

Планпроизводительности россыпи строятв следующем порядке:

1)по каждой разведочной выработке определяют значение производительности залежи песков Р;

2)строят графики изменения производительности по отдельным разведочным линиям;

3)находят на графике точки, соответствующие целочисленным отметкам Р и сносят их на линии разреза;

4)точки с одинаковыми значениями производительности соединяют плавными линиями.

Этот график дает наглядное представление о распределении металла по россыпи.

В процессе отработки россыпи производят систематическую съемку отработанных площадей и составляют геометрические графики учета работы драг. Сопоставление фактических и первоначальных графиков позволяет определить степень их соответствия друг другу, установить потери в различного рода целиках, определить места, где остались неотработанные участки россыпи.
Решение горно-геометрических задач в проекции с числовыми отметками

Все решаемые задачи в геометрии недр делятся на два вида: позиционные и метрические. К позиционным задачам относятся изображение формы залежи, горных выработок, поверхности земли, кровли и почвы залежи и другие. К 

---

метрическим задачам относятся определение параметров и элементов залегания залежи в горном массиве. Установление линий пересечения залежи с различными слоями горных пород, определение различных геометрических параметров и размеров различных тектонических нарушений, смещений и другие сведений. Метрические задачи решают различными аналитическими и геометрическими методами. Важными условиями при графическом изображении различных объектов являются:

-наглядность – это по графическому изображению (на планах или разрезах) без особого труда представить пространственную модель горно-геологического объекта. Легко определить параметры и элементы залежи, и детально распознать внутреннее устройство объекта с наименьшим перекрытием.

–простата построения – это выбор правильной системы изображения различных объектов на плоскости проекции для построения планов и разрезов.

- удобоизмеряемость – это на планах и разрезах, где выполнены изображения объекта, можно легко производить измерения параметров и элементов залегания для решения метрических задач с определенной степенью точности.

-динамичность – это возможность систематического пополнения маркшейдерских графических материалов в соответствии с развитием горных и разведочных работ.

контрастность – это возможность четкого чтения изображения и отбора необходимой информации для работы на специальных приборах и компьютерах.

Выбор масштаба графического изображения объекта является важным условием при решении позиционных и метрических задач.

Масштаб чертежа (плана или разреза) равна:

M= а/Д,

где а – максимальная ошибка графических построений, равная 0,2-0,3 мм; Д – необходимая точность определения исходного расстояния, мм.

Пример 1. Пусть длина l= 120 м. Относительная погрешность определения 1:1000. Установить масштаб чертежа.

Д = 120/1000 = 0,12 м = 120 мм.

М = 0,3/120 = 1/400 или ближайший масштаб по ГОСТу 1:500.

Для графического изображения различных объектов применяют два метода проекций: центральный и параллельный.

Сущность центрального или конического метода проекций заключается в следующем: например, возьмем горизонтальную плоскость Н и точку S в пространстве, которую назовем полюсом и не принадлежащая плоскости 

---

Н. Возьмем некоторую точку А, находящуюся между полюсом S и плоскостью Н (,а). Проведем из полюса S через точку А некоторый луч до пересечения его с плоскостью Н и получим на ней точку а.

Здесь плоскость Н называют плоскостью проекций, точку S - центром проецирования, точку а - центральной проекцией точки А на плоскости Н, луч SА - проецирующим лучом.

С помощью этого метода можно спроецировать на плоскость прямую, кривую, любой геометрический объект.. Для этого достаточно найти несколько проекций точек, принадлежащих заданной прямой (6) или кривой (в) линии или другой геометрической формы (,в) и соединить их.



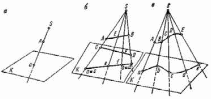
Центральный метод проецирования: а- точки; б-прямой; в- кривой.

Параллельный метод проецирования является частным случаем центрального проецирования. Полученные с помощью такого метода проецирования проекции называются параллельными



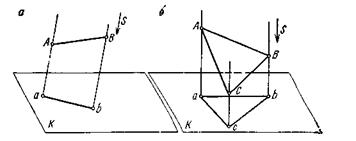
а- прямой; б- геометрической фигуры.

При параллельном проектировании прямой АВ или плоскости АВС на горизонтальную плоскость Н, то получим их проекции без искажения. Параллельный метод проецирования широко применяется в практике. При этом методе графическое отображение изучаемого объекта учитывают два основных требования: наглядность и удобоизмеряемость.

Если же проецирующие лучи направить перпендикулярно к плоскости проекций то получим прямоугольный метод проецирования или ортогональный. Когда проецирующие лучи направлены под острым углом к плоскости проекций, получаем косоугольный метод проецирования.

---

Проекции с числовыми отметками. Сущность метода проекций с числовыми отметками заключается в том, что на некоторую плоскость, называемую плоскостью проекций, ортогонально проектируются точки, принадлежащие некоторым элементам или пространственному телу. На плоскости проекций получают изображение проектируемых элементов или тела в двух измерениях. Третьим измерением являются числовые отметки точек.

Числовой отметкойназывают расстояние по нормали от проектируемой точки до плоскости проекций. За основную плоскость проекций в практике чаще всего применяется горизонтальная.

На рис.6 показано изображение точек в проекциях с числовыми отметками. В пространстве взяты произвольные точки А и В и горизонтальная плоскость Н. Точка С взята на плоскости и ее числовая отметка равна нулю. Проекции точки   , В провести перпендикулярные к плоскости линии до пересечения с ней, то получим прямоугольные проекции точек а, b на плоскости Н. Нетрудно видеть, что точка С совпадает со своей проекцией с₀, и лежит на плоскости проекции. Числовые отметки точек, расположенных над плоскостью проекций, считаются положительными, ниже плоскости -отрицательными. Знак минус пишется только у отрицательных числовых отметок.



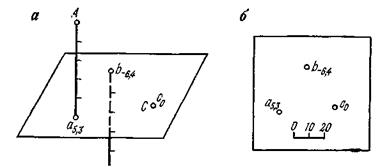
Рис.6. Проецирование точек на горизонтальную плоскость проекций:

а - точки А и В расположены вне плоскости проекций ; б - точка С на плане.

Часто некоторые объекты проецируются на вертикальную плоскость V (рис.7). На рис. 7 показан способ проецирования точек Д и Е на вертикальную плоскость. При этом отрицательные отметки имеют точки, расположенные за плоскостью проекций.

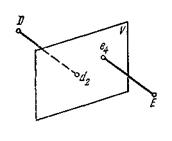Проецирование точек на вертикальную плоскость проекций.

Если горизонтальную или вертикальную плоскости проекций принимают за любую условную плоскость, то числовые отметки называют условными отметками(относительными).

Проекции точек и прямых линий.В практике часто некоторые выработки принимают за точку и прямую линию. Это

---

скважины и горных выработки, линии простирания и падения залежей полезного ископаемого, горных пород и другие.

Отрезок прямой на плане в проекциях с числовыми отметками может быть задан координатами двух точек а_16,2 и в_48,2 прямой (ав) (рис. 8,а), координатами одной точки с_10,5 и направлением прямой под дирекционным углом α (рис. 8,6) и углом падения прямой β (рис. 8,в).



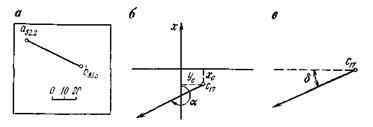
Рис. 8. Изображение отрезка прямой линии в проекциях с числовыми отметками.

Углом направления α прямой называется угол между северным направлением оси х и направлением прямой в сторону ее понижения, отсчитываемый по ходу часовой стрелки. Углом наклона β называется угол падения прямой к горизонту. В зависимости от знака угла наклона различают угол восстания (+β) и угол падения (-β) . Углы восстания и падения численно равны. На рис. 9 показана прямая АВ. Отрезок СВ этой прямой имеет угол падения δ, а отрезок СА этой же прямой - угол восстания, равный также δ.



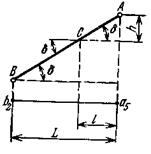
Рис. 9. К определению угла наклона прямой

Тангенс угла наклона прямой называется уклоном прямой, т.е.   . Проекция прямой на горизонтальную плоскость Н между двумя точками называется заложением l.

При решении различного характера задач в геологии, маркшейдерии и горном деле пользуются уклоном прямой, заложением и высотой сечения h этой прямой.

Градуированием прямойназывается определение на проекции прямой точек с дискретными (или кратными) числами, равные высоте сечения. Например, кратными числами могут быть 0,5, 1, 2,5 м и т.д.

Градуирование прямой может быть выполнено на глаз, с помощью трафарета или аналитическими способами. Аналитический способ градуирования прямой заключается в следующем: Пусть на рис. 10 дан в плане отрезок a₁₆b₂₅.

---

Смотрите также файлы

• Вопросы к диф зачёту по модулю пм 04 (пм 07) Выполнение работ по профессии Мл мс по уходу.doc

• Cabron Подписаться 789 подписчиков Войти 6 Финансовый менеджмент 9 октября 2022.docx

• Агрегатные состояния вещества.docx

• 1 вариант.docx

• .docx