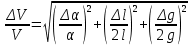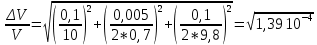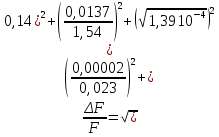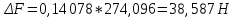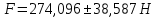Файл: Отчет по лабораторной работе исследование соударения шарика со стенкой.docx
Добавлен: 12.01.2024
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Кузбасский государственный технический университет
имени Т. Ф. Горбачева»
Кафедра физики
 Отчет
Отчетпо лабораторной работе №
«ИССЛЕДОВАНИЕ СОУДАРЕНИЯ ШАРИКА СО СТЕНКОЙ»
Выполнил ст. группы
________________________________
(Ф.И.О.)
Преподаватель
________________________________
(Ф.И.О.)
| | Дата | Роспись |
| Допуск | | |
| Отчет | | |
Цель работы: определение коэффициента восстановления, продолжительности удара и средней силы взаимодействия шарика со стенкой
Приборы и принадлежности: на экране изображена экспериментальная установка. В ней имеется металлическая стенка, об которую может ударяться металлический шарик, подвешенный на тонкой металлической нити
Схема установки
 |
| Рис.1. Основное окно программы и схема экспериментальной установки |
Основные расчетные формулы
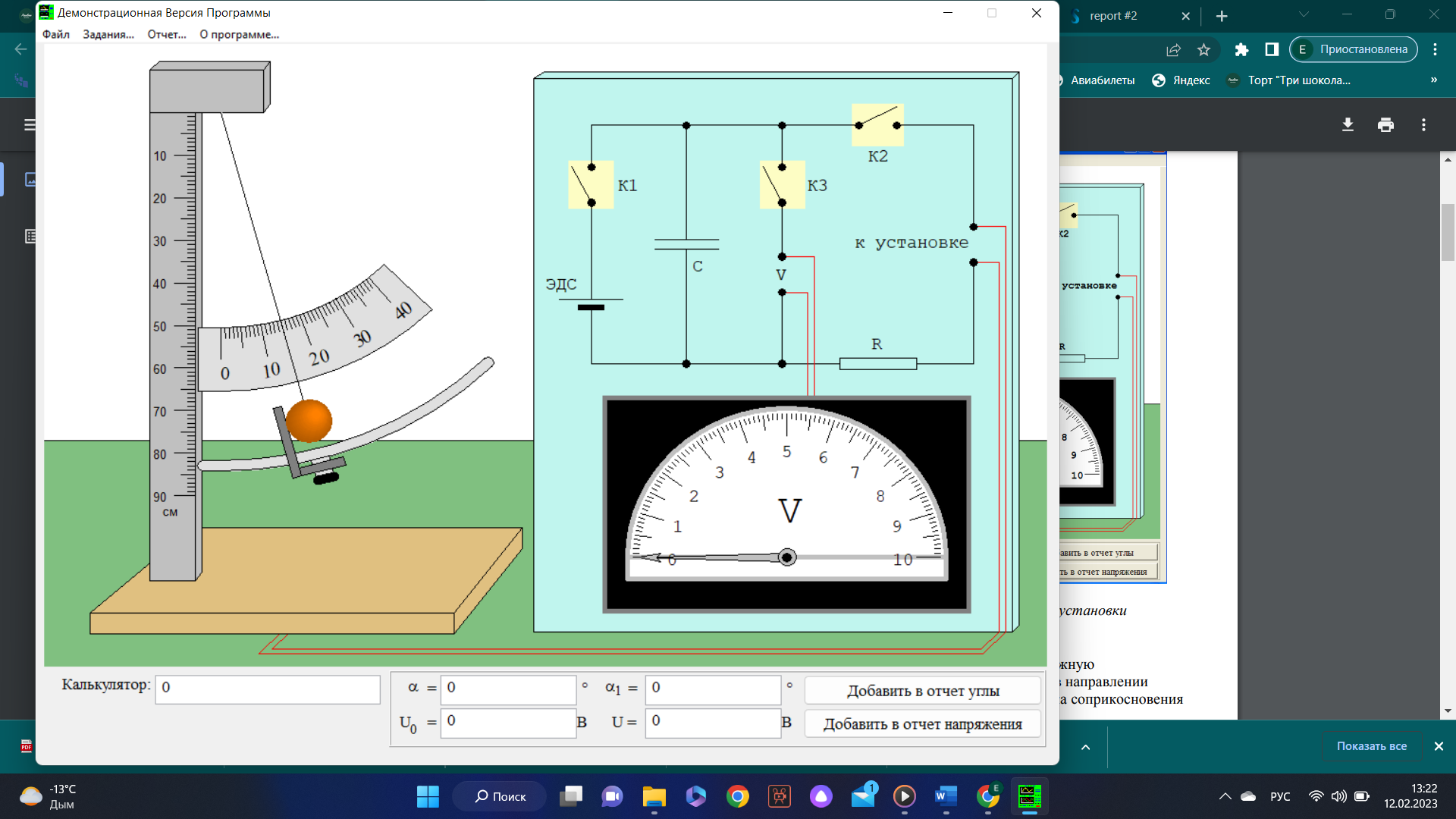
Коэффициент восстановления. V – скорость шарика до удара; V1 – скорость шарика после удара. Упругие свойства системы удобно характеризовать коэффициентом восстановления
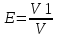 (2.2)
(2.2)Очевидно,
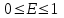
, где значения V1 и V соответствуют неупругому и абсолютно упругому удару. Фактически
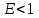 .
.Скорость шарика в работе определяется косвенным образом. Шарик подвешен на длинной нити так, что в положении равновесия соприкасается с плитой.
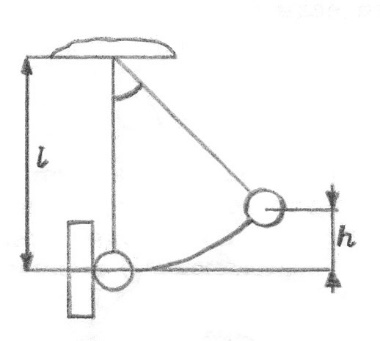 |
При отклонении нити на угол α центр тяжести шарика поднимается на высоту
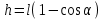 (2.3)
(2.3)Из закона сохранения механической энергии следует:
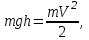 (2.4)
(2.4)где V – скорость шарика в нижней точке. Из (2.4) и (2.3) получаем
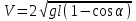
или
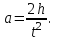 (2.5)
(2.5)Зная начальный угол отклонения шарика α, можно из (2.5) найти его скорость V в начале соударения. А скорость шарика V1 в конце соударения:
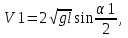 (2.6)
(2.6)где α1 – максимальный угол отклонения после удара. Тогда из (2.5) и (2.6) получаем соотношение для расчета коэффициента восстановления
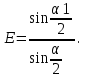 (2.7)
(2.7)Время соударения. Для определения продолжительности удара в работе используется косвенный метод. Известно, что если заряженный конденсатор емкостью С замкнуть на сопротивление R, то напряжение на нем уменьшается по экспоненциальному закону:
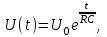 (2.8)
(2.8)где t – время,
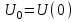 - начальное напряжение.
- начальное напряжение.В лабораторной установке замыкание цепи, через которую разряжается конденсатор, происходит при контакте шарика с плитой. В результате напряжение на конденсаторе после удара оказывается меньше, чем до удара. Измерив
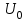 и
и 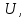 можно из (2.8) найти длительность удара
можно из (2.8) найти длительность удара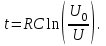 (2.9)
(2.9)Электрическая схема
, используемая в работе.
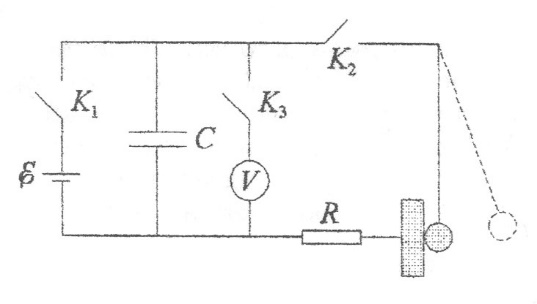
При замыкании ключа К1 конденсатор С заряжается от батареи Е. Напряжение на конденсаторе измеряется вольтметром V при замыкании ключа К3. Ключ К2 служит для временного замыкания цепи разряда конденсатора. Шарик, подвешенный на металлической нити, при контакте с плитой выполняет роль ключа, замыкающего цепь в течение удара.
Зная длительность удара t, можно из второго закона Ньютона найти среднюю силу F взаимодействия шарика со стенкой.
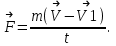 (2.10)
(2.10)Учитывая, что
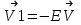 , получаем
, получаем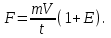 (2.11)
(2.11)Определение коэффициента восстановления E
Отклонили шарик на угол α=15°. Затем, освободив шарик, зарегистрировали угол α1 максимального отклонения. Занесли значения углов в таблицу 1. Измерения провели 5 раза.
Провели опыт для углов α =10° и α =5° для каждого угла сделали 5 измерений(таблица 1).
Таблица 1. Значения углов.
| № | α1(α=15o) | α2(α=10o) | α3(α=5o) |
| 1 | 7,0 | 5,0 | 3,0 |
| 2 | 7,0 | 5,0 | 3,0 |
| 3 | 6,0 | 5,5 | 3,5 |
| 4 | 8,0 | 5,0 | 3,0 |
| 5 | 7,0 | 5,0 | 3,5 |
| Средние | 7,0 | 5,1 | 3,2 |
Рассчитали для каждого из углов коэффициент восстановления E:
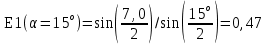
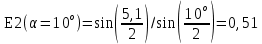
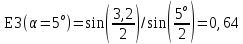
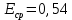
Определение продолжительности удара t
Отклонили шарик на угол α =15°. Нажав на ключ K1, зарядили конденсатор от источника напряжения. Затем подключили к конденсатору вольтметр, нажав на ключ K3. Измерили начальное напряжение U0 на конденсаторе и отключили вольтметр, выключив K3(см. таблицу 2).
Подсоединили конденсатор к шарику через проводящую нить, включив ключ K2. После чего освободили шарик.
Во время удара шарика о стенку происходит постепенный разряд конденсатора. Скорость разряда задаётся значением ёмкости C=
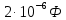 и величиной балластного резистора R= (220±0,1) Ом. Сразу после удара ключ K2 автоматически выключится. После этого измерили остаточное напряжение U на конденсаторе и занесли его в таблицу 2. Провели опыт 5 раз для углов 10 и 5.
и величиной балластного резистора R= (220±0,1) Ом. Сразу после удара ключ K2 автоматически выключится. После этого измерили остаточное напряжение U на конденсаторе и занесли его в таблицу 2. Провели опыт 5 раз для углов 10 и 5. Таблица 2.
| № | Uo, B | U(α=15o) | U(α=10o) | U(α=5o) |
| 1 | 8 | 6,8 | 6,6 | 6,4 |
| 2 | 8 | 6,7 | 6,6 | 6,4 |
| 3 | 8 | 6,8 | 6,6 | 6,4 |
| 4 | 8 | 6,7 | 6,5 | 6,4 |
| 5 | 8 | 6,8 | 6,5 | 6,4 |
| Средние | 8 | 6,76 | 6,56 | 6,4 |
Рассчитаем значения t:
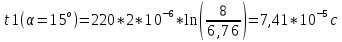
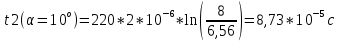
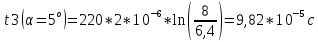
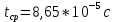
Найдем скорости шарика в нижней точке
g=9,8м/с2 l=(0,700±0,005)м
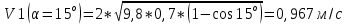
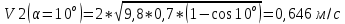
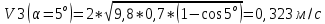
Найдем среднюю силу взаимодействия шарика со стенкой:
m=(0,02300±0,00002)кг
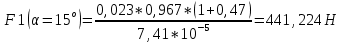
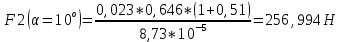
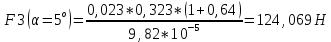
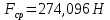
Расчет погрешностей E, F, V, t
Для α=10.
(1)
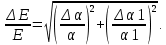
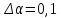
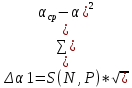
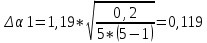
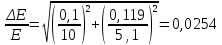
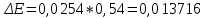
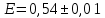
(2)
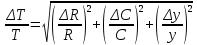 , где
, где 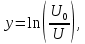
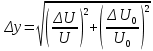
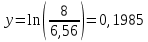
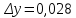
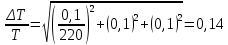
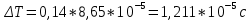
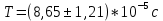
(3)
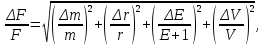 где
где