ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 45
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Введение
Фазовые переходы второго рода. В этом случае плотность и внутренняя энергия не меняются, вследствие чего визуально такой фазовый переход может не наблюдаться.
Если система является однокомпонентной, то понятие фазы совпадает с понятием агрегатного состояния вещества; таким образом, превращения первого рода являются более «очевидными»: они сопровождаются выделением тепла и изменением физических характеристик (формы, объема). А что происходит при фазовых переходах второго рода?
Фазовые переходы второго рода связаны с изменением свойств внутренней симметрии вещества. Примеры — переход в ферромагнитное состояние, в антиферромагнитное, в сверхпроводящее состояние, для гелия — в сверхтекучее; многие переходы между кристаллическими модификациями. При фазовом переходе второго рода нет теплоты перехода, нет скачка объема, но есть скачки теплоемкости, коэффициента сжимаемости и т.п.
Теория самосогласованного поля и теория фазовых переходов II-го рода Ландау. Параметр порядка. Микроскопическая теория магнитного фазового перехода в приближении самосогласованного поля. Уравнения Клапейрона–Клаузиуса и Эренфеста. Флуктуационная теория Орнштейна–Цернике вблизи критической точки. Вычисление флуктуационной теплоемкости. Ограничения на применимость теории фазовых переходов Ландау. Новая теория фазовых переходов и понятие о критических индексах. Гипотеза универсальности и соотношения между критическими индексами. Вычисление критических индексов в пространстве 4-ε размерности.
Фазовые переходы второго рода
Удельный термодинамический потенциал остается непрерывным при любых переходах, но его производные могут испытывать разрыв непрерывности. Фазовые превращения, при которых первые производные той же функции остаются непрерывными, а вторые производные меняются скачкообразно, называются фазовыми превращениями второго рода.
Фазовые переходы обнаруживают по изменению свойств и особенностям характеристик вещества в момент фазового перехода. Какая из фаз вещества устойчива при тех или иных условиях, определяется одним из термодинамических потенциалов. При заданной температуре и объеме — это свободная энергия Гельмгольца F(V, T), при заданной температуре и давлении — потенциал Гиббса G(T, р). Потенциал Гельмгольца F — это разность между внутренней энергией вещества Е и его энтропией S, умноженной на абсолютную температуру Т:
(1)И энергия, и энтропия в (1) являются функциями внешних условий (давления p и температуры Т), а фаза, которая реализуется при определенных внешних условиях, обладает наименьшим из всех возможных фаз потенциалом Гиббса. При изменении внешних условий может оказаться, что свободная энергия другой фазы стала меньше. Изменение внешних условий всегда происходит непрерывно, и поэтому его можно описать некоторой зависимостью объема системы от температуры
. Учитывая это согласование в значениях Т и V, можно сказать, что смена стабильности фаз и переход вещества из одной фазы в другую происходят при определенной температуре Т0 на термодинамическом пути 
, а значения 
для обеих фаз являются функциями температуры вблизи этой точки .Вблизи Т0 зависимость
для одной и 
для другой фазы можно приблизить полиномами, зависящими от разности температур 
Разность между свободными энергиями двух фаз принимает вид
Пока разность
достаточно мала, можно ограничиться только первым слагаемым и утверждать, что если 
, то при низких температурах
стабильна фаза I, при высоких температурах — фаза II. В самой точке перехода 
первая производная свободной энергии по температуре испытывает скачок: 
, при 
. По определению, 
— это энтропия вещества. Следовательно, при фазовом переходе энтропия испытывает скачок, определяя теплоту перехода Q, так как 
. Это и есть переходы первого рода.Однако возможно, что совпадут не только свободные энергии, но и их производные по температуре, то есть
. Такая температура не должна быть выделенной; действительно, при 
и в первом приближении по отношению к 
:
и в этой точке фазовый переход не произойдет: тот потенциал Гиббса, который был меньше при В
, будет меньше и при 
. Но иногда существуют причины для того, чтобы при 
одновременно выполнялись 
тогда фаза I становится неустойчивой относительно внутренних степеней свободы при
, а фаза II — при
. В этом случае и происходят переходы второго рода. Название связано с тем, что при переходах второго рода происходит скачок только второй производной потенциала Гиббса по температуре, а вторая производная свободной энергии по температуре определяет теплоемкость вещества.Таким образом, при переходах второго рода должен наблюдаться скачок теплоемкости вещества, но не должно происходить выделение теплоты.
В чем же причины необходимых условий перехода второго рода? Дело в том, что и при
и при существует одно и то же вещество. Взаимодействия между элементами, его составляющими, не изменяются скачком, это и есть физическая природа того, что термодинамические потенциалы для обеих фаз не могут быть независимыми.Уравнения Эренфеста
Фазовые переходы первого рода характеризуются уравнением Клапейрона-Клаузиуса (квазистатические процессы перехода вещества). Согласно уравнению, теплота фазового перехода (например, теплота плавления) определяется выражением:
Между температурой фазового перехода и внешним давлением существует функциональная связь: при фазовом переходе производная (dp / dV) т терпит разрыв. Для фазовых переходов второго рода уравнение Клапейрона- Клаузиуса не применимо, так как из условия равенства первых производных удельного термодинамического потенциала
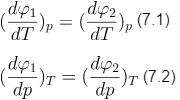
следует равенство удельных энтропий и объемов:
Это приводит к тому, что в правой части уравнения одновременно обращаются в нуль числитель и знаменатель, и в уравнении Клапейрона- Клаузиуса возникает неопределенность вида 0/0.
Найдем полные дифференциалы удельных энтропий и объемов, и в соответствии с формулами (7.1) и (7.2) приравняем их
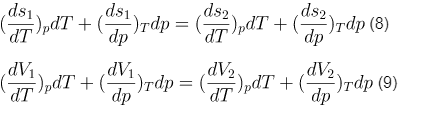
Проведем преобразование полученных выражений. Производная удельной энтропии по температуре в обратимом процессе может быть представлена в виде
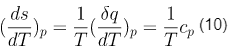
где q — удельная теплота, ср — удельная изобарическая теплоемкость.
Так как для второй производной удельного термодинамического потенциала может быть записано равенство:
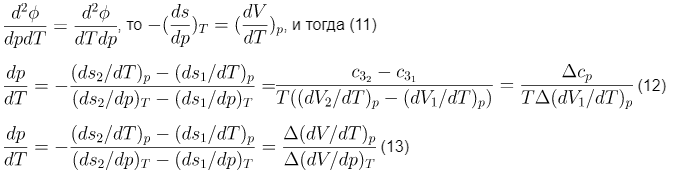.Полученные выражения позволяют записать уравнения, связывающие производную давления от температуры
(наклон кривой равновесия) со скачками удельной изобарической теплоемкости cp и величин 
, связанных с температурным коэффициентом объемного расширения и коэффициентом изотермической сжимаемости:
.Эти уравнения называются уравнениями Эренфеста, и они имеют вид
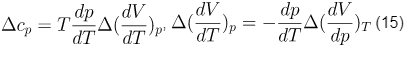
Флуктуации вблизи точки фазового перехода II рода. Теория ОрнштейнаЦернике.
Вблизи точки перехода в связи с резким изменением параметра порядка следует ожидать аномального возрастания флуктуаций η. В первую очередь это связано с обращением в бесконечность восприимчивости в точке перехода. Действительно, при фиксированных температуре и давлении вероятность флуктуации w имеет вид:
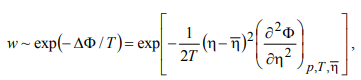(16)Следовательно, средний квадрат флуктуаций
(17)Вблизи точки перехода зависящие от параметра порядка члены разложения термодинамического потенциала Ф(p,T,η)представляют собой малую добавку к независящей от параметра порядка части
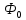(p,T ). Поэтому согласно теореме о малых добавках можно написать аналогичное разложение для Ω(µ,T,η):