ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(18)Разложение (18) относится к однородной среде. В неоднородной среде должна быть учтена зависимость от производных параметра порядка. При этом Ω−потенциал запишется в виде интеграла по объему от некоторой функции. Члены первого порядка по первым производным параметра порядка вида f(η)∇η отсутствуют, так как при интегрировании по объему преобразуются в интегралы по поверхности, представляющие собой не интересующий нас поверхностный эффект. Первые члены, которые должны быть учтены, это члены пропорциональные
. Однако при интегрировании по объему такие члены сводится друг к другу интегрированием по частям. В итоге флуктуационная часть Ω-потенциала представляется в виде разложения по степеням действительного, скалярного параметра порядка η(r):
(19)Коэффициенты α, b являются положительными функциями температуры, вычисленными при T=Tc, а отношение
имеет размерность квадрата длины, пропорциональной радиусу действия потенциала R0, приводящего к возникновению параметра порядка. Вариация функционала (19) приводит к уравнению:
(20)Можно заметить, что для малых значений параметра порядка, когда можно пренебречь нелинейным слагаемым, уравнение для Ω-потенциала имеет вид произведения суммы операторов типа кинетической и потенциальной энергии на флуктуирующий параметр порядка (в отсутствии поля):
(21)Согласно теореме о малых добавках аналогичное выражение можно написать и для энергии:
(22)При малых значениях параметра порядка можно пренебречь в (22) нелинейным членом. При этом выражение для энергии заменяется на следующее:
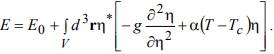
(23)
Поэтому энергию можно рассчитывать следующим образом:
(24)где уровни энергии рассчитываются согласно уравнению типа Шредингера c оператором кинетической энергии − g
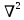и оператором потенциальной энергии α(T –Tc):
(25) а 
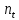- числа заполнения состояний.Энергию колебаний, Et, которую находим из уравнения (25), называют энергией критических колебаний. В результате подстановки η=exp(iqr) получаем простой закон дисперсии:
(26)C учeтом того обстоятельства, что наибольший вклад дает область малых
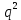, когда T→Tc, cингулярную часть энтропии находим с помощью дифференцирования температурно-зависящей части энергии критических колебаний. Таким же способом вычисляем сингулярную часть теплоемкости:
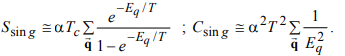(27)После перехода к интегрированию в сферической системе координат дело сводится к вычислению простого интеграла:
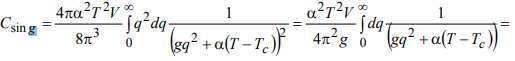
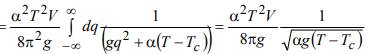(28)Этот результат необходимо сравнить со скачком теплоемкости в теории Ландау ∆
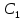=VTc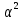
/2b. В результате получаем условие применимости метода самосогласованного поля:
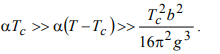(29)]Для сверхпроводника это условие дает весьма широкую область применимости, в основном по причине малости коэффициента b.
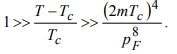(30)В случае гейзенберговского ферромагнетика параметры α,g,b,Tc, имеют значения:
(31)
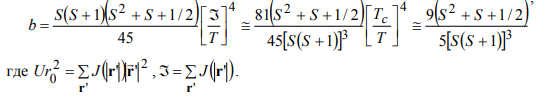(32)В этом случае, учитывая, что U и ℑ одного порядка, условие применимости существенно зависит от величины
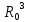, обезразмеренной на объем элементарной ячейки 
: 
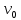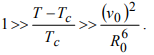(33)Таким образом, если радиус действия потенциала совпадает с размером элементарной ячейки, тогда область применимости метода самосогласованного поля отсутствует, а вместо скачка теплоемкости наблюдается сингулярный рост.
Теория Ландау
Из приведенных вычислений видно, что при приближенных подсчетах потенциала Гиббса для модели Изинга на промежуточных этапах возникает потенциал, минимумы которого соответствуют потенциалам Гиббса разных фаз. Эта функция — потенциал Ландау — должна существовать всегда, когда структуры фаз близки между собой. Его можно ввести в рассмотрение, если в перестройке структуры при переходе из одной фазы в другую участвует ограниченное число степеней свободы кристалла (в описанном примере модели Изинга параметром порядка является плотность ферромагнитного момента кристалла).
Теория Ландау основана на представлении о связи фазового перехода второго рода с изменением группы симметрии физической системы. Л. Д. Ландау предположил, что свободная энергия любой системы должна удовлетворять двум условиям: быть аналитической функцией и соблюдать симметрии гамильтониана. Тогда (в окрестности критической температуры T0) термодинамический потенциал Гиббса можно разложить по степеням параметра порядка:
(34)где а, в — коэффициенты разложения,п—параметр порядка,
h— напряженность поля. С учетом модели Изинга, свободная энергия может быть записана следующим образом:
(35)В этой теории Ландау впервые применил понятие параметра порядка — термодинамическую величину, характеризующую дальний порядок в среде, возникающий в результате спонтанного нарушения симметрии.
Итак, в точке перехода появляется параметр порядка, равный нулю в менее упорядоченной фазе и изменяющегося от нуля до ненулевых значений в более упорядоченной фазе. Вследствие чего изменение симметрии тела при фазовом переходе второго рода обладает следующим общим свойством: симметрия одной из фаз является более высокой по отношению к другой фазе (тогда как при фазовом переходе первого рода изменение симметрии тела не подчинено никаким ограничениям). В большинстве случаев более симметричная фаза соответствует более высоким температурам, а менее симметричная — более низким. В частности, переход второго рода из упорядоченного в неупорядоченное состояние происходит всегда при повышении температуры (исключение — точка Кюри сегнетовой соли, ниже которой кристалл относится к ромбической, а выше — к моноклинной системе).
С существованием неравновесного потенциала Ландау связаны некоторые свойства фазовых переходов второго рода. Например, при переходах второго рода не имеет место правило фаз Гиббса: в одной точке на фазовой р-Т диаграмме не может сосуществовать более трех фаз одного вещества. При выводе правила фаз существенно используется предположение о независимости их потенциалов Гиббса. При переходах второго рода потенциалы граничащих фаз не независимы. Поэтому сосуществование более трех фаз невозможно, а граничить в одной точке перехода второго рода могут и более трех фаз.
Некоторые примеры фазовых переходов второго рода
Наиболее иллюстративным примером фазового перехода второго рода является превращение жидкого Не I в жидкий Не II при температуре 2,2 К и ниже. С этим фазовым переходом связано квантовое явление сверхтекучести, возникающее в Не II. Это явление было открытое в 1938 г. П. Л. Капицей и теоретически объяснено советским физиком-теоретиком Л. Д. Ландау.
Теория сверхтекучести основывается на предложении о том, что Не II представляет собой смесь двух жидкостей, хотя с точки зрения квантовой физики атомы Не II нельзя разделить на два различных вида. Однако классическая аналогия наиболее удобна для восприятия и согласно ей одна компонента Не II является сверхтекучей, а другая — нормальной (не сверхтекучей). Таким образом течение Не II можно представить в виде потоков двух жидкостей, при этом вязкость сверхтекучей компоненты равна нулю.
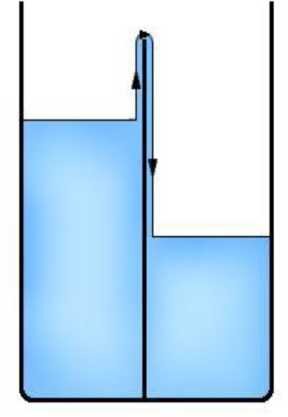
Рисунок 1. Образование ползущей пленки в сосудах с Не II
Именно в отсутствии вязкости у Не II и состоит явление сверхтекучести. Отсутствие вязкости приводит к тому, что Не II может проникать через очень узкие капилляры (П.Л. Капица ставил опыты по протеканию Не II между двумя шлифованными стеклами), а также к тому, что уровни Не II, налитого в два разделенных перегородкой сосуда, постепенно выравниваются из-за образования ползущей пленки (см. рис. 1).
Ползущая пленка имеет толщину менее 10" м. При ее движении со скоростью несколько десятков сантиметров в секунду жидкость перетекает из одного сосуда в другой.
Нормальная компонента переносит при своем движении теплоту, а сверхтекучая компонента — нет. При протекании Не II через узкую щель, перетекает главным образом сверхтекучая часть Не II. Поэтому вытекающий Не II должен иметь более низкую температуру, чем Не II в сосуде из которого происходит вытекание. Это явление было использовано для получения сверхнизких температур, составляющих десятые доли кельвина.
К фазовым переходам второго рода относятся также переход некоторых веществ в сверхпроводящее состояние при низких температурах. Такой переход сопровождается падением до нуля электрического сопротивления сверхпроводников. Примером фазового перехода второго рода является переход железа из ферромагнитного в парамагнитное состояние в точке Кюри. К ним относятся также переходы, связанные с изменением симметрии кристаллической решетки, в тех случаях, когда тип симметрии решетки при переходе становится другим (например, переход от кубической к тетрагональной решетке).
При фазовом переходе второго рода все свойства вещества изменяются непрерывным образом во всем объеме вещества. Поэтому при их протекании невозможно существование метастабильных состояний, характерных для фазовых переходов первого рода.
Вывод
Представление о переходах второго рода имеет обширное практическое значение: во многих случаях оно оказывается продуктивным при предсказании свойств одних фаз вещества по характеристикам других его фаз.
В начале работы было замечено, что существует два вида фазовых переходов. Но стоит упомянуть, что современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода. В последнее время, например, широкое распространение получило понятие квантовый фазовый переход, т.е. фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур, где классический фазовый переход не может реализоваться вследствие теоремы Нернста.