Файл: Контрольная работа По дисциплине Информационные технологии в корпоративных сетях.docx

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

Контрольная работа

По дисциплине «Информационные технологии в корпоративных сетях»

Санкт-Петербург

2023

Оглавление

Задание.

Разработка тестов для проверки степени усвоения уч. материала

Этапы выполнения задания

1. Ознакомиться с полученным текстом.

2. Разбить материал на «уроки», имеющие законченный смысл. «Уроки» должны быть не слишком маленькими, чтобы было возможным сформулировать по каждому уроку один или несколько тестовых вопросов.

3. По всем выделенным «урокам» сформулировать тестовые вопросы.

4. К каждому тестовому вопросу предложить несколько ответов, один или несколько из них должен быть правильным, а остальные - неверными.

5. Озаглавить либо оцифровать каждый урок и его разделы, если вопросы относятся к каким-либо фрагментам урока.

6. К каждому неверному ответу дать ссылку на тот фрагмент, по которому был сформулирован тестовый вопрос.

7. Оформить отчет. В отчете привести исходный текст, его структуру (см.п.5) и тесты с ответами и ссылками к каждому уроку

Контрольная работа выполняется без применения каких-либо программных средств, должна быть оформлена в Word (любой версии) и должна содержать:

- титульный лист;

- номер варианта, в скобках указать номер студенческого билета;

- исходный текст

- краткое изложение теоретической части; сформированные тесты

- заключение.

По учебнику (Гламаздин, Е. С. Управление корпоративными программами)

Вариант 21. ч.2 параграф 2.4 Модели и методы оптимизации структуры управляющей компании

Исходный текст

2.4. Модели и методы оптимизации структуры управляющей компании

В первом разделе решены задачи согласования интересов элементов

---

системы управления корпоративными программами, а также задача выбора управляющей компании. Во втором разделе – задачи планирования (выбора вариантов реализации корпоративных проектов), в третьем – задачи оперативного управления процессом реализации корпоративных проектов и программ. В настоящем разделе рассматриваются две модели формирования и оптимизации структуры управляющей компании. Первая модель основывается на решении задач «назначения» – определения распределения активных элементов по работам проектов, вторая – на результатах исследования активных систем с распределенным контролем, приведенных в первом разделе и в [23, 25, 43, 46].

Для большинства современных организаций и фирм (не только для компаний, управляющих реализацией корпоративных программ) актуальна проблема поиска рационального баланса между функциональной и проектной структурой. Линейная структура, порождаемая функциональной¹ специализацией, оказывается эффективной при процессном функционировании, то есть в условиях относительного постоянства набора реализуемых системой функций. При проектной структуре участники системы «привязаны» не к функциям, а к проектам, которые могут сменять друг друга во времени (см. подробное обсуждение свойств линейных, матричных и сетевых структур в [19, 40]). Гибридом функциональной и проектной структур является матричная структура, в которой каждый исполнитель в общем случае подчинен одновременно нескольким руководителям – например, некоторому функциональному руководителю и руководителю определенного проекта.

Поэтому ниже рассматриваются модели, учитывающие плюсы и минусы различных структур и позволяющие определять оптимальные (по оговариваемому в каждом конкретном случае критерию) типы структур.

Отметим, что речь идет именно о типе структуры, так как задача синтеза оптимальной иерархической структуры в целом не рассматривается (см. соответствующие модели в [19, 28, 38, 40, 59]) – исследование ограничивается анализом простейших двухуровневых «блоков».

Модель «назначения». Пусть в системе имеются n АЭ – исполнителей работ по корпоративным проектам (I = {1, 2, …, n} – множество АЭ) и m ≤ n центров, каждому из которых поставлен в соответствие некоторый тип работ. Тогда проект (выбираемый за единицу времени) может характеризоваться вектором v = (v

---

₁, v₂, …, v_m) объемов работ, где v_j≥ 0, j Є M – множеству работ (центров).

Введем матрицу 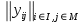, элемент y_ij≥ 0 которой отражает объем работ j-го типа, выполняемый i-ым АЭ. Обозначим 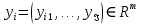– вектор объемов работ, выполняемых i-ым АЭ, 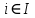, 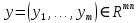– вектор распределения работ по АЭ.

Если 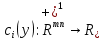– функция затрат i-го АЭ, то задача распределения работ может быть сформулирована в виде:

(1)



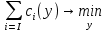
(2)



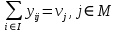
Отметим, что в задаче (1)-(2) не учитываются ограничения на объемы работ, выполняемые АЭ.

Если функции затрат выпуклые по соответствующим переменным, то (1)-(2) – задача выпуклого программирования. Оптимальное значение целевой функции (1) обозначим C₀(v).

Например, если



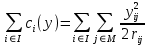
то 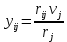, где



Содержательно задача (1)-(2) соответствует определению структуры взаимосвязей между АЭ и центрами (напомним, что каждый центр «отвечает» за некоторую работу). В общем случае каждый АЭ оказывается связан с каждым центром, так как первый выполняет в оптимальном распределении работ работы нескольких (быть может, даже всех) типов. Можно условно считать, что подобным связям соответствует матричная структура управления (описываемая матрицей 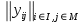, являющейся решением задачи (1)-(2) и называемой иногда матрицей ответственности), эффективность которой зависит от рассматриваемого проекта v и равна C₀(v). Поэтому задачу (1)-(2) можно условно назвать задачей синтеза оптимальной матричной структуры.

Альтернативой является использование функциональной структуры, в которой каждый АЭ закреплен за одним и только одним центром (типом работ). Для того, чтобы найти оптимальную функциональную структуру, следует решить задачу назначения исполнителей. Сформулируем эту задачу.

---

Пусть функции затрат АЭ сепарабельны:

(3)



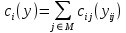
Тогда задача поиска оптимальной функциональной структуры заключается в нахождении такого разбиения S множества АЭ I на m непустых подмножеств 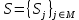(между элементами которых работа соответствующего типа распределяется по аналогии с задачей (1)-(2)), что суммарные затраты по выполнению всего объема работ в рассматриваемом проекте минимальны.

Задача распределения объемов j-ой работы между элементами множества 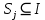имеет вид:

(4)



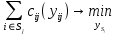
(5)



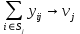
Где 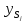– вектор действий АЭ из множества .

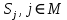Обозначим C_j(S_j , v_j) – оптимальное значение целевой функции (4). Тогда задача синтеза функциональной структуры заключается в нахождении разбиения S минимизирующего сумму затрат, полученных из решения задач (4)-(5) для всех :

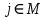(6)



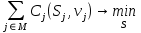
Обозначим C(v) – оптимальное значение целевой функции в задаче (6).

Утверждение 10. .

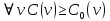Доказательство утверждения 10. При сепарабельных функциях затрат АЭ



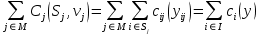
То есть целевые функции (1) и (6) (с учетом (4)) в задачах синтеза оптимальной матричной и функциональной структур совпадают. В последней задаче допустимое множество не шире, следовательно, и значение целевой функции не меньше. Утверждение 10 доказано.

Эффективности C(v) и C₀(v), соответственно, функциональной и матричной структур являются косвенными оценками максимальных дополнительных затрат на управление, возникающих при переходе от линейной (функциональной) к матричной структуре управления. Поясним последнее утверждение. Функциональная структура, как известно [19, 40, 47, 48], требует минимальных затрат на управление (собственное функционирование). Но, она приводит к неэффективному распределению работ между АЭ – см. утверждение 10. С другой стороны, матричная структура приводит к более эффективному распределению работ, но требует больших затрат на управление. Поэтому при решении вопроса о выборе структуры (или переходе от одной структуры к другой) следует принимать во внимание оба фактора: затраты на управление и эффективность распределения работ (эффективность структуры). Если последняя может быть оценена количественно (см. задачи (1)-(2) и (4)-(6)), то определение затрат на управление является сложной задачей, решаемой на практике, зачастую, интуитивно. Исходя из этого, можно сказать, что если затраты на управление при использовании матричной структуры превышают затраты на управление при использовании линейной структуры не более, чем на

---

C(v) – C₀(v), то предпочтительно использование матричной структуры, в противном случае – линейной.

Кроме того, во многих реальных организациях одна подструктура является матричной, а другая – линейной. Определение рационального баланса (между ними двумя одновременно) может производиться по аналогии с формулировкой и решением задачи (4)-(6).

Если задача (4)-(5) является стандартной задачей математического программирования, то задача (6) принадлежит к задачам дискретной оптимизации. Решение ее в случае больших значений m и n может оказаться чрезвычайно трудоемким. Поэтому для того, чтобы сделать хоть какие-то качественные выводы, введем ряд упрощающих предположений.

Рассмотрим частный случай, когда число АЭ равно числу работ, затраты АЭ сепарабельны и удельные затраты c_ij i-го АЭ по выполнению j-ой работы постоянны, .

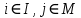Тогда элементы разбиения S – одноэлементные множества и задача (1)-(2) принимает вид:

(7)



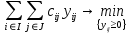
(8)



а задача (4)-(6) превращается в следующую стандартную задачу о назначении:

(9)



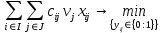
(10)



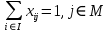
(11)



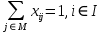
В силу линейности целевой функции (7), решение задачи (7)- (8) тривиально: 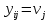, есл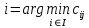и , и 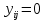, если 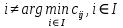, то есть следует поручать весь объем работ j-го типа поручать тому АЭ, который выполняет его с наименьшими удельными затратами. При этом может оказаться, что все работы выполняет один АЭ. Это распределение работ будет оптимально по критерию суммарных затрат, но может быть нереализуемым на практике.

Для того чтобы уйти от тривиального (и иногда нереализуемого) решения, введем ограничения Y_i на максимальный суммарный объем работ, которые может выполнять i-ый АЭ, .

С этими ограничениями задача (7)-(8) превращается в следующую стандартную транспортную задачу:

---