СОДЕРЖАНИЕ

ВВЕДЕНИЕ 2

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ 4

АСИМПТОТИКА РЕШЕНИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА ПРИ ВЕЩЕСТВЕННЫХ X. ГЛАВНЫЙ ЧЛЕН АСИМПТОТИКИ 9

ЗАКЛЮЧЕНИЕ 12

СПИСОК ЛИТЕРАТУРЫ 13
ВВЕДЕНИЕ
Большинство физических проблем, с которыми сегодня сталкиваются инженеры, физики и эксперты в области прикладной математики, обнаруживают множество важных особенностей, которые не позволяют им получать точные аналитические решения. Такими особенностями являются, например, нелинейность, переменные коэффициенты, границы сложной формы и нелинейные граничные условия на известных или в некоторых случаях неизвестных границах. Даже если точное решение какой-либо проблемы явно найдено, оно может оказаться бесполезным для математической и физической интерпретации или численных расчетов. Примерами таких задач являются большие функции Бесселя и двоичные периодические функции для больших значений аргументов. Поэтому мы вынуждены прибегать к приближениям, численным решениям или комбинации этих 2-х методов, чтобы получить информацию о решении уравнения. Среди методов аппроксимации в первую очередь необходимо упомянуть метод асимптотических возмущений, который является предметом данного исследования. Согласно этим методам, решение представлено некоторым 1 членом асимптотического разложения, число которых обычно не превышает 2. Разложение может осуществляться по большим или малым параметрам, которые естественным образом встречаются в уравнении или вводятся искусственно для удобства. Такое расширение называется возмущением параметра. С другой стороны, разложение может быть выполнено по координатам больших или малых значений, и в этом случае они называются координатными возмущениями. Глава 1 содержит обозначения, определения и действия для асимптотического разложения. Примеры декомпозиции по параметрам и координатам и их существенные свойства описаны в пунктах. To формализовать концепцию пределов, оценки ошибок, определения символов порядка и другие спецификации представлены в разделе 1.3. Раздел 1.4 содержит определение асимптотического разложения, асимптотической последовательности и степенного ряда, а также Раздел 1.5 содержит сравнение между сходящимся рядом и асимптотическим рядом. Далее в разделе определяются равномерные и неоднородные асимптотические разложения. Краткое описание операции по асимптотическому разложению приведено в разделе. В главе 2 описывается, как изучать асимптотическое поведение решений обыкновенных линейных дифференциальных уравнений. Идея этого метода заключается в преобразовании заданной системы дифференциальных уравнений в специальную форму, называемую L - диагональной. В некоторых случаях такого рода преобразование может быть выполнено путем элементарной линейной подстановки. Построение асимптотического разложения после преобразования решения линейного дифференциального уравнения в L-диагональную форму очень просто. Полезно сделать несколько общих замечаний о характеристиках рассматриваемой функции. Все числовые функции и параметры, о важности которых не делается никаких особых оговорок, в общем случае следует считать сложными. Например, в начале главы 2 предполагается, что коэффициенты и искомые функции дифференциального уравнения являются комплексными значениями в общем случае, когда t является действительным (с полубесконечным интервалом, определенным для t). Определите абсолютную непрерывность этой функции в соответствующем замкнутом интервале, определив суммируемость производных функции в определенном интервале. Везде, где рассматривается система дифференциальных уравнений с суммируемыми коэффициентами, ее решение

---

подразумевает набор абсолютно непрерывных функций, которые удовлетворяют уравнению практически в любом месте заданного интервала.

ГЛАВА 1 – ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ
Уравнение вида:



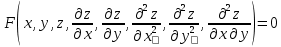
Есть дифференциальное уравнение 2-го порядка с 2 переменными x и желаемой функцией z от y. Уравнения математической физики линейны, в отличие от уравнений с общей формой частных производных порядка 2, т.е. они линейно зависят от искомой функции и ее частных производных. Например, для 2 независимых переменных они имеют вид:



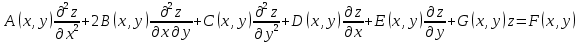
Уравнение называется однородным, если 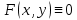, если 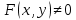, то уравнение называется неоднородным.

Обозначаем левую часть уравнения через 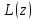, тогда можно записать в виде:

.

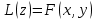Соответствующее однородное уравнение примет вид:

.

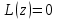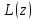- линейный дифференциальный оператор. Самостоятельно проверить свойства линейности оператора .

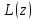Следующее утверждение непосредственно следует свойству линейности оператора L(z):

Теорема 1.1. Если Z (x,y) является решением линейного однородного уравнения, то функция Cz (x,y) также является решением уравнения, а C - любая постоянная.

Теорема 1.2. Если Z_1 (x,y) и z_2 (x,y) являются решениями линейных однородных уравнений, то сумма z_1 (x,y) + z_2 (x,y) также является решением этого уравнения.

Следствие. Линейная комбинация с произвольными постоянными коэффициентами k решений уравнения 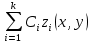также является решением этого уравнения.

В отличие от обычных линейных однородных дифференциальных уравнений с конечным числом линейно независимых частных решений, линейная

---

комбинация дает общее решение этого уравнения, но уравнение в частных производных может иметь бесконечный набор линейно независимых частных решений.

Например уравнение:



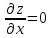
имеет общее решение 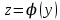, поэтому его решениями будут, например, функции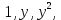

Для линейного неоднородного:

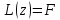- уравнения справедливы.

Теорема 1.3. Если 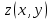- решение линейного неоднородного уравнения, а 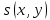- решение соответствующего однородного уравнения, сумма 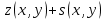также является решением неоднородного уравнения.

Теорема 1.4. Если 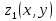- решение уравнения 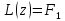, а 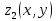- решения уравнения 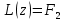, то сумма 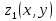+ 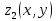является решением уравнения .

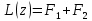Рассмотрим классификацию дифференциальных уравнений 2-го порядка с 2 независимыми переменными. Определение. Линейное дифференциальное уравнение второго порядка в некоторой области 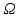на плоскости хОу называется:

гиперболическим в 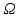, если 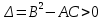в ;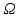

эллиптическим в 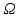, если 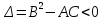в ;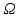

параболическим в

---

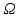
, если 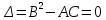в .

Простейшим из гиперболических уравнений является волновое уравнение:

.

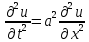Это обнаруживается в проблемах, связанных с процессом вибрации. Простейшим из уравнений эллиптического типа является уравнение Лапласа

.

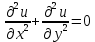Интеграл этого уравнения достигается при изучении стационарных процессов.

Простейшим уравнением параболического типа является уравнение теплопроводности (уравнение Фурье):

.

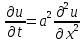Это часто встречается при изучении теплопроводности и диффузионных процессов. Позже мы рассмотрим эти уравнения более подробно.

В курсе математической физики также изучаются более общие формы волновых уравнений, уравнений Лапласа и уравнений Фурье:

, ,

,

, .

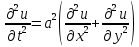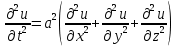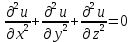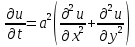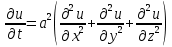Уравнение приводится к каноническому виду в достаточно малой окрестности любой заданной точки. Предположим, что коэффициенты A, B и C уравнения принадлежат классу C ^ 2 в некоторой окрестности и в то же время нигде в нем не исчезают. Чтобы быть уверенным, мы можем предположить≠0 в этой окрестности. Конечно, в противном случае вы могли бы найти C≤0, но если вы поменяете местами x и y, то получите уравнение с a≤0.Если A и C равняются нулю в какой-то точке одновременно, то B ≤0 вблизи этой точки.В этом случае после деления на 2 уравнение уже будет иметь канонический вид:

.

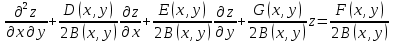Теперь давайте перейдем к новой переменной:

, , ,

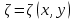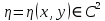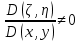Тогда:

---

,

,

,

, .

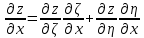
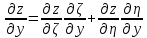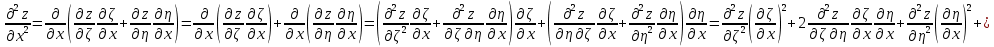
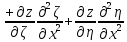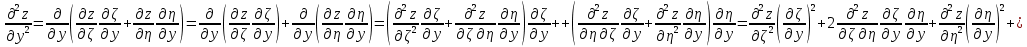
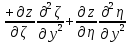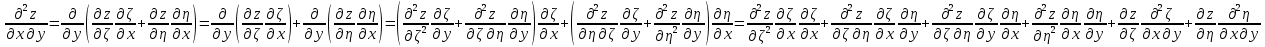Поэтому уравнение примет вид:

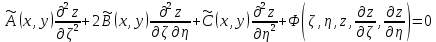, где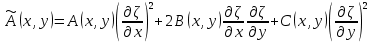

,

,

.

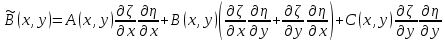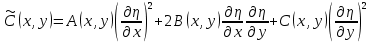Потребуем, чтобы функции и 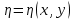обращали в нуль коэффициенты 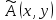и 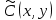, т.е. удовлетворяли уравнениям:

,

.

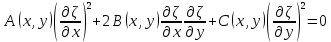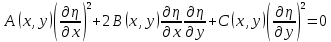Так как 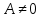, то эти уравнения эквивалентны линейным уравнениям

, ,

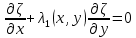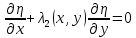где , , .

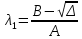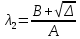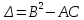Как мы с вами заметили, в зависимости от 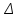возможны три типа уравнений. Рассмотрим отдельно эти три случая.

Гиперболический тип, .

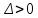В этом случае уравнение приводится к каноническому виду:



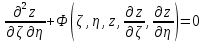
Замена переменных 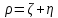, 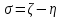приводит уравнение к другому, эквивалентному, каноническому виду:

---

Смотрите также файлы

• 1. основы маркетинга лекция методологические основы дисциплины МАркетинг. Часть 1.pdf

• Информационный лист для учебного занятия, реализуемого с применением дистанционных образовательных технологий и электронного обучения.doc

• Пример задания 1.doc

• Дисциплина Безопасность жизнедеятельности Раздел Теоретические основы безопасности жизнедеятельности Тема Объект, предмет, методология, теория и практика безопасности.doc

• Задание Решите ситуационную задачу, используя предложенную методику.docx