Пример задания №1

Задание 1.1

Проверить гипотезу о подчинении равномерному закону десяти чисел двух левых столбцов таблицы 1.1 по критерию согласия (КС) Колмогорова.

Таблица 1.1

80	25	12	29	89	84	98	46	42	62
69	43	75	41	47	16	18	80	16	38
41	86	60	75	29	85	48	71	06	68
80	67	93	63	39	75	53	71	35	88
24	48	13	86	53	95	24	77	37	61

Запишем случайные числа по возрастанию: 24, 25, 41, 43, 48, 67, 69, 80, 80, 86.

Построим эмпирическую функцию распределения.

F^*(x) F(x)
1,0




0,8

---

0,6



0,4 max разница возможна при х=48,

при х=25, при х=86.

0,2






x

20 40 60 80 100

Рис.1.1

Вычислим основные статистические характеристики распределения случайных чисел.

1. 
   Оценка первого начального момента вычисляется по формуле:
   

=(24+25+41+43+48+67+69+80+80+86)/10=56,3.

Оценка второго начального момента вычисляется по формуле:

=(24²+25²+· · · +86²)/10=3648,1.

Оценка среднего квадратического отклонения (стандартного отклонения) вычисляется по формуле:

---

= =21,873.

=56,3–1,732·21,873=18,416.

=56,3+1,732·21,873=94,184.

По двум точкам с координатами (18,4;0) и (94,2;1) на рис.1 построим прямую, являющуюся гипотетической функцией распределения. Ввиду некоторой неточности рис.1.1 точно определить максимальную разницу между эмпирической и гипотетической функциями распределения не представляется возможным. Поэтому вычислим значения гипотетической функции распределения для всех аргументов по формуле:


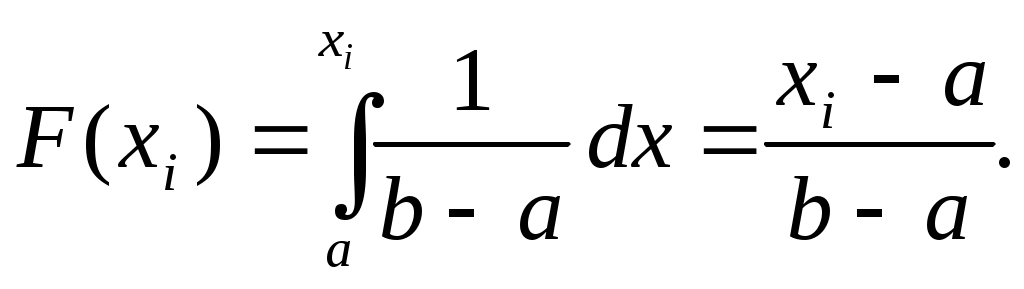
Результаты вычислений представим в таблице 1.2.

Таблица 1. 2

i	xi	F*(xi)	F(xi)	F*(xi)- F(xi)
1	24	0,1	0,074	0,026
2	25	0,2	0,087	0,113
3	41	0,3	0,298	0,002
4	43	0,4	0,324	0,076
5	48	0,5	0,390	0,110
6	67	0,6	0,641	- 0,041
7	69	0,7	0,668	0,032
8	80	0,8	0,813	- 0,013
9	80	0,9	0,813	0,087
10	86	1,0	0,892	0,108

По результатам таблицы 2 определяем

---

максимальную разницу в функциях распределения, равную 0,113, и вычислим КС Колмогорова.


По статистической таблице 1.3 находим коэффициент доверия высказанной гипотезе р_к=0,9985 и так как он превышает рекомендуемое значение 0,2, то делаем заключение что. имеющиеся статистические данные не противоречат гипотезе об их подчинении равномерному закону по КС Колмогорова. В таблице 1.3 жирным цветом выделены значения К, при которых гипотеза о подчинении исходных случайных чисел равномерному закону не отвергается.
Таблица 1.3

рк	1.0000	1.0000	1.0000	1.0000	0.9970	0.9640	0.8640
К	0.0000	0.1000	0.2000	0.3000	0.4000	0.5000	0.6000
рк	0.7110	0.5440	0.3930	0.2700	0.2000	0.1120	0.0680
К	0.7000	0.8000	0.9000	1.0000	1.0500	1.2000	1.3000
рк	0.0400	0.0220	0.0121	0.0060	0.0030	0.0020	0.0010
К	1.4000	1.5000	1.6000	1.7000	1.8000	1.9000	2.0000

Задание 1.2

Проверить гипотезу о подчинении равномерному закону ста одноразрядных чисел всех столбцов таблицы 1.1 по критерию согласия

---

χ².

Подсчитаем количество символов каждого типа и построим гистограмму, представленную на рис.2.1.

М_i^*

16




12 М_i=10




8




4

5 10 8 10 11 9 13 10 16 8

---

Смотрите также файлы

• Дисциплина Безопасность жизнедеятельности Раздел Теоретические основы безопасности жизнедеятельности Тема Объект, предмет, методология, теория и практика безопасности.doc

• Задание Решите ситуационную задачу, используя предложенную методику.docx

• Тесты для воспитателей и родителей Подобрать и апробировать формы и содержание работы по привлечению родителей к деятельности доу.docx

• Самозащита гражданских прав и меры оперативного воздействия как способы защиты гражданских прав.docx

• Котлекарь кот может безошибочно определить, где у хозяина больное место. Он ложится прямо на больной сустав и начинает его лечить. И ведь действительно помогает. Объясните, что за странное чутье и лекарские способности у котов Ответ.docx