Чтобы доказать это представление, мы покажем, что существует по крайней мере одна пара решений уравнений π и n, удовлетворяющих условию. Во-первых, давайте установим взаимосвязь между этими решениями и характеристиками уравнения. Предположим, что существуют решения уравнений, такие что 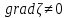, 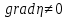в рассматриваемой окрестности, тогда кривые:

,

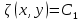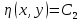
Определите 2 семейства характеристик уравнения. Давайте теперь докажем следующее вспомогательное утверждение.

Лемма. Пусть функция 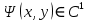такая, что 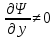. Для того, чтобы семейство кривых 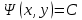определяло характеристики уравнения, необходимо и достаточно, чтобы выражение 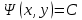было общим интегралом одного из обыкновенных дифференциальных уравнений

,

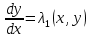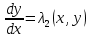
Это уравнение называется дифференциальным уравнением характеристики уравнения.

ГЛАВА 2 – АСИМПТОТИКА РЕШЕНИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА ПРИ ВЕЩЕСТВЕННЫХ X. ГЛАВНЫЙ ЧЛЕН АСИМПТОТИКИ
В предыдущем разделе было определено понятие асимптотической декомпозиции и представления явно заданных функций. Как правило, задача приложения сложнее, чем нахождение асимптоты заданной функции. Физическая величина как функция переменной определяется неявно с помощью различных уравнений (дифференцирование, интегрирование и т.д.). Однако не всегда возможно получить асимптотическое значение искомой функции в 2 этапа. Сначала найдите функцию явно, затем найдите ее декомпозицию. В этом случае первый шаг опускается, и асимптотическое значение определяется непосредственно из уравнения.

Многие проблемы, возникающие в теоретической физике, приводят к дифференциальным уравнениям второго порядка с переменными коэффициентами. В этом разделе мы рассмотрим методы аппроксимации для решения уравнений вид аy′′ + p(x)y′ + q(x)y = 0, при

---

x→ ∞.
2.1 Главный член асимптоматики
Решения можно сравнить с решением некоторого эталонного уравнения. Если положить, например, p(x) = 0,

q(x) = ±1, то уравнение примет вид

y^′′ ± y= 0.

Как известно, для него существуют, соответственно знаку пе ред y, по паре линейно независимых решений e^±ixи e^±x.

Зададимся вопросом: при каких условиях уравнения

y^′′ ± q(x)y= 0

имеют решения, эквивалентные на бесконечности функциям

e^±ixили e^±x? Ответ даст ряд теорем.

Положим функцию q(x) в уравнении (10) равной q(x) = 1 + ϕ(x).
2.2 Лимма 1.
Если функция ϕ(x) удовлетворяет условиям:

lim

x→∞

ϕ(x) = 0,

2.^∫∞ |ϕ(x)|dx<∞,

тоуравнение:

y^′′ + (1 + ϕ(x))y= 0

обладает двумя решениями, имеющие соответственно асимптотическийвидприx→ ∞:

y_1,2 = e^±ix+ o(1)

иливвещественнойформе:

y₁ = sin x+ o(1),y₂ = cos x+ o(1).

2.3 Лимма 2.
Если функция ϕ(x) удовлетворяет условиям:

limx→∞

ϕ(x) = 0,

2.^∫

---

∞ |ϕ(x)|dx<∞,

то уравнение

y^′′ − (1 + ϕ(x))y= 0

обладает двумя решениями, имеющие соответственно асимптотическийвидприx→∞:

y_3,4 = e^±x+ o(1) .
Теоремы A и B говорят о форме первого члена асимптотического представления решения уравнения. Этот член называется основным асимптотическим решением уравнения. Дополнительные предположения о функциях сделаны ниже ϕ(x), что позволит уточнить асимптотики y_1,2 и y_3,4, то есть получить следующий наименьший член в асимптотическом представлении и тем самым уменьшить ошибку в приближении.

Процесс нахождения асимптотического разложения решения уравнения можно разделить на 2 этапа. Сначала постройте последовательность калибровки {ψ_k(x)} так называемые формальные асимптотические решения:

∞

y=c_kψ_k(x).

k=1

Частичная сумма

n

y_n=c_kψ_k(x)

k=1

ряда (13) должна удовлетворять условию:


y^′′ ± q(x)y^ = o(ψ(x)),x→ ∞_nn
для любого n. В^о вторых, доказать, что существует решение y(x) уравнения (10), которое разлагается в построенный выше формальный ряд. Это означает, что для любого nвыполняется условие:


^
y(x) − y_n(x) = O(ψ_n+1(x)),x→ ∞.

Ещё раз отметим, что асимптотический ряд (13) не обязан сходиться.

ЗАКЛЮЧЕНИЕ
Обсуждается один из методов изучения асимптотического поведения решения линейных дифференциальных уравнений. Идея этого метода заключается в преобразовании заданной системы дифференциальных уравнений в специальную форму, называемую L-диагональной. В некоторых случаях такого рода преобразование может быть выполнено путем элементарной линейной подстановки. Построение асимптотического разложения после преобразования решения линейного дифференциального уравнения в L-диагональную форму очень просто. Мы также предоставляем общую информацию об асимптотическом разложении и решаем задачу нахождения оптимального алгоритма для нахождения асимптотических методов для системы дифференциальных уравнений второго порядка.

---

Как мы видим, предложенный метод хорошо реализован для определенных задач. Главное преимущество этого метода заключается в том, что он сочетает в себе эффективность нанесения и проникновения.

Доказательство с 409 страницы:
Дано уравнение:

−qxy(x)+d2dx2y(x)=0 – это уже преобразованное уравнение с 409 страницы первого порядка

Это дифференциальное уравнение имеет вид:

f1(x)*g1(y')*y'' = f2(x)*g2(y'),

где:

f1(x)=1

g1(y′)=1

f2(x)=xy(x))

g2(y′)=q

Приведём уравнение к виду:

g1(y')/g2(y')*y''= f2(x)/f1(x).

Разделим обе части уравнения на g2(y') и получим:

d2dx2y(x)q=xy(x)

Этим самым мы разделили переменные x и y'. Теперь домножим обе части уравнения на dx, тогда уравнение будет таким:

dxd2dx2y(x)q=dxxy(x)

или

dy′q=dxxy(x)

Возьмём от обеих частей уравнения интегралы: - от левой части интеграл по y', - от правой части интеграл по x.

∫1qdy′=∫xy(x)dx∫1

Возьмём эти интегралы

y′q=Const+∫xy(x)dx

Мы получили обыкн. уравнение с неизвестной y'.

(Const - это константа)

Решением будет:

y′(x)=C1+q∫xy(x)dxy′⁡

Возьмём эти интегралы:

∫d0+1dxy(x)dx=∫(C1+q∫xy(x)dx)dx∫

y(x)=C2+∫(C1+q∫xy(x)dx)dx

В итоге система преобразований говорит о том что система приводится к упрощённому виду с целью того, чтобы решить данную систему через интегрирование системы первого порядка.
СПИСОК ЛИТЕРАТУРЫ
1. Вазов,В. Асимптотическое разложение решений обыкновенных дифференциальных уравнений /В.Вазов - М.: Мир, 1968.

2. Зайцев,В.Ф. Справочник по обыкновенным дифференциальным уравнениям / В.Ф.Зайцев,А.Д.Полянин -М.: Физматлит, 2001. - 576 с.

3. Калинин, В.В. Обыкновенные дифференциальные уравнения (пособие для практических занятий) / В.Ф.Калинин - Издательство ФГУП "Нефть и газ" Российский государственный университет нефти и газа им. Губкина, 2005. Страница 68

4. Камке,А. Справочник по обыкновенным дифференциальным уравнениям / А.Камке - М.: Наука, 1976.

5. Коддингтон, Э.А.Теория обыкновенных дифференциальных уравнений / Коддингтон Э.А.Н.Левинсон М.: ИЛ, 1958.

6. Краснов, М.Л.Обыкновенные дифференциальные уравнения: задачи и примеры с подробными решениями /М.Л.Краснов.А.И Киселев. Макаренко М.: Изд-во УРСС, 2002. Страница 256

7. Кузьмина,Р.П. Асимптотические методы для обыкновенных дифференциальных уравнений /Р.П.Кузьмина -М.: Унифицированный УРСС, 2003.

8. Матвеев, Н. и др.Методы интегрирования обыкновенных дифференциальных уравнений. /Н.Матвеев-М.: Высшая школа, 1967.-557

---

Метод возмущения /А.Найфе - М.: Мир, 1976.

9. Пантелеев,А.В. Примеры и обыкновенные дифференциальные уравнения в задачах / А.В.Пантелеев,А.С.Якимова,А.В.Босов-М.: Издательство МАИ, 2000.-380

10. Понтрягин Л.С. Асимптотическое поведение решений систем дифференциальных уравнений с меньшими параметрами при более высоких производных, Труды Академии наук СССР, серия metem, 21 (1957).

11. Пушкарь Е.А. Дифференциальные уравнения: Учебное пособие. - М.: МГИУ, 2007. Страница 254

12. Рапопорт, И.М.О некоторых асимптотических методах в теории дифференциальных уравнений / И.М.Рапопорт – Киев: Академия наук Украинской ССР, 1954.

13. Рапопорт И.М.Асимптотическое ПОВЕДЕНИЕ РЕШЕНИЙ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ, ДАН СССР, КИЕВ, 1951

Самойленко,А.М. Дифференциальные уравнения: примеры и задачи / А.М.Самойленко, С.А.Кривошея,Н.А. Перестюк –М.: Высшая школа, 1989. Страница 383

14. Тамаркин Д.О некоторых общих задачах теории обыкновенных линейных дифференциальных уравнений и разложении любой функции в ряды / Я.Д.Тамаркин Санкт-Петербург, 1971

15. Федорюк,М.В. Асимптотический метод линейных обыкновенных дифференциальных уравнений /М.В.Федорюк –М.: Наука, 1983.

16. Фещенко, С.Ф.Асимптотический метод в разработке линейных дифференциальных уравнений / С.Ф.Фещенко, Н.И.Шкиль, Л.А.Д.Николенко - Киев: Научная думка, 1966.

17. Хартман Ф.Обыкновенные дифференциальные уравнения. - М.: Мир, 1970.

Эльшольц, Л.Е. Исчисление дифференциальных уравнений и вариаций / Л.Е.Эльшольц - М.: Наука, 1969. Страница 424

---

Смотрите также файлы

• 1. основы маркетинга лекция методологические основы дисциплины МАркетинг. Часть 1.pdf

• Информационный лист для учебного занятия, реализуемого с применением дистанционных образовательных технологий и электронного обучения.doc

• Пример задания 1.doc

• Дисциплина Безопасность жизнедеятельности Раздел Теоретические основы безопасности жизнедеятельности Тема Объект, предмет, методология, теория и практика безопасности.doc

• Задание Решите ситуационную задачу, используя предложенную методику.docx