Файл: Введение Разработка математической модели исходной сау.doc

СодержаниеВведение……………………………………………………………………………..4

1. 
   Разработка математической модели исходной САУ………………...………..5
   
2. 
   Анализ качества исходной САУ....................................…...……………….......8
   
3. 
   Синтез корректирующих устройств..................................................................11
   
4. 
   Анализ качества скорректированной САУ...................…………...……….....13
   
5. 
   Анализ точности САУ........................................................................................16
   
6. 
   Расчет параметров корректирующих устройств.........…..…………………...18
   

Заключение ………………………………………………………………………...21Список использованных источников……………………………………………..22Приложение А

Введение

Теория автоматического управления (ТАУ) изучает методы управления технологическими процессами, общие принципы построения систем автоматического управления (САУ), их расчета, математического моделирования, исследования и настройки. Целью управления является обеспечение требуемого течения процесса в объекте или требуемого изменения его состояния.Целью выполнения курсовой работы по ТАУ является освоение теоретических методов и получение навыков по применению технологии моделирования сложных систем управления.Задачи решаемые в курсовой работе :

1. 
   анализ качества исходной САУ;
   
2. 
   синтез методом оптимальных настроек регулятора;
   
3. 
   анализ качества спроектированной САУ;
   
4. 
   анализ точности спроектированной САУ;
   

Выполнение курсовой работы предусматривает получение дифференциального уравнения и передаточной функции объекта управления и его кривой разгона, исследование устойчивости САУ и качества регулирования.

1. Разработка структурной схемы и математической модели САУ

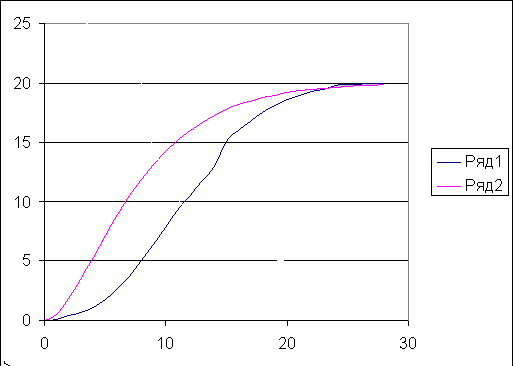
Построим кривую разгона по данным из приложения А таблицы А1 в соответствии с вариантом 1.1. [1, стр. 14]Рисунок 1 – Заданная кривая разгонаИсходные данные:

1. 
   требуемое время регулирования t_p=30,
   
2. 
   допустимое динамическое отклонение регулируемого параметра от установившегося значения ₁ = 10,
   
3. 
   величина внешнего возмущающего воздействия  = 0,6.
   

---

Для нахождения передаточной функции разомкнутой системы W(p) аппроксимируем исходную кривую разгона. 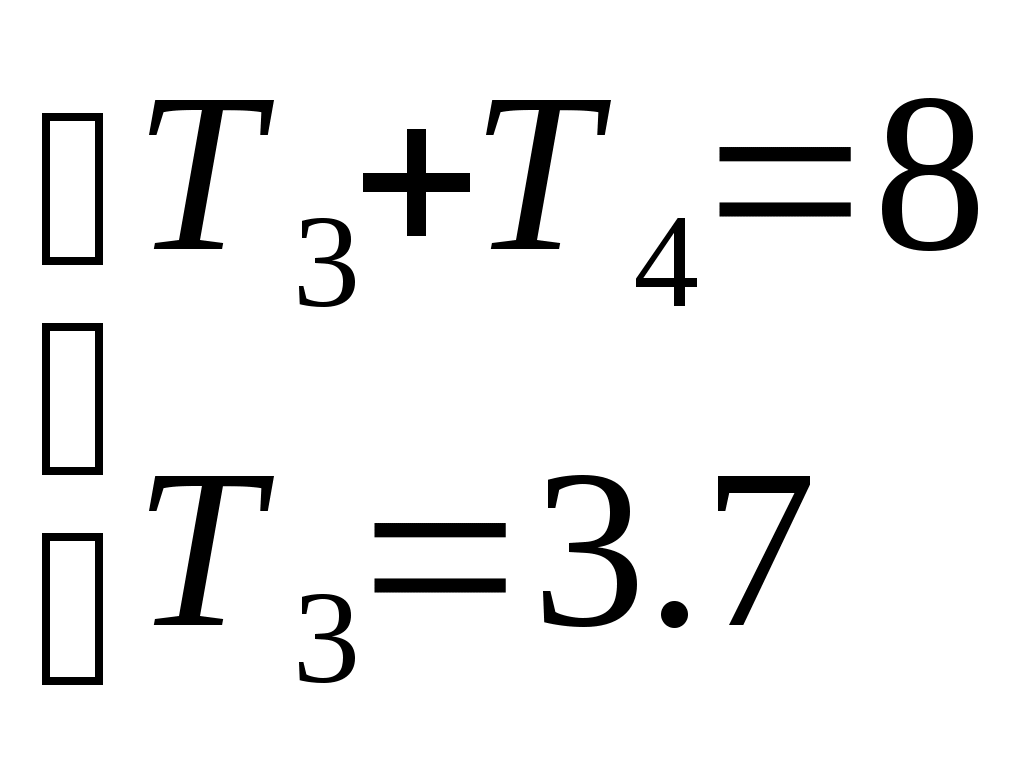Для аппроксимации можно выбрать апериодическое звено 2-го порядка или звено чистого запаздывания.Выберем апериодическое звено 2 порядка, так как оно обеспечивает хороший запас устойчивости по амплитуде и по фазе.Передаточная функция апериодического звена 2 порядка имеет вид:Для нахождения значений параметров Т₃и Т₄составим систему уравнений:Решив систему уравнений, получим: Т₃ = 3,7 и Т₄ = 4,3с.Коэффициент усиления К=20.Таким образом, получили передаточную функцию разомкнутой системы: ;Построим кривую разгона по полученной передаточной функции.Рассчитаем среднеквадратичное отклонение полученной кривой разгона от заданной: ,где у_з – заданное значение выходной координаты;у_р – рассчитанное значение выходной координаты;N – число экспериментальных точек.Значение sigma не должно превышать 10.Для полученных значений можно записать:Полученное значение sigma меньше 10, значит, кривую разгона можно выразить полученной нами передаточной функцией разомкнутой системы:ω₁=1/Т₁=0.27 (lg0.27=-0.57 1/c)ω₂=1/Т₂= 0.23lg= 0.23=-0.63 1/c)Структурная схема представленной САУ изображена на рисунке 2, где W₁ – устройство управления: W₂ – объект управления: 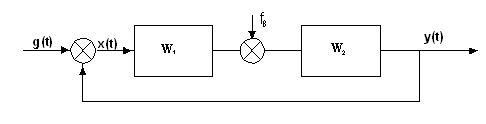Рисунок 2 – Структурная схема исходной САУ

2 Анализ качества исходной САУ

---

1. 
   Главная передаточная функция замкнутой системы:
   

2. 
   Передаточная функция по возмущению:
   

Анализ качества системы автоматического управления принято оценивать с помощью следующих показателей – времени регулирования, величины перерегулирования, значения ошибки в установившемся режиме, точности, и числа колебаний регулируемой величины за время переходного процесса.Интервал времени, по истечении которого отклонение переходной характеристики от установившегося значения не превышает величины d = 5%, называется временем регулирования t_p. Время регулирования является основной характеристикой быстродействия системы, т.е. 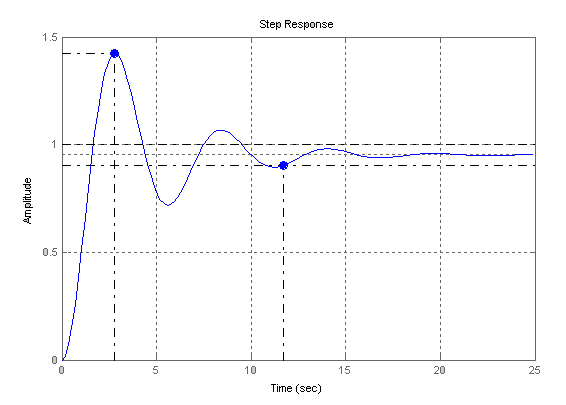определяет длительность переходного процесса.Рисунок 4 – График главной передаточной функции исходной САУАнализируя главную передаточную функцию замкнутой системы Ф(р) (рисунок 3), с помощью программного пакета MATLAB, получили следующие характеристики:Время регулирования t_р = 11,7с.Величина перерегулирования .Определим запасы по фазе и амплитуде исходной САУ, используя графики логарифмических частотных характеристик (рисунок 4).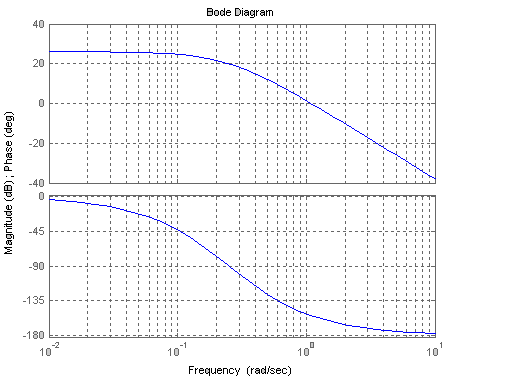5 – ЛФЧХ и ЛАЧХ главной передаточной функции исходной САУЗапас по фазе: Δφ(ω)= 28 град.Запас по амплитуде: ΔL(ω) обеспечен.Построим график передаточной функции по возмущению (рисунок 5 ):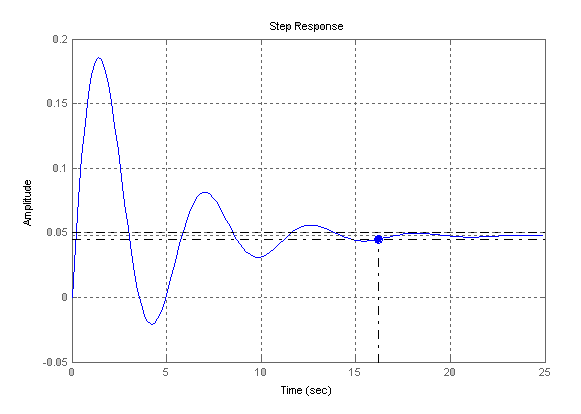Рисунок 6 – Кривая переходного процесса по возмущениюВремя регулирования t_р=16,2 с.В таблице 1 приведены показатели исходной и желаемой САУ.Таблица 1

Показатели качества	Перерегулирование σ , %	Время переходного процесса tp	Коэффициент усиления K
Желаемые	30	30	33.3
Полученные	49.4	11.7	20

---

Из анализа качества системы автоматического управления видно, что исходная система не удовлетворяет заданным показателям качества. Повысить качество процесса регулирования можно с помощью синтеза САУ, то есть необходимо изменить динамические свойства системы регулирования с помощью корректирующих устройств.

3 Синтез корректирующих устройств

Повысить качество процесса регулирования можно с помощью синтеза САУ, т.е. изменяя динамические свойства системы регулирования с помощью корректирующих устройств. Динамические свойства системы автоматического регулирования можно улучшить как последовательными, так и параллельными включениями корректирующих устройств.Рассмотрим синтез САУ с помощью охватывания звеньев с наихудшими показаниями обратной связью с корректирующим устройством. Построим ЛАЧХ для исходной системы и для желаемой. Строим ЛАЧХ для располагаемой САУ (приложение А): На высоте проводим прямую 0 дБ/дек начиная слева и до частоты . Затем от этой точки в том же направлении проводим прямую с наклоном -20 дБ/дек до частоты . Далее от этой точки проводим прямую с наклоном –40 дБ/дек. Строим ЛАЧХ для желаемой САУ (приложение А): ЛАЧХ желаемой системы должна соответствовать требованиям качества переходного процесса. Для ее построения, зная желаемое время переходного процесса(t_р=15с) определим необходимую частоту среза ω_ср по формуле: с^-1,где – число полуколебаний в процессе. Я взяла .На частоте среза в области сопряженных частот будет наклон ЛАЧХ -20 дБ/дек. Протяженность среднечастотной части желаемой ЛАЧХ рассчитывается по формулам:

---

, , (5)где M – показатель колебательности. Я выбрала М=2,25.В своей курсовой работе я подбирала такие и М, чтобы скорректированная система удовлетворяла параметрам желаемой САУ.ω_c1 = ω_с(M+1)/M =0,24(1.5 + 1)/1.5 = 0.35 с^-1,ω_c2 = ω_с(M-1)/M = 0,24 (1.5 - 1)/1.5 = 0,05 c^-1,где М = 1,5 – показатель колебательности:Находим по формулам (5) и : , т.е. с, с^-1, , т.е. с, с^-1.Я выбрала такие сопряженные частоты, с, с^-1, , с, с^-1, .Построив ЛАЧХ исходной и желаемой систем, стоим ЛАЧХ корректирующего устройства: .Определяем по графику передаточную функцию последовательного корректирующего устройства: . находим по графику:

---