Файл: Введение Разработка математической модели исходной сау.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 91
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.

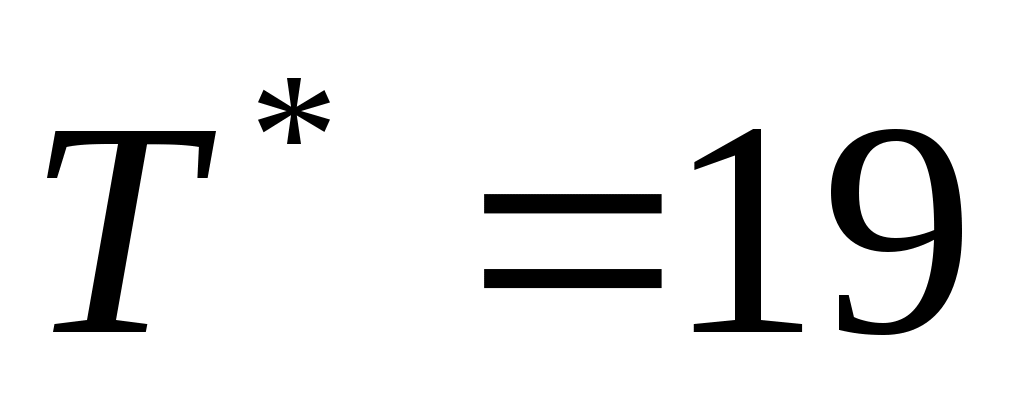 с определили по ЛАЧХ исходной и желаемой систем, так как
с определили по ЛАЧХ исходной и желаемой систем, так как 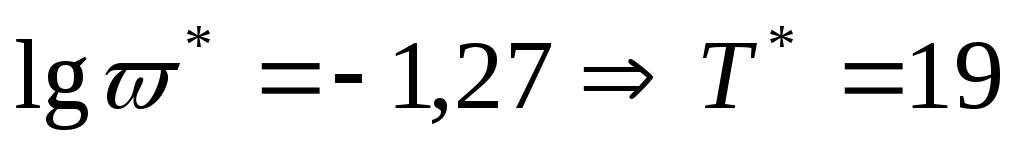 с.
с.
Запишем передаточную функцию желаемой разомкнутой системы, зная, что
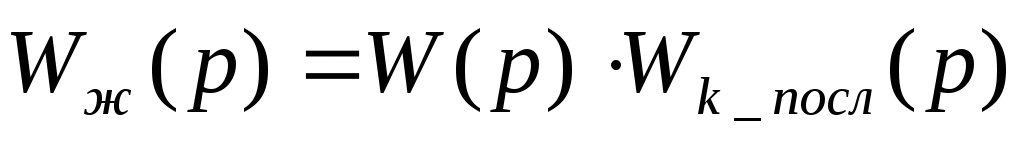 .
.
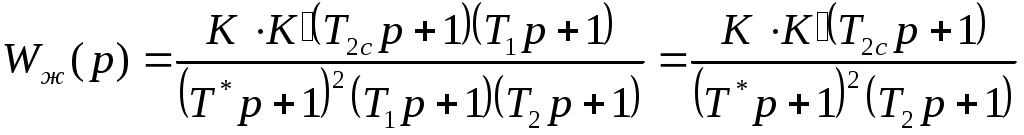 (6)
(6)
Определим эту же функцию по графику: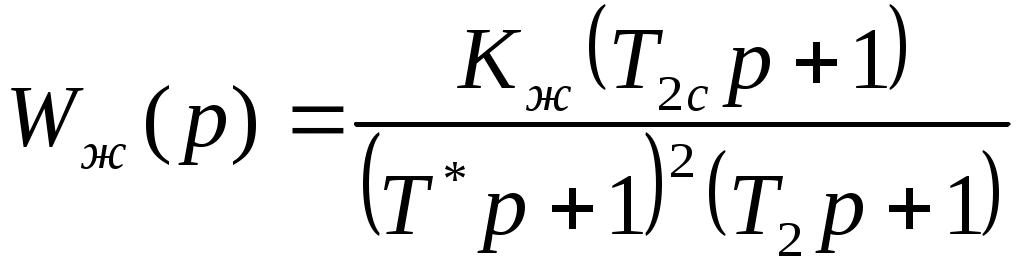 , (7)
, (7)
где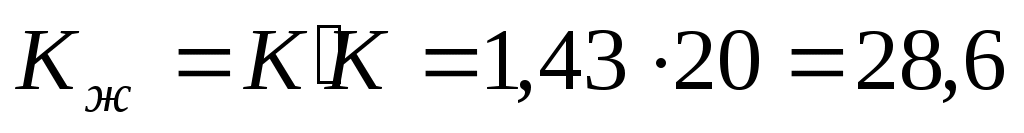 .
.
Исходя из того, что выражения (6) и (7) равны, можно сделать вывод, что является передаточной функцией скорректированной системы.
является передаточной функцией скорректированной системы.
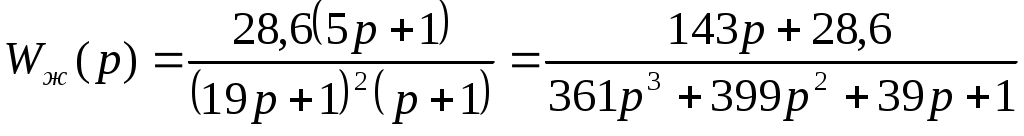 .
.
Найдем передаточную функцию самого корректирующего устройства.
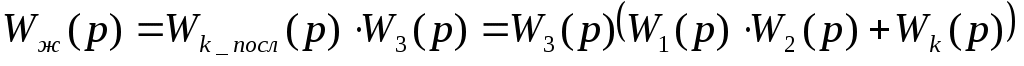

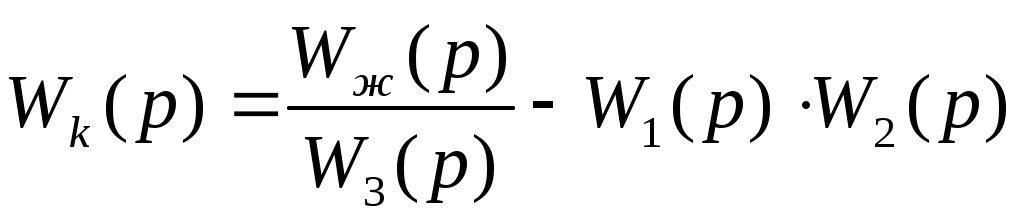
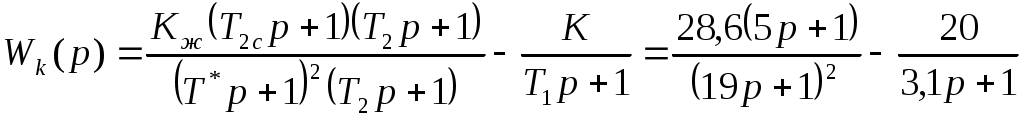 .
.
Проделав математические преобразования, получаем:
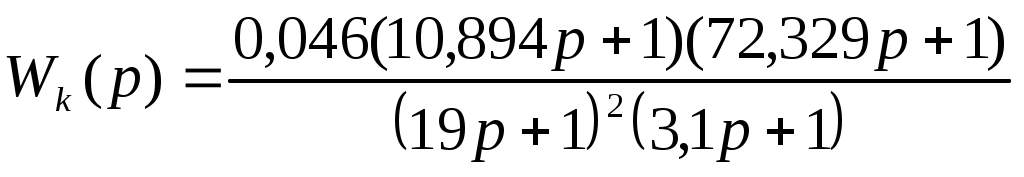 .
.
Построение исходной ЛАЧХ происходит вычитанием из располагаемой желаемой ЛАЧХ:
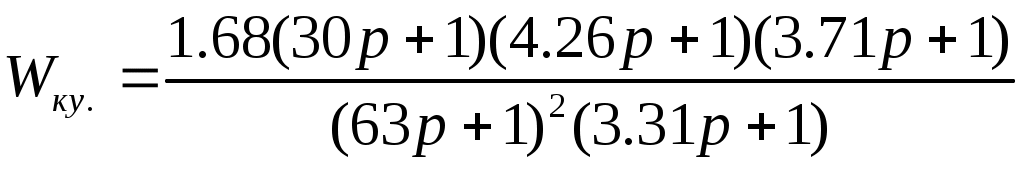
Передаточная функция скорректированной системы имеет вид определяется по формуле: ,
,
где Wск – передаточная функция скорректированной системы.
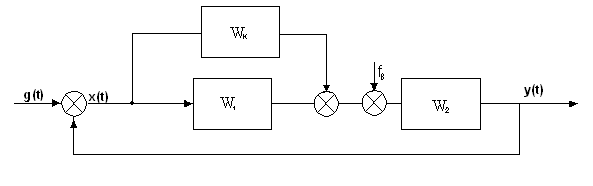
Рисунок 7 – Структурная схема желаемой САУ (с параллельной коррекцией)

Анализ качества скорректированной системы автоматического управления произведем таким же образом, как и в случае исходной системы. Для этого будем использовать показатели качества (время регулирования tp и величину перерегулирования σ). Для этого построим переходные характеристики скорректированной САУ. Запасы устойчивости по фазе и по амплитуде определим по логарифмическим характеристикам САУ.
Передаточная функция для скорректированной системы:
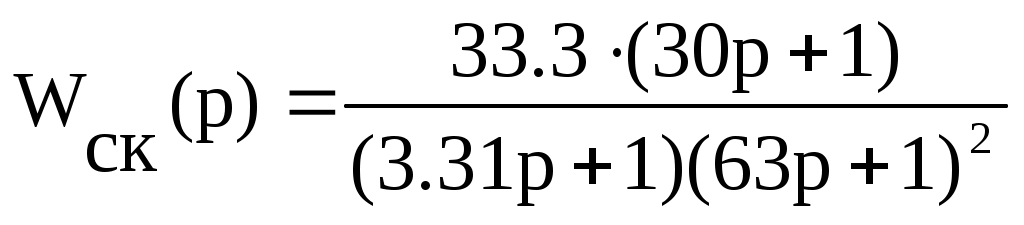 .
.
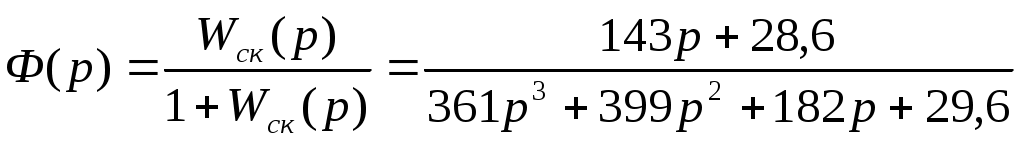
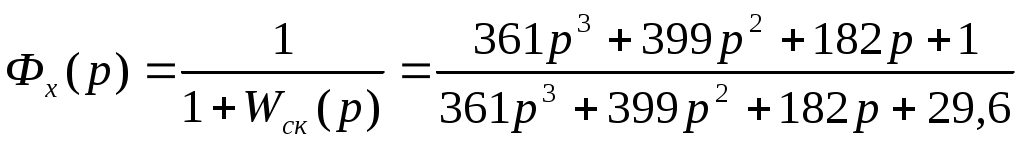
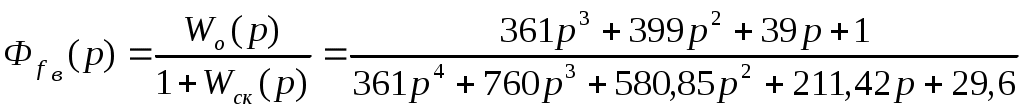
Анализируя главную передаточную функцию скорректированной замкнутой системы (рисунок ), получили следующие характеристики:
(рисунок ), получили следующие характеристики:
Время регулирования tр =30 с.
Величина перерегулирования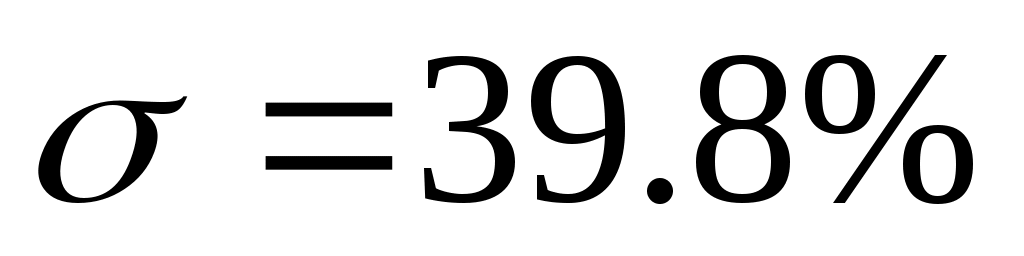 .
.
Передаточная функция скорректированной САУ по возмущению (рисунок):
Проанализировав полученные кривые, заключаем, что скорректированная система удовлетворяет заданным показателям качества и обеспечивает следующие запасы устойчивости, по амплитуде L обеспечен, по фазе = 83,50
Таблица 2
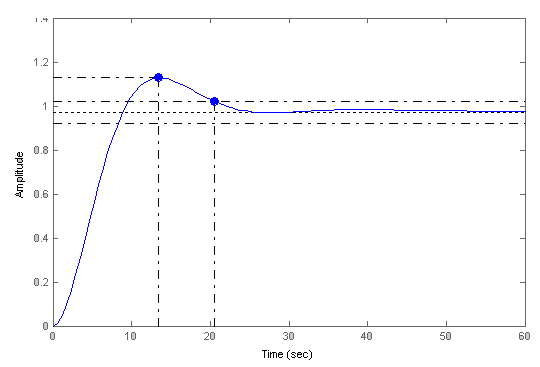
Рисунок 8 – График переходного процесса скорректированной САУ
Время регулирования tр =16,2 с.
Величина перерегулирования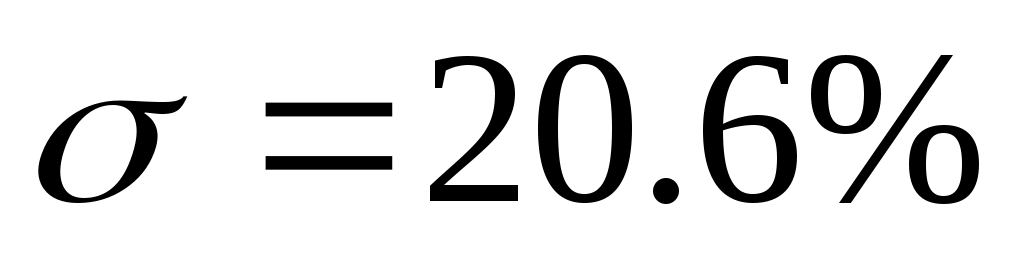 .
.
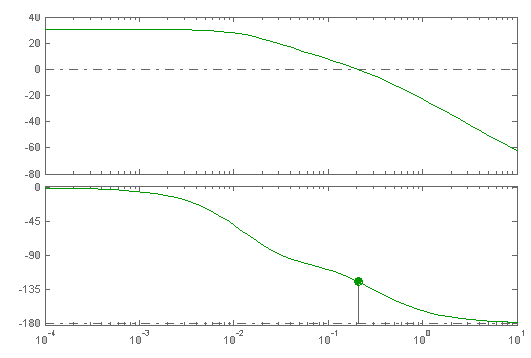

Рисунок 9 - ЛАЧХ и ЛФЧХ скорректированной САУ.
Запас по фазе: ж() = 550.
Запас по амплитуде: Lж() обеспечен.

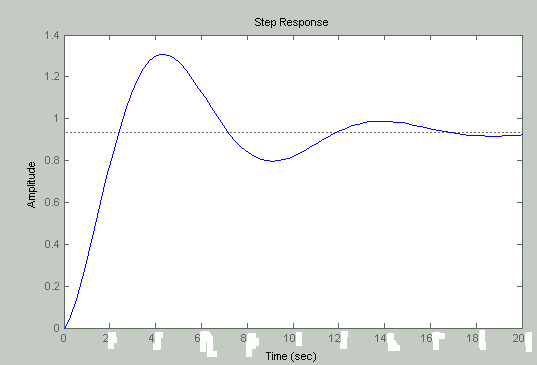
Рисунок10 - График передаточной функции по возмущению скорректированной САУ
Время регулирования tр =15,8 с.
Разбиваем передаточную функцию корректирующего устройства (формула 4.6) на типовые корректирующие звенья.
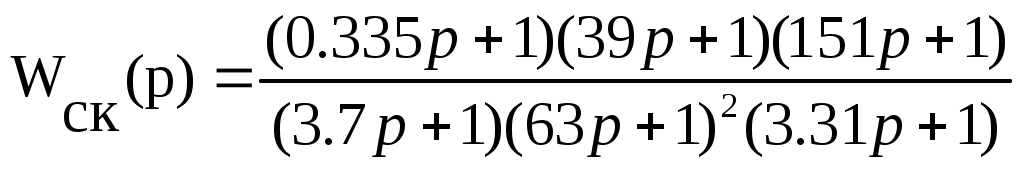
В результате получаем, что корректирующее устройство реализуется последовательным соединением трех звеньев .
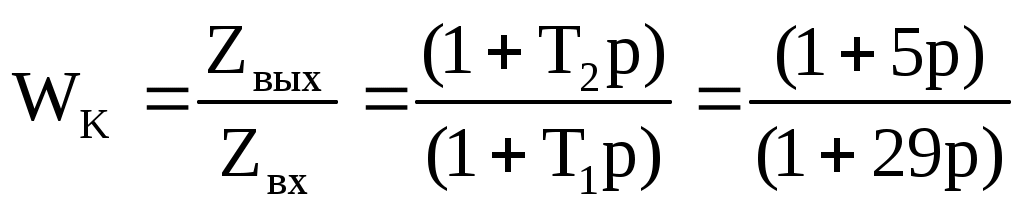 ;
;
где Т1=(R0+R1)C1; T2=R1C1; [4]
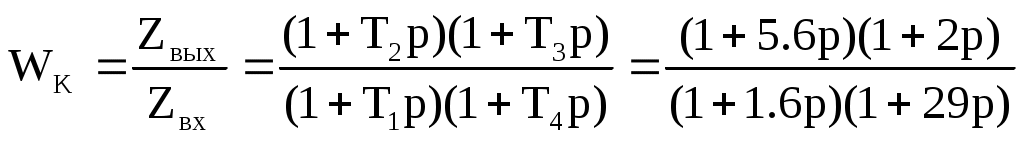 ;
;
где Т1=(R2+R3)C3; T2=R3C3; T3=R2C2; T4=(R2//R3)C2; [4]
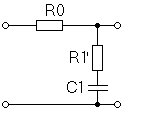
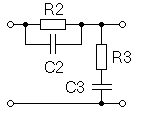
рис.6.1 рис.6.2
При расчете следует руководствоваться правилом согласования входных и выходных импедансов : Rвх = 10Rвых,
где Rвых– выходное сопротивление предыдущего контура,
Rвх
– входное сопротивление рассчитываемого контура.
При расчете первого звена принимаем выходное сопротивление предыдущего контура Rвых=100 Ом, а Rвх=R0=1000 Ом (ωср=0.4 с-1).
Далее выходное сопротивление рассчитывается по формуле 6.1.
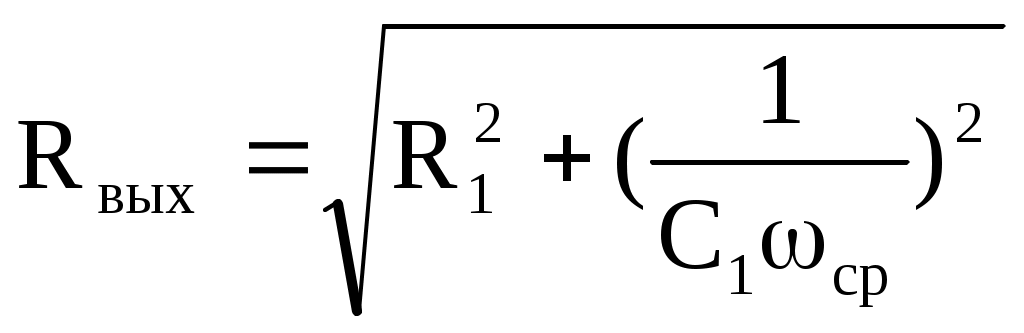 , (6.1)
, (6.1)
Определим номиналы элементов корректирующего устройства для звеньев (Рис. 6.1, 6.2) :
1)Для пассивного интегрирующего звена:
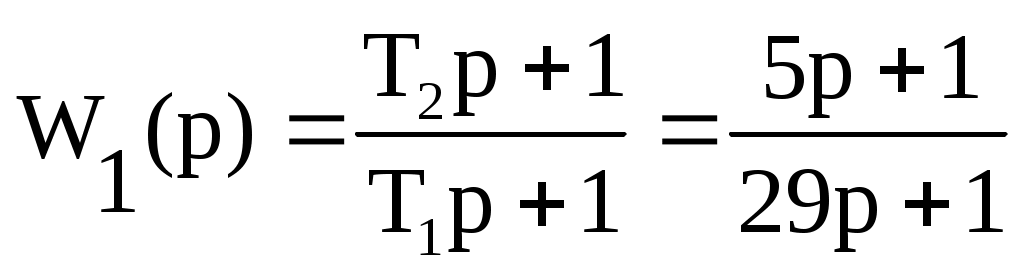
Т1=(R0+R1)C1; (6.2)
T2=R1C1; (6.3)
где T2 = 5 с;
Т1 = 29 с.
Рассчитаем номиналы звена:
С1 рассчитывается из условия

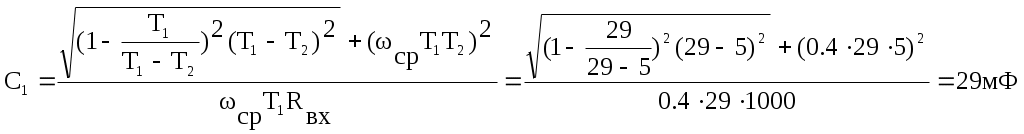
Откуда получим
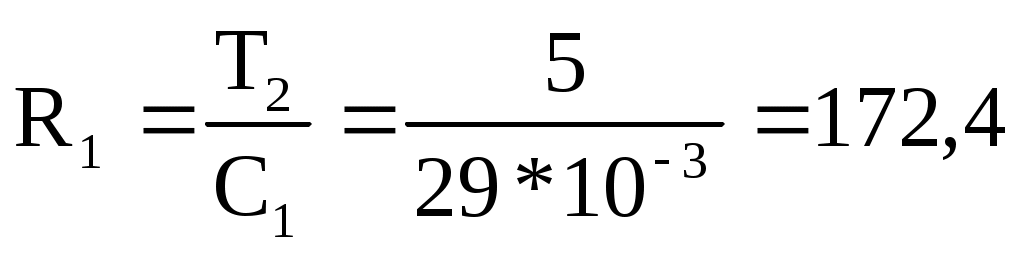 Ом,
Ом,
По формуле (6.1) определяем выходное сопротивление звена:
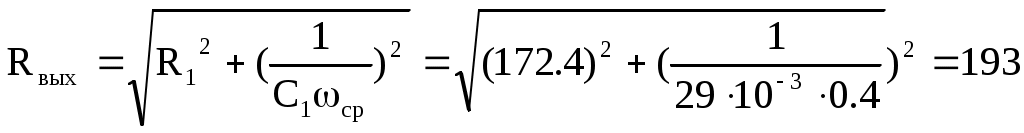 Ом
Ом
2) Аналогично рассчитываются параметры пассивного интегро-дифференцирующего звена
R2=Rвх(1+2*ωср)=347.4 Ом, C3=(T1-T2)/R2=(5.6-1.6)/347.4=11.5 мФ,
C2 =T3/R2=2/347.4=5.8 мФ, R3 =T2/C3=1.6/0.0115=138.96 Ом,
Для получения требуемого коэффициента усиления в цепь включается усилитель:
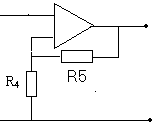
Рисунок 6.3 – Неинвертирующий операционный усилитель с обратной связью
Для Кку=1.67 рассчитаем неинвертирующий операционный усилитель с обратной связью (рис. 6.2).
 По формуле 6.1 получили R4 =258 Ом. Сопротивление R5 определим из следующего соотношения:
По формуле 6.1 получили R4 =258 Ом. Сопротивление R5 определим из следующего соотношения:
R5 =(К ку- 1)*R4 = (1.67-1)*258 = 172.86 Ом.
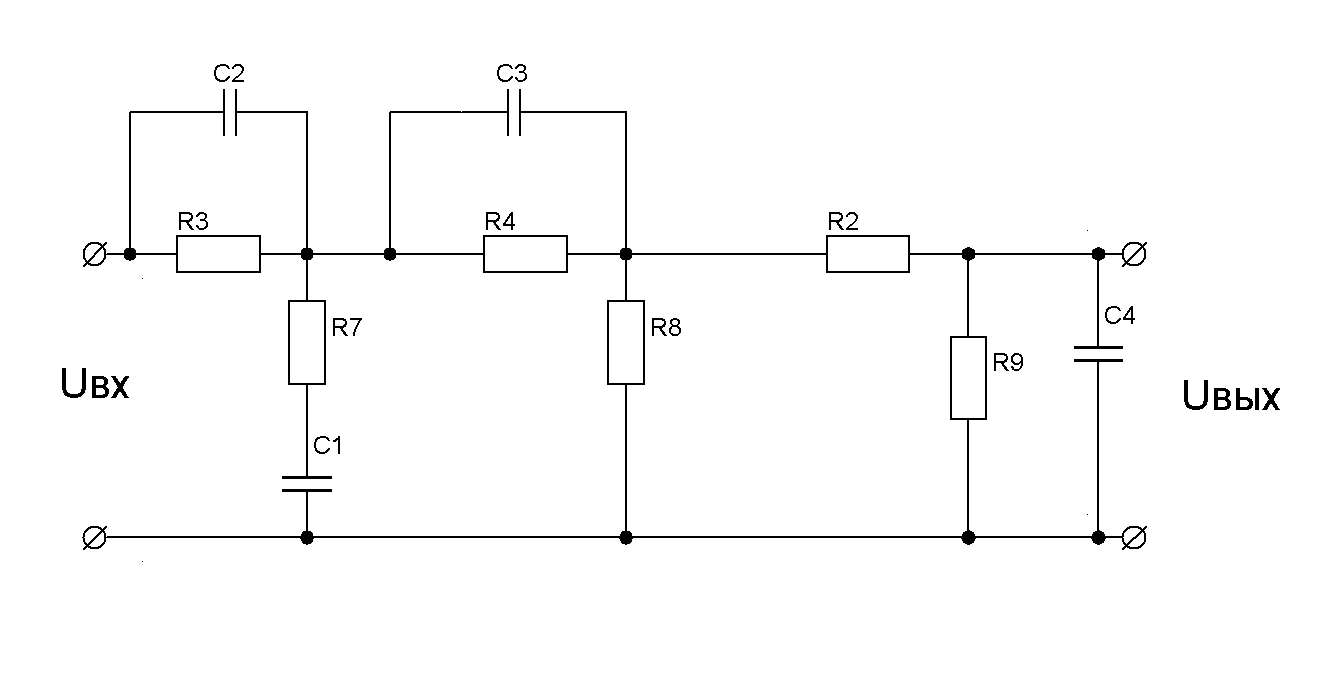
Рисунок 11-Электрическая схема корректирующего устройства
Точность системы задается и определяется в установившихся режимах.
Передаточная функция по ошибке для располагаемой системы имеет вид:
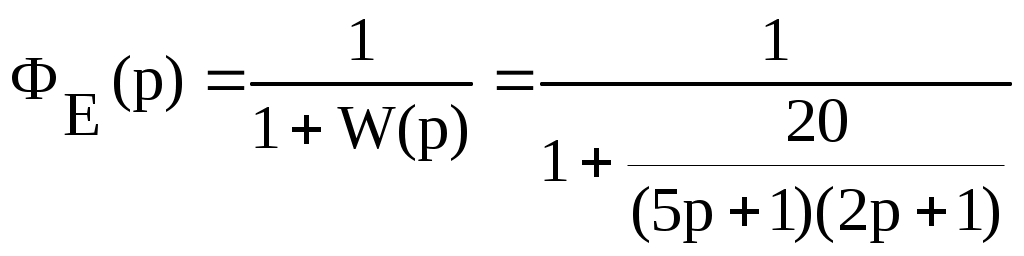 ; (7.1)
; (7.1)
Передаточная функция по ошибке для скорректированной системы
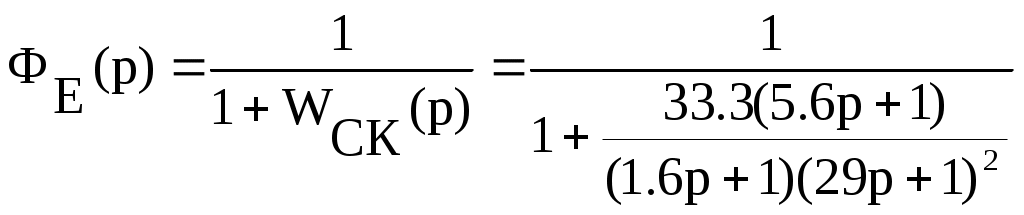 ; (7.2)
; (7.2)
По передаточной функции по ошибке мы можем определить скоростную ошибку (ЕСК). Скоростная ошибка – это ошибка системы, которая при задающем воздействии с постоянной скоростью не будет нарастающей. График передаточной функции по ошибке располагаемой системы показан на рисунке 7.1, а системы после коррекции – на рисунке 7.2. Из графиков определяем, что ошибка располагаемой САУ составляет 0.085, а скорректированной САУ равна 0.06.
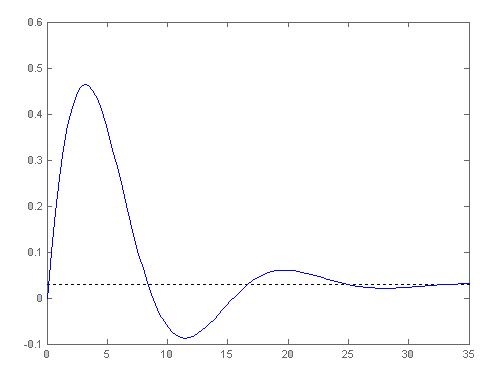
Рисунок 12 – Функция по ошибке располагаемой САУ
Е = 0.046
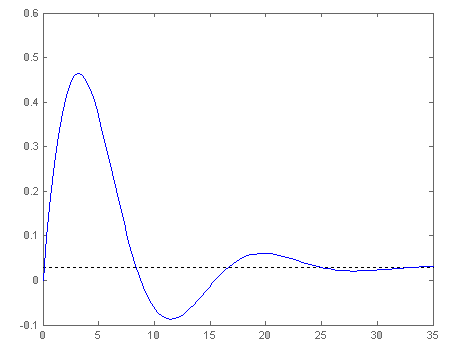

Рисунок 13 – Функция по ошибке скорректированной САУ
Е = 0.0116
Цель, поставленная перед нами, в курсовом проекте достигнута.
В ходе выполнения курсовой работы было получено дифференциальное уравнение и передаточная функция объекта управления и его кривая разгона, исследована устойчивость САУ. Так как система не удовлетворяла заданным показателям качества, был проведен синтез системы методом ЛАЧХ, задачей которого было подобрать последовательное корректирующее устройство, при котором система удовлетворяла заданным требованиям к ее качеству.
В результате коррекции:
Т.о. спроектированная система удовлетворяет всем заданным требованиям.

Запишем передаточную функцию желаемой разомкнутой системы, зная, что
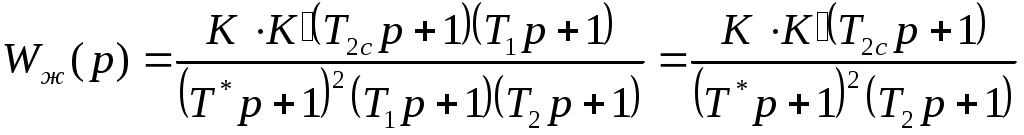 (6)
(6)Определим эту же функцию по графику:
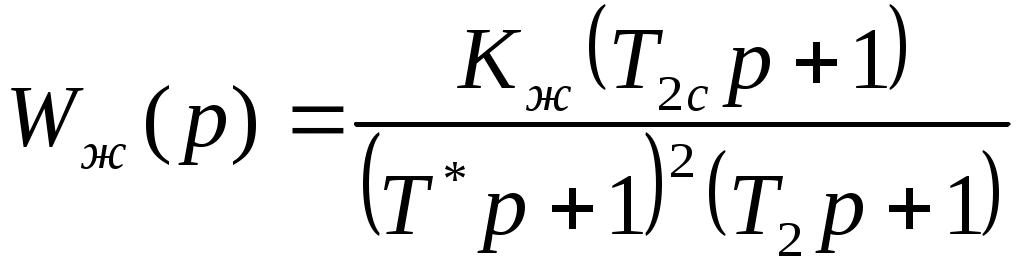 , (7)
, (7)где
Исходя из того, что выражения (6) и (7) равны, можно сделать вывод, что
Найдем передаточную функцию самого корректирующего устройства.
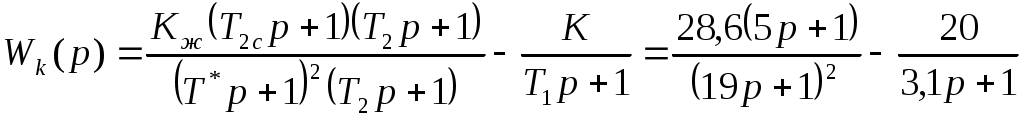 .
.Проделав математические преобразования, получаем:
Построение исходной ЛАЧХ происходит вычитанием из располагаемой желаемой ЛАЧХ:
Передаточная функция скорректированной системы имеет вид определяется по формуле:
где Wск – передаточная функция скорректированной системы.

Рисунок 7 – Структурная схема желаемой САУ (с параллельной коррекцией)

 4 Анализ качества скорректированной САУ
4 Анализ качества скорректированной САУ
Анализ качества скорректированной системы автоматического управления произведем таким же образом, как и в случае исходной системы. Для этого будем использовать показатели качества (время регулирования tp и величину перерегулирования σ). Для этого построим переходные характеристики скорректированной САУ. Запасы устойчивости по фазе и по амплитуде определим по логарифмическим характеристикам САУ.
Передаточная функция для скорректированной системы:
-
Главная передаточная функция:
-
Передаточная функция по ошибке:
-
Передаточная функция по возмущению:
Анализируя главную передаточную функцию скорректированной замкнутой системы
Время регулирования tр =30 с.
Величина перерегулирования
Передаточная функция скорректированной САУ по возмущению (рисунок):
Проанализировав полученные кривые, заключаем, что скорректированная система удовлетворяет заданным показателям качества и обеспечивает следующие запасы устойчивости, по амплитуде L обеспечен, по фазе = 83,50
Таблица 2
| САУ/Параметры | tр , с | σ, % | , град | L, дБ |
| Желаемая | 12 | 42 | >40 | 16…20 |
| Экспериментальная | 11.3 | 39.8 | 83.5 | обеспечен |

Рисунок 8 – График переходного процесса скорректированной САУ
Время регулирования tр =16,2 с.
Величина перерегулирования


Рисунок 9 - ЛАЧХ и ЛФЧХ скорректированной САУ.
Запас по фазе: ж() = 550.
Запас по амплитуде: Lж() обеспечен.


Рисунок10 - График передаточной функции по возмущению скорректированной САУ
Время регулирования tр =15,8 с.
-
 Расчет элементов корректирующего устройства
Расчет элементов корректирующего устройства
Разбиваем передаточную функцию корректирующего устройства (формула 4.6) на типовые корректирующие звенья.
В результате получаем, что корректирующее устройство реализуется последовательным соединением трех звеньев .
-
Интегрирующе-дифференцирующее звено (рис. 6.1)
где Т1=(R0+R1)C1; T2=R1C1; [4]
-
Пассивное интегро-дифференцирующее звено (рис.6.2)
где Т1=(R2+R3)C3; T2=R3C3; T3=R2C2; T4=(R2//R3)C2; [4]


рис.6.1 рис.6.2
При расчете следует руководствоваться правилом согласования входных и выходных импедансов : Rвх = 10Rвых,
где Rвых– выходное сопротивление предыдущего контура,
Rвх
– входное сопротивление рассчитываемого контура.
При расчете первого звена принимаем выходное сопротивление предыдущего контура Rвых=100 Ом, а Rвх=R0=1000 Ом (ωср=0.4 с-1).
Далее выходное сопротивление рассчитывается по формуле 6.1.
Определим номиналы элементов корректирующего устройства для звеньев (Рис. 6.1, 6.2) :
1)Для пассивного интегрирующего звена:
Т1=(R0+R1)C1; (6.2)
T2=R1C1; (6.3)
где T2 = 5 с;
Т1 = 29 с.
Рассчитаем номиналы звена:
С1 рассчитывается из условия

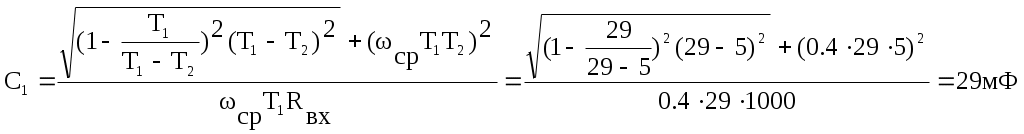
Откуда получим
По формуле (6.1) определяем выходное сопротивление звена:
2) Аналогично рассчитываются параметры пассивного интегро-дифференцирующего звена
R2=Rвх(1+2*ωср)=347.4 Ом, C3=(T1-T2)/R2=(5.6-1.6)/347.4=11.5 мФ,
C2 =T3/R2=2/347.4=5.8 мФ, R3 =T2/C3=1.6/0.0115=138.96 Ом,
Для получения требуемого коэффициента усиления в цепь включается усилитель:

Рисунок 6.3 – Неинвертирующий операционный усилитель с обратной связью
Для Кку=1.67 рассчитаем неинвертирующий операционный усилитель с обратной связью (рис. 6.2).
 По формуле 6.1 получили R4 =258 Ом. Сопротивление R5 определим из следующего соотношения:
По формуле 6.1 получили R4 =258 Ом. Сопротивление R5 определим из следующего соотношения:R5 =(К ку- 1)*R4 = (1.67-1)*258 = 172.86 Ом.

Рисунок 11-Электрическая схема корректирующего устройства
-
 АНАЛИЗ ТОЧНОСТИ САУ
АНАЛИЗ ТОЧНОСТИ САУ
Точность системы задается и определяется в установившихся режимах.
Передаточная функция по ошибке для располагаемой системы имеет вид:
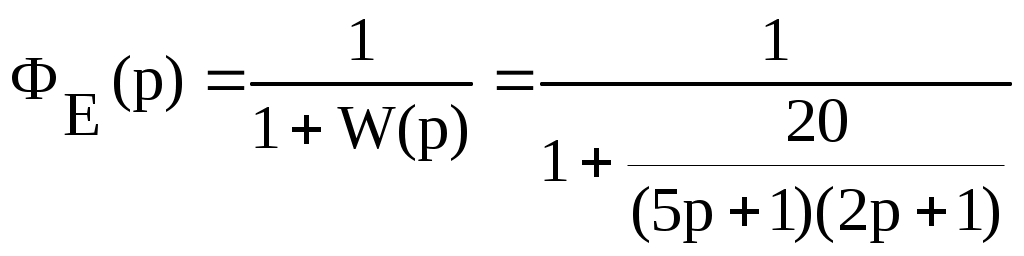 ; (7.1)
; (7.1)Передаточная функция по ошибке для скорректированной системы
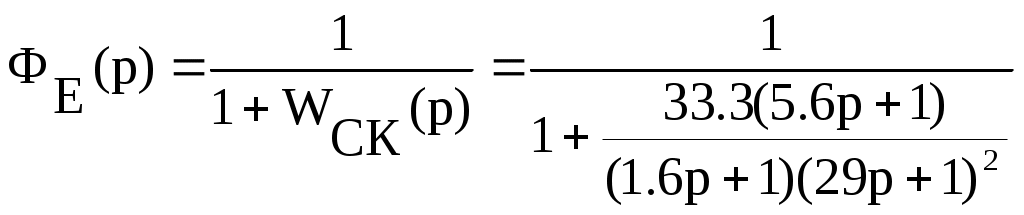 ; (7.2)
; (7.2) По передаточной функции по ошибке мы можем определить скоростную ошибку (ЕСК). Скоростная ошибка – это ошибка системы, которая при задающем воздействии с постоянной скоростью не будет нарастающей. График передаточной функции по ошибке располагаемой системы показан на рисунке 7.1, а системы после коррекции – на рисунке 7.2. Из графиков определяем, что ошибка располагаемой САУ составляет 0.085, а скорректированной САУ равна 0.06.

Рисунок 12 – Функция по ошибке располагаемой САУ
Е = 0.046


Рисунок 13 – Функция по ошибке скорректированной САУ
Е = 0.0116
 ЗАКЛЮЧЕНИЕ
ЗАКЛЮЧЕНИЕ
Цель, поставленная перед нами, в курсовом проекте достигнута.
В ходе выполнения курсовой работы было получено дифференциальное уравнение и передаточная функция объекта управления и его кривая разгона, исследована устойчивость САУ. Так как система не удовлетворяла заданным показателям качества, был проведен синтез системы методом ЛАЧХ, задачей которого было подобрать последовательное корректирующее устройство, при котором система удовлетворяла заданным требованиям к ее качеству.
В результате коррекции:
-
показатели качества скорректированной САУ (время регулирования tp, величина перерегулирования σ) практически совпали с желаемыми (таблица 5.1); -
полученные запасы по амплитуде и по фазе удовлетворяют требованиям, предъявляемым к САУ по устойчивости; -
точность системы увеличилась (Е=0.085, Еск=0.06 ) .
Т.о. спроектированная система удовлетворяет всем заданным требованиям.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
Методические указания для студентов специальности Т.11.03 “Автоматизация технологических процессов и производств” (Кузьмин Б.П., Иванова И.Д., Волынская Е.Л.) Могилев, ротапринт МТИ, 2000г. -
Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989. -
Анхимюк В.Л. Теория автоматического управления. Мн.: Вышэйшая школа, 1979. -
Бесекерский В.А. , Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975.
