Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования
«Пермский национальный исследовательский

политехнический университет»

Аэрокосмический факультет

кафедра «Авиационные двигатели»

Специальность 24.05.02 (160700)

«Проектирование авиационных и ракетных двигателей».
О Т Ч Е Т

по практическим занятиям по дисциплине

ИНЖЕНЕРНО-ВЫЧИСЛИТЕЛЬНЫЕ ТЕХНОЛОГИИ

Выполнили студенты гр.АД-19-1С

___________________________________________

(подпись)

Проверил:


_____ст. преподаватель кафедры КОНЕВ И.П.________

(должность, Ф.И.О. преподавателя)

___________ _________________________

(оценка) (подпись)

_____________

(дата)

Пермь 2021

Лабораторная работа №1

Простейшие вычисления

ЗАДАНИЕ 1:

а) вычислить значение функции y =f(x) в точке х₀

(вар 4)

х₀ =4,21

х_n =7,6

>> x=4.21;

>> y=1/(x*(1-log(x)))-2

y = -2.5430

б) простроить график функции y =f(x) используя встроенную функцию MatLab poly(x,y) на интервале от х₀ до х_{n ,} шаг аргумента x определить самостоятельно
>> x=4.21:0.01:7.6;

>> y=1./(x.*(1-log(x)))-2

y = -2.5430 -2.5388 -2.5346 -2.5305 -2.5265 -2.5225 -2.5186

>> plot(x,y)



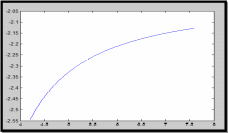
Рис.2 График функции

Вывод: MatLAB позволяет вычислять значение функции y =f(x) в точке х0 и строить графики с помощью встроенной функции poly(x,y).

---

Лабораторная работа №2

Символьные вычисления в MatLab
ЗАДАНИЕ 1:

Решить алгебраические уравнения, используя команду solve:



>> [x]=solve('1/(x+3)+(x+8)/(2*x^2-18)=1/(3-x)-1')

x =105^(1/2)/4 - 5/4

- 105^(1/2)/4 - 5/4

ЗАДАНИЕ 2:

Решить систему алгебраических уравнений, используя команду solve.



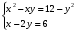
>> [ x, y ] = solve ('x^2-x*y=12-y^2', 'x-2*y=6')

x = 2, -2

y = -2, -4

ЗАДАНИЕ 3:
Упростить выражения, используя команду simplify:



>> syms c

>> p=(c/(c-2)-c/(c+2)-(c^2+4)/(4-c^2))*(2-c)^2/(2*c+c)

p = ((c - 2)^2*((c^2 + 4)/(c^2 - 4) + c/(c - 2) - c/(c + 2)))/(3*c)

>> simplify(p)

ans = (c^2 - 4)/(3*c)

ЗАДАНИЕ 4:

Вычислить сумму ряда, используя команду symsum.



>> syms k x

>> s=symsum((2*k)-1)^2/2^k/k, 3,10)

>> s=symsum((2*k-1)^2/2^k/k, 3,10)

s = 195155/64512

ЗАДАНИЕ 5:

Вычислить производную функции по х, используя команду diff.



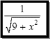
>> syms x

>> y=1/sqrt(9+x^2)

y =1/(x^2 + 9)^(1/2)

>> diff(y)

ans = -x/(x^2 + 9)^(3/2)

ЗАДАНИЕ 6:

Используя функцию int, подготовить и организовать вычисление определенного интеграла:



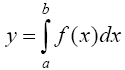
Подынтегральная функция f(x) определена и непрерывна на интервале a <= x <= b.



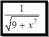
>> syms x a b

>> int(1/sqrt(9+x^2),0,2)

ans = log(13^(1/2)/3 + 2/3)

Вывод: MatLAB позволяет вычислять производные, интегралы, находить сумму ряда, упрощать выражения и т.д. с помощью специальных функций.

Лабораторная работа №3

Высокоуровневая графика в MatLAB

Цели работы:

1. Знакомство с основными возможностями высокоуровневой (high-level) графики MATLAB для отображения функций двух и трёх переменных, визуализации векторных и матричных данных и векторных полей.

Для выполнения данной лабораторной работы необходимо уметь работать с массивами — вектора­

---

ми и матрицами, понимать выполнение поэлементных операций с массива­ми.

Задание 1.

Построить графики функций. Использовать функцию plot. Нужно самостоятельно задать шаг и диапазон изменения аргумента

y = x^ 2 – 4 ;

y = x ^4 - 4x ^2 ;

y = sin (x) + log (x).

1)x= 3;

>> y= x^2 -4

y = 5

>> x = -10 : 0.05 :10 ;

>> y= x.^2 -4

y = plot(x,y)

Рисунок 1: График функции y = x^ 2-4



2) x= 5;

>> y= x^4 - 4*x^2

y = 525

>> x = -10 : 0.05 : 10 ;

>> y= x.^4- 4.*x.^2

y =plot(x,y)

Рисунок 2: График функции y= x^4- 4*x^2



3) x = 5;

>> y = sin(x)-log10(x)

y = -1.657894278999157

>> x= -10 :0.05 : 10;

>> y= sin(x)-log10(x)

y = plot(x,y)

Рисунок 3: График функции y = sin(x)-log10(x)

Задание 2.

Построить кривые, заданные параметрически. Использовать функцию plot.

Уравнение кривой: x (t) = t – sin (t) , y (t) = 1- cos (t)

– постройте эту кривую при t, изменяющимся в диапазоне [-π;π].

– постройте эту кривую при t, изменяющимся в диапазоне [0;2π].

a)

t = -pi:0.1:pi;

>> x = 1-sin(t);

>> y = 1- cos(t);

plot (x,y), grid, set(gcf,'color', 'white')



Рисунок 4: График функции x (t) = t – sin (t) , y (t) = 1- cos (t) [-π;π]



b)

Рисунок 5: График функции x (t) = t – sin (t) , y (t) = 1- cos (t) [0;2π]

Задание 3.

Построить кривые, заданные в полярной системе координат в диапазоне [0; 2π].

Использовать функцию polar.

– кривая задана уравнением r = 1 + sin (t).

– кривая задана уравнением r = 1 + cos (2t).

t = 0:0.1:2*pi;

r = 1+sin(t);

polar(r,t), grid, set(gcf,'color', 'white')



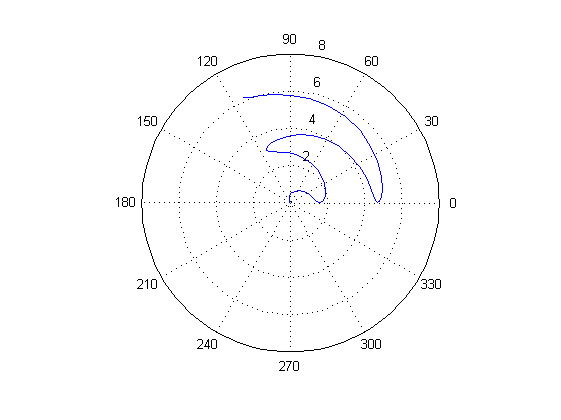
Рисунок 6: График функции r = 1 + sin (t) [0;2π]

t 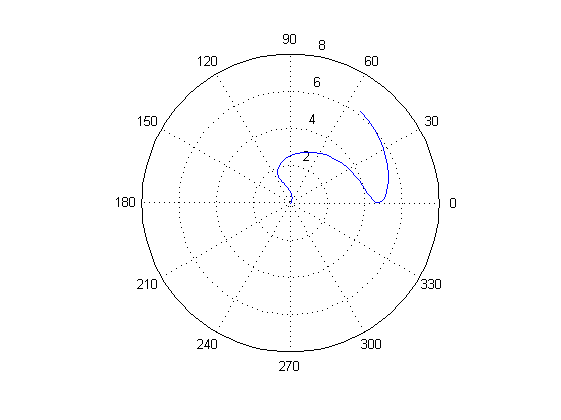= 0:0.1:2*pi;

r = 1+cos(2*t);

polar(r,t), grid, set(gcf,'color', 'white')

Рисунок 7: График функции r = 1 + cos (2t) [0;2π]

Задание 4.

Построить графики трёхмерных поверхностей. Использовать функции

---

meshgrid, plot .

– график трёхмерной поверхности, описываемый функцией

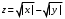
– график трёхмерной поверхности, описываемый функцией z = y2 - x2.

1) [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);

Z = sqrt(abs(X))-sqrt(abs(Y));

m esh(X, Y, Z)

Рисунок 8: График трёхмерной поверхности

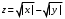
2) [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);

Z = X.^2-Y.^2;

mesh(X, Y, Z)



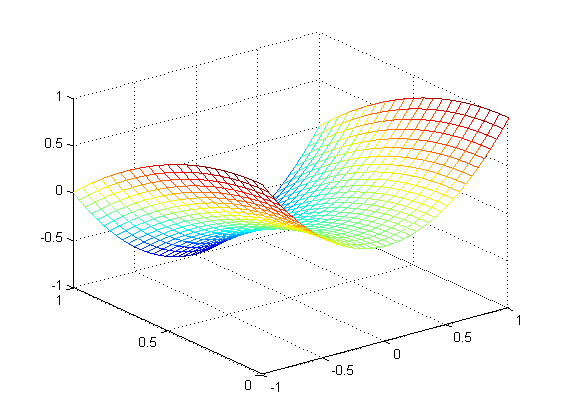
Рисунок 9: График трёхмерной поверхности z = y² - x²

Задание 5.

Построить в декартовой системе координат график вектора с комплексными элементами

у = sin x + i *cos x в диапазоне [0; 2 π], используя функцию plot.

x= 0: 0.05 : 2*pi;

>> y = sin(x) + i *cos( x )

y = plot(x,y)

Рисунок 10: График функции у = sin x + i *cos x [0;2π]

Задание 8. Постройте два графика в рамках одних осей координат:

для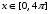

Сделайте надписи на осях, заголовок для графика, пояснительную надпись на рисунке задайте тип линий и цвет.

x=0:0.05:4*pi;

>> z = atan(x.^(1/2));

>> y=exp(-x.^2); z = atan(x.^(1/2));

>> plot(x,y,x,z),grid

>> title('Функции y = y=exp(-x^2) и z = atan(x^(1/2)) ');

>> xlabel('ось X'); ylabel('ось Y');



Рисунок 11: Графики функций y=exp(-x.^2); z = atan(x.^(1/2)) в одних осях

Задание 9. Построить графики функций y(x) и z(x) в разных подобластях одного графического окна. Интервалы изменения для х определите самостоятельно.

x1=0:0.05:2*pi;

>> z = atan(x1.^(1/2));

>> x2=0:0.05:4*pi;

>> y=exp(-x2.^2);

>> plot(x1,z,x2,y)



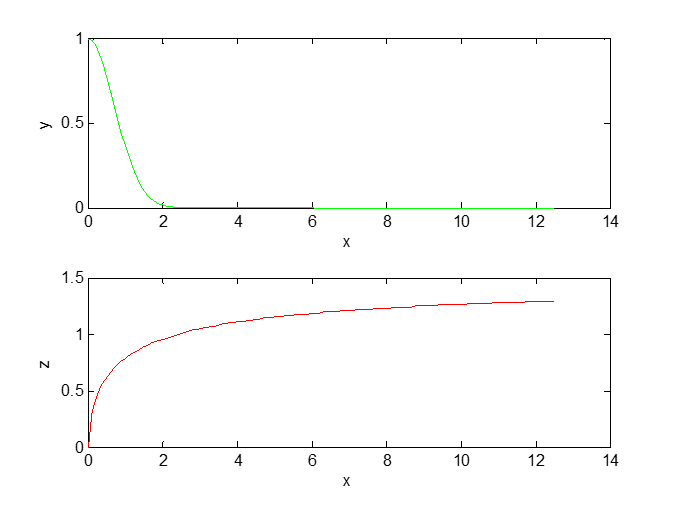
Рисунок 12: Графики функций y=exp(-x.^2); z = atan(x.^(1/2)) в разных подобластях

Задание 10. Постройте поверхность с использованием функции mesh

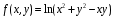, где

---

>> [x,y] = meshgrid(1:0.1:2, -5:0.1:5)

>> z = log(x.^2+y.^2-x.*y)

>> mesh(x, y, z); xlabel('x'); ylabel('y'); zlabel('z')



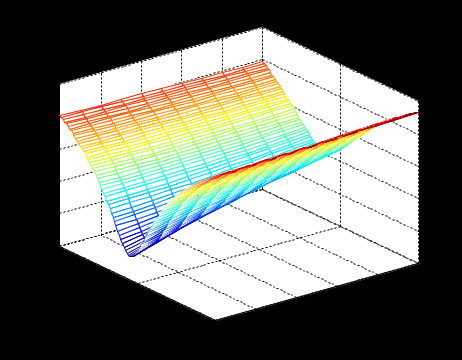
Рисунок 13: График трёхмерной поверхности z = log(x.^2+y.^2-x.*y)

Вывод: В MatLAB можно строить различные графики функций, как в декартовых, так и в полярных координатах, строить трехмерные поверхности, строить несколько графиков на одном поле и т. п. Все это реализуется с помощью специальных встроенных функций.

Лабораторная работа № 4.

Решение типовых задач алгебры и анализа

Создание процедур (файлов-функций) в среде MatLAB

Цель работы:

Целью лабораторной работы является изучение простых приемов языка программирования среды MatLAB. Основной задачей ставится изучение типовых конструкций языка, таких как функции, условия и циклы.
Задание №1

Создайте m-файл, вычисляющий значения функции f(x)на отрезке [a; b] с шагом h (Таблица 2.1). Постройте график этой функции с помощью процедуры fplotв границах, заданных в задании. Вычислите интеграл от функции в тех же пределах, используя встроенные функции. Найдите экстремумы и ближайший корень (нуль) функции.



function [ y ] = func( x )

%Вычисляет значение функции

%y=cos(pi*x^2)/sqrt(1-3*x)

y=cos(pi.*x.^2)./sqrt(1-3*x);

end

fplot(‘func’, [-1,0], 0.1, 1), grid, title(‘График функции “ y=cos(pi*x^2)/sqrt(1-3*x) “’);

>> x=-1:0.1:0;

>> y=func(x);

>> int=trapz(x,y)

int = 0.3257

>> x=-1:0.1:0;

>> y=cos(pi.*x.^2)./sqrt(1-3*x);

>> plot(x,y,'-k'),grid

>> y=func(x);

>> [xmin,ymin]=fminsearch(@func,-1)

xmin = -0.9903

ymin = -0.5009

function [ y ] = func( x )

%Вычисляет значение функции

%y=cos(pi*x^2)/sqrt(1-3*x)

y=-(cos(pi.*x.^2)./sqrt(1-3*x));

end

>> x=-1:0.1:0;

>> y=funca(x);

>> plot(x,y,'-k'),grid

>> [xmax,ymax]=fminsearch(@funca,-1)

xmax = -1.4105

ymax = -0.4370

>> x=-1:0.1:0;

>> y=cos(pi.*x.^2)./sqrt(1-3*x);

>> y=func(x);

>> plot(x,y), grid

>> x1=fzero(@func,-0.8)

x1 =-0.7071



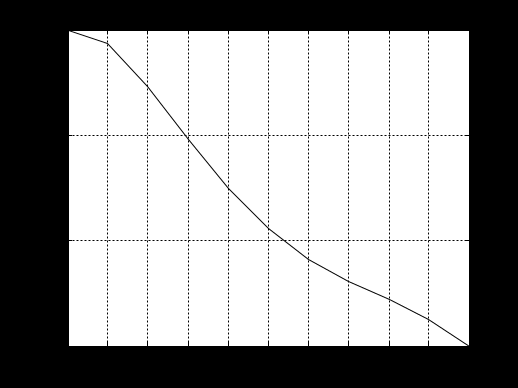
Рисунок 1: График функции y=cos(pi.*x.^2)./sqrt(1-3*x)

Рисунок 2: График функции y=cos(pi.*x.^2)./sqrt(1-3*x)

Задание №2

---

Смотрите также файлы

• Электрическое поле Близкодействие и действие на расстоянии.pptx

• Контрольная работа 2 контрольные задания.doc

• Аты Фамилия Адамда анша сезім мшелері бар.docx

• Программа среднего профессионального образования 44. 02. 03. А педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Основы философии Практическое задание 4.doc

• Описание работы Контрольная.doc