Найдите локальные экстремумы функции двух переменных, приняв за начальную, точку с заданными координатами x₀, y₀ (таблица 2.1). Предварительно создайте соответствующую файл-функцию.



>> [z,fval] = fminsearch(@(x) (exp(x(1)+x(2))+4.*x(1).^2-3.*x(1)-3.*x(2)), [0.5,1.5])

z = 0.0000 1.0986

fval = -0.2958

>> [x,y]=meshgrid(-2:0.2:2,-2:0.2:2);

>> z= exp(x+y)+4.*x.^2-3.*x-3.*y;

>> surf(x,y,z);

>> [x,fval] = fminunc(@(x) (exp(x(1)+x(2))+4.*x(1).^2-3.*x(1)-3.*x(2)), [0.5,1.5])

Warning: Gradient must be provided for trust-region algorithm;

using line-search algorithm instead.

> In fminunc at 380

Local minimum found.

Optimization completed because the size of the gradient is less than

the default value of the function tolerance.



x = 0.0000 1.0986

fval =-0.2958



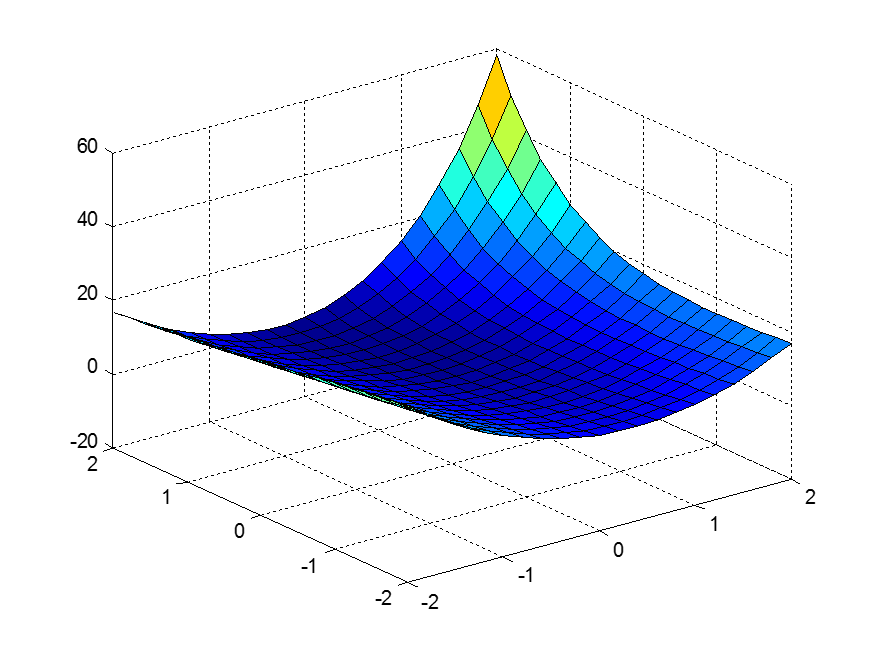
Рисунок 3: Поверхность z= exp(x+y)+4.*x.^2-3.*x-3.*y

Задание №3

Рассчитать аэродинамический нагрев тела в полете со скоростью V, в зависимости от высоты полета H для условий международной стандартной атмосферы (МСА).

Значение высоты H принять от 0 до 25000м с шагом 1000м.

Зависимость температуры атмосферы T_H[K]от высоты Н[м] определяется по формуле:

T_H= T₀ - β·Н

где β - коэффициент снижения температуры β = 6,5·10-3 [K/м];

T₀ – температура атмосферы на высоте Н = 0, T₀=288,2[K]

Начиная с высоты 11000м (тропосфера) до высоты 25000м (стратосфера) температура окружающей среды остается постоянной.

Аэродинамический нагрев ΔT*[K] рассчитывается по формуле:



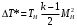
где М_Н – число Маха 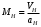_; а_Н – местная скорость звука [м/с], определяется по формуле _.

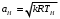Показатель адиабаты для воздуха k =1,4.

Удельная газовая постоянная R = 287,13[Дж/кг·К]

Варианты исходных данных (скорость полета V_H)

Вариант задания	4
Скорость полета [м/c]	280

1. Вывести рассчитанные данные зависимостей T_H (Н) и ΔT*(Н) в виде таблиц. Для чего после расчета сохранить их в текстовый файл.

2. Построить графики этих зависимостей.

Th(H):

H, км	0	1	2	3	4	5	6	7	8	9	10	11	12
Th, K	288.2	281.7	275.2	268.7	262.2	255.7	249.2	242.7	236.2	229.7	223.2	216.7	216.7
H, км	13	14	15	16	17	18	19	20	21	22	23	24	25
Th, K	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7	216.7

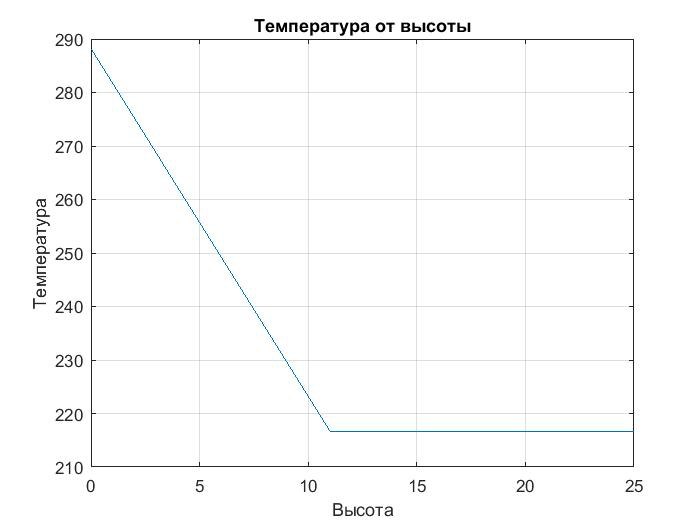
Рисунок 4: График зависимости температуры от высоты а(h):

Высота	0	1	2	3	4	5	6	7	8	9	10	11-25
а(h)	57,90439	57,24769	56,58336	55,91114	55,23074	54,54185	53,84415	53,13729	52,4209	51,69458	50,95791	50,21044

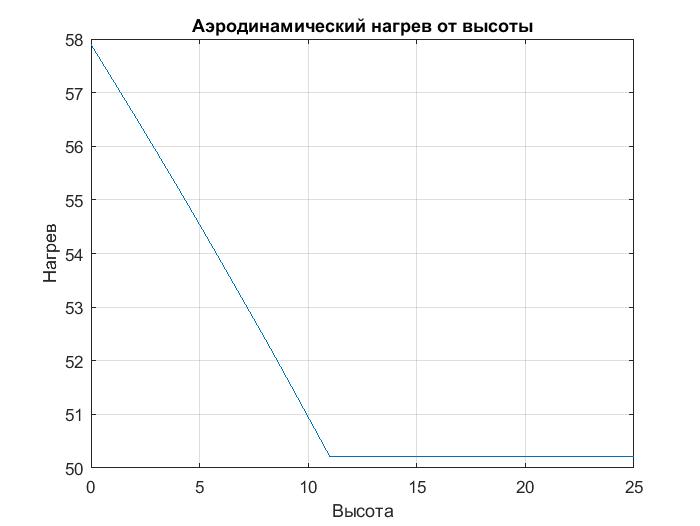
Рисунок 5: График зависимости аэродинамического нагрева от высоты

Вывод: MatLAB позволяет исследовать математические функциональные зависимости на максимумы и минимумы, экстремумы и находить точки пересечения функции с осями координат, а также решать практические задачи.

Лабораторная работа № 5.

Методы обработки экспериментальных данных

Основы работы в Curve Fitting Toolbox

Цель: 1) научиться работать с Curve Fitting Toolbox;

2) определить вид заданной функции.

Curve Fitting Toolbox позволяет:

1. Работать с данными, заданными при помощи векторов в рабочей среде MATLAB, и, при необходимости, снабжать данные весами, так же задавая вектор их значений.

2. Графически отображать исследуемые данные.

3. Осуществлять предварительную обработку данных, исключая часть данных по некоторому правилу, по точкам в таблице, или при помощи мыши на графике, или наоборот оставляя часть данных для последующей обработки.

4. Сглаживать и фильтровать данные различными способами.

5. Приближать данные при помощи параметрических моделей, в которых искомые параметры могут входить как линейно, так и нелинейно. Модели выбираются из библиотеки моделей, или задаются пользователем. Целевая функция ошибки и методы, применяемые для ее минимизации, так же могут быть различными. Допускается задание ограничений на искомые значения параметров. Кроме параметрических моделей, возможна интерполяция данных сплайнами и приближение сглаживающими сплайнами.

6. Отображать построенные приближения графически, форматировать графики и сохранять результаты в отдельных графических окнах.

7. Вычислять различные критерии пригодности полученного приближения.

8. Производить ряд операций с полученными приближениями (вычислять в заданных точках, дифференцировать интегрировать, проводить экстраполяцию), графически отображать результат.

П 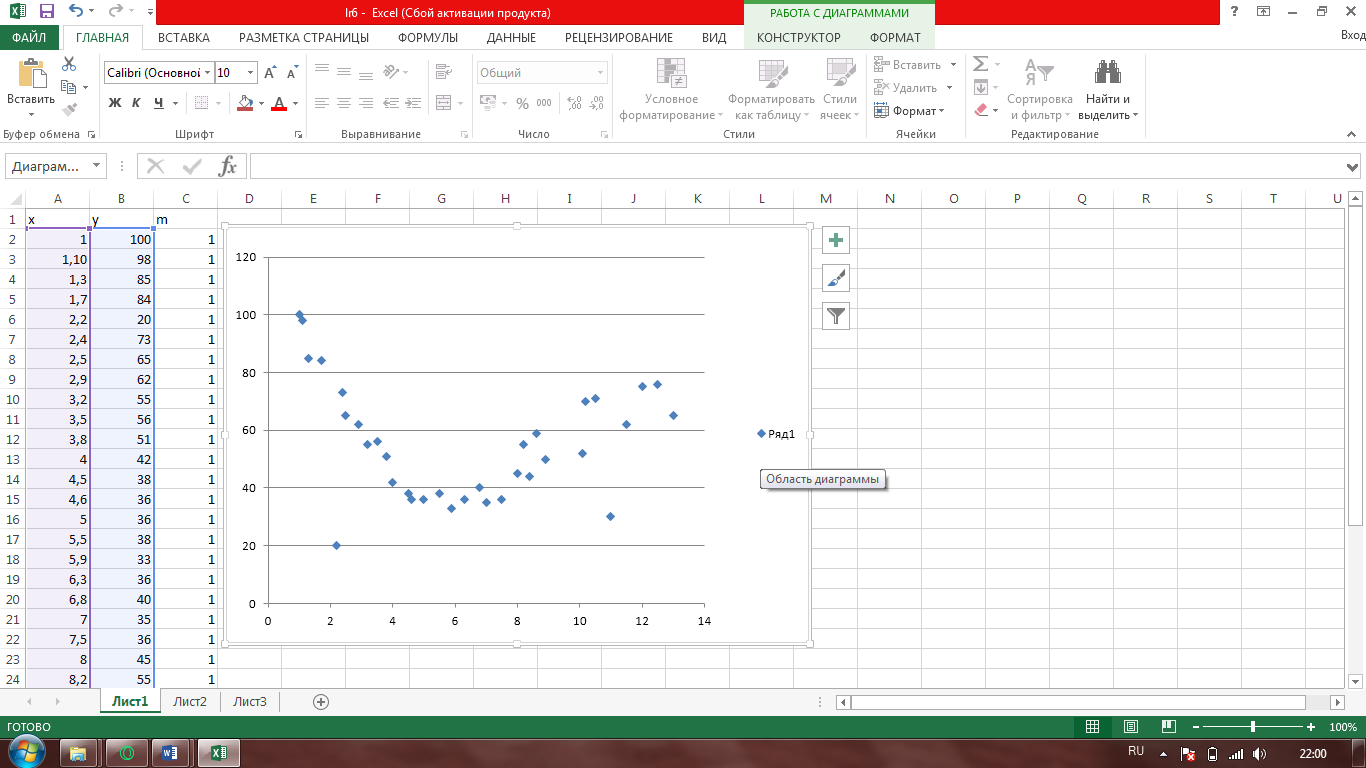риблизительно были определены точки по графику неизвестной функции, построена точечная диаграмма в программе MS Excel:

Рис. 1. Примерный вид графика

Импортируем данные о значениях координатах и массах точек.

Построенной точечной диаграмме сопоставляем предложенные программой виды различных функций.

Находим функцию, которая имеет минимальные ошибки.



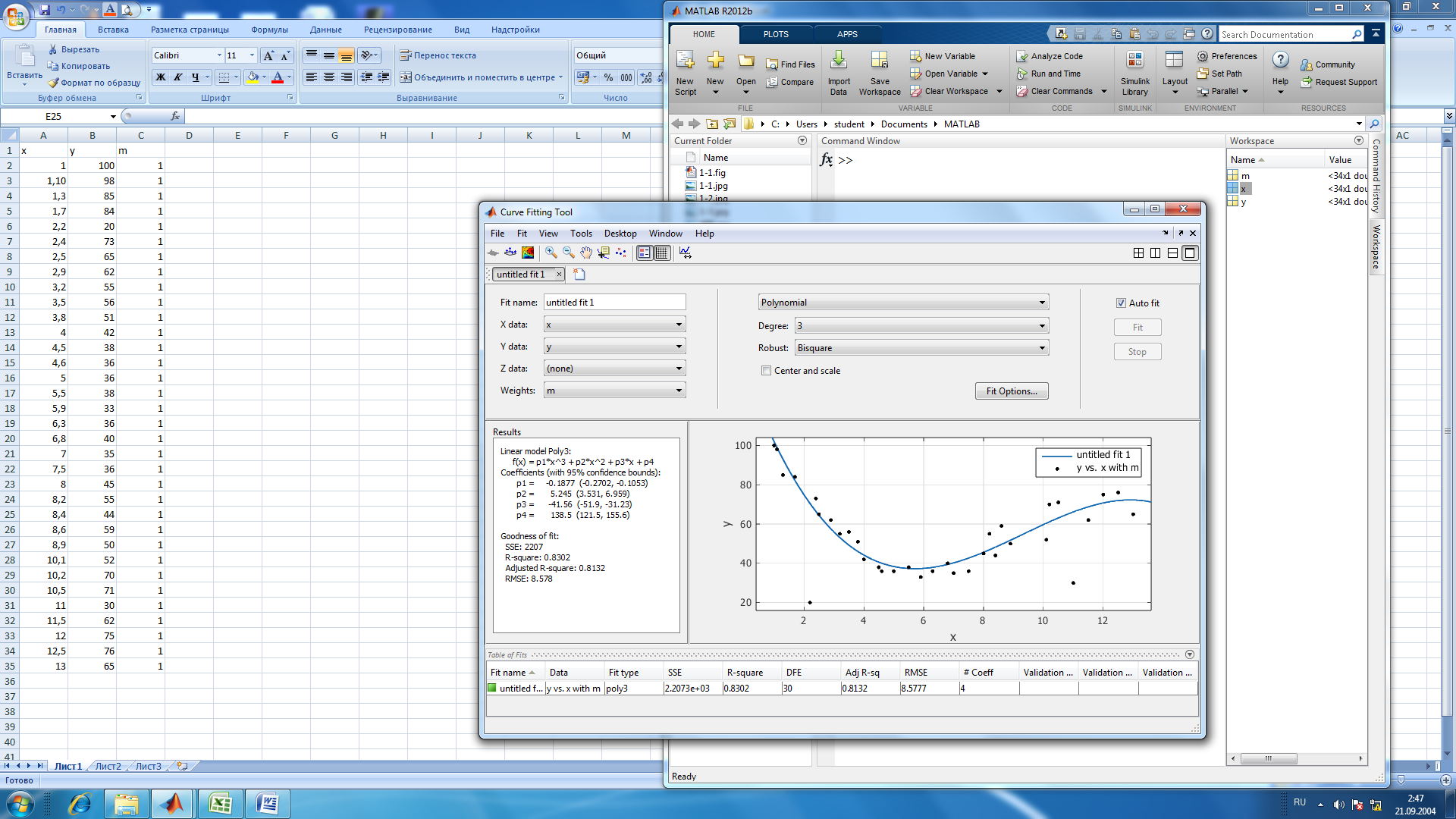
Рис.2. Результаты приближения данных полиномом третьей степени

Linear model Poly3:

f(x) = p1*x^3 + p2*x^2 + p3*x + p4

Coefficients (with 95% confidence bounds):

p1 = -0.1877 (-0.2702, -0.1053)

p2 = 5.245 (3.531, 6.959)

p3 = -41.56 (-51.9, -31.23)

p4 = 138.5 (121.5, 155.6)

Goodness of fit:

SSE: 2207

R-square: 0.8302

Adjusted R-square: 0.8132

RMSE: 8.578



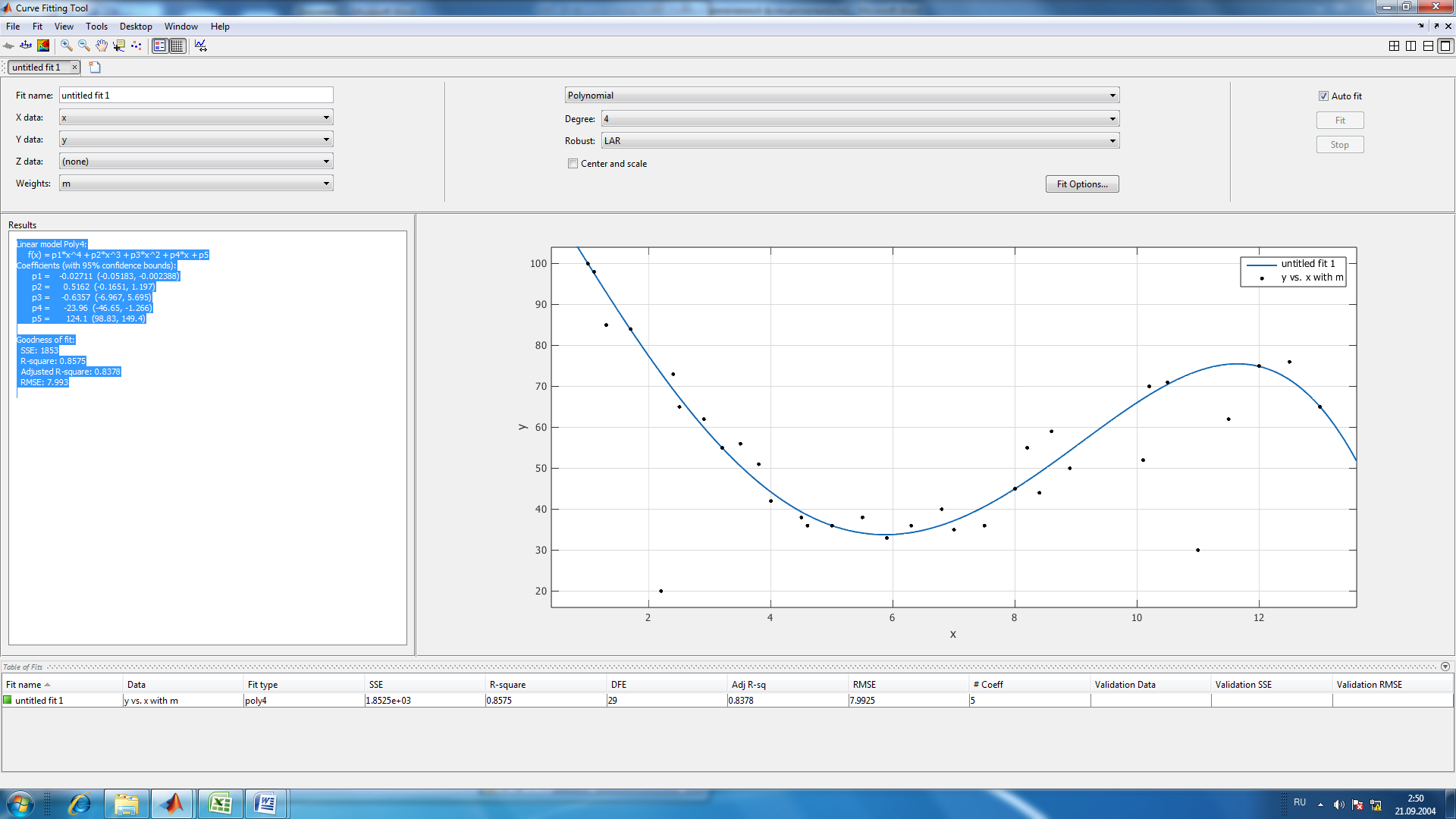
Рис.3. Результаты приближения данных полиномом четвертой степени

Linear model Poly4:

f(x) = p1*x^4 + p2*x^3 + p3*x^2 + p4*x + p5

Coefficients (with 95% confidence bounds):

p1 = -0.02711 (-0.05183, -0.002388)

p2 = 0.5162 (-0.1651, 1.197)

p3 = -0.6357 (-6.967, 5.695)

p4 = -23.96 (-46.65, -1.266)

p5 = 124.1 (98.83, 149.4)

Goodness of fit:

SSE: 1853

R-square: 0.8575

Adjusted R-square: 0.8378

RMSE: 7.993



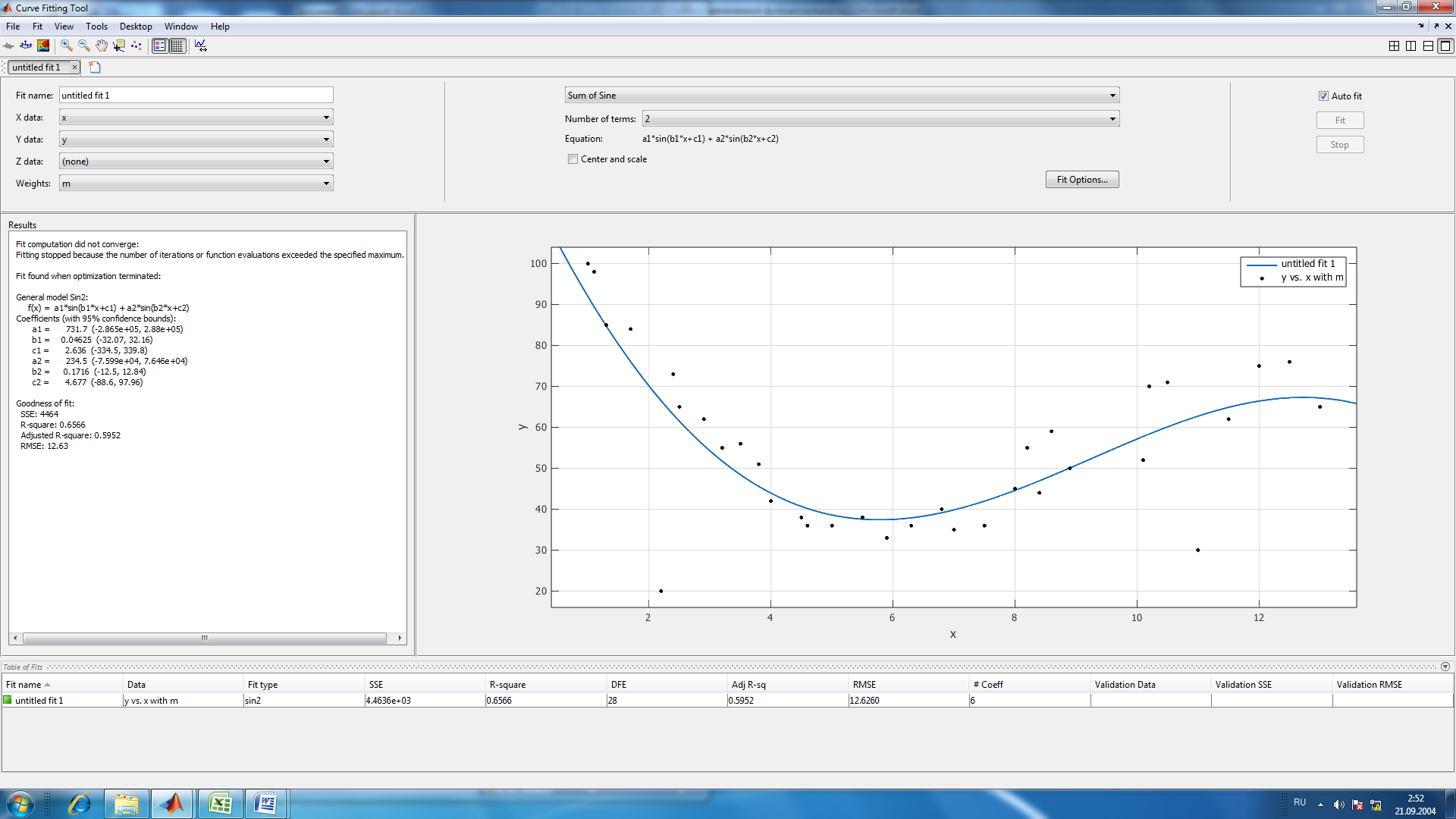
Рис.4. Результаты приближения данных функцией суммы синусов

Fit computation did not converge: Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum. Fit found when optimization terminated:

General model Sin2:

f(x) = a1*sin(b1*x+c1) + a2*sin(b2*x+c2)

Coefficients (with 95% confidence bounds):

a1 = 731.7 (-2.865e+05, 2.88e+05)

b1 = 0.04625 (-32.07, 32.16)

c1 = 2.636 (-334.5, 339.8)

a2 = 234.5 (-7.599e+04, 7.646e+04)

b2 = 0.1716 (-12.5, 12.84)

c2 = 4.677 (-88.6, 97.96)

Goodness of fit:

SSE: 4464

R-square: 0.6566

Adjusted R-square: 0.5952

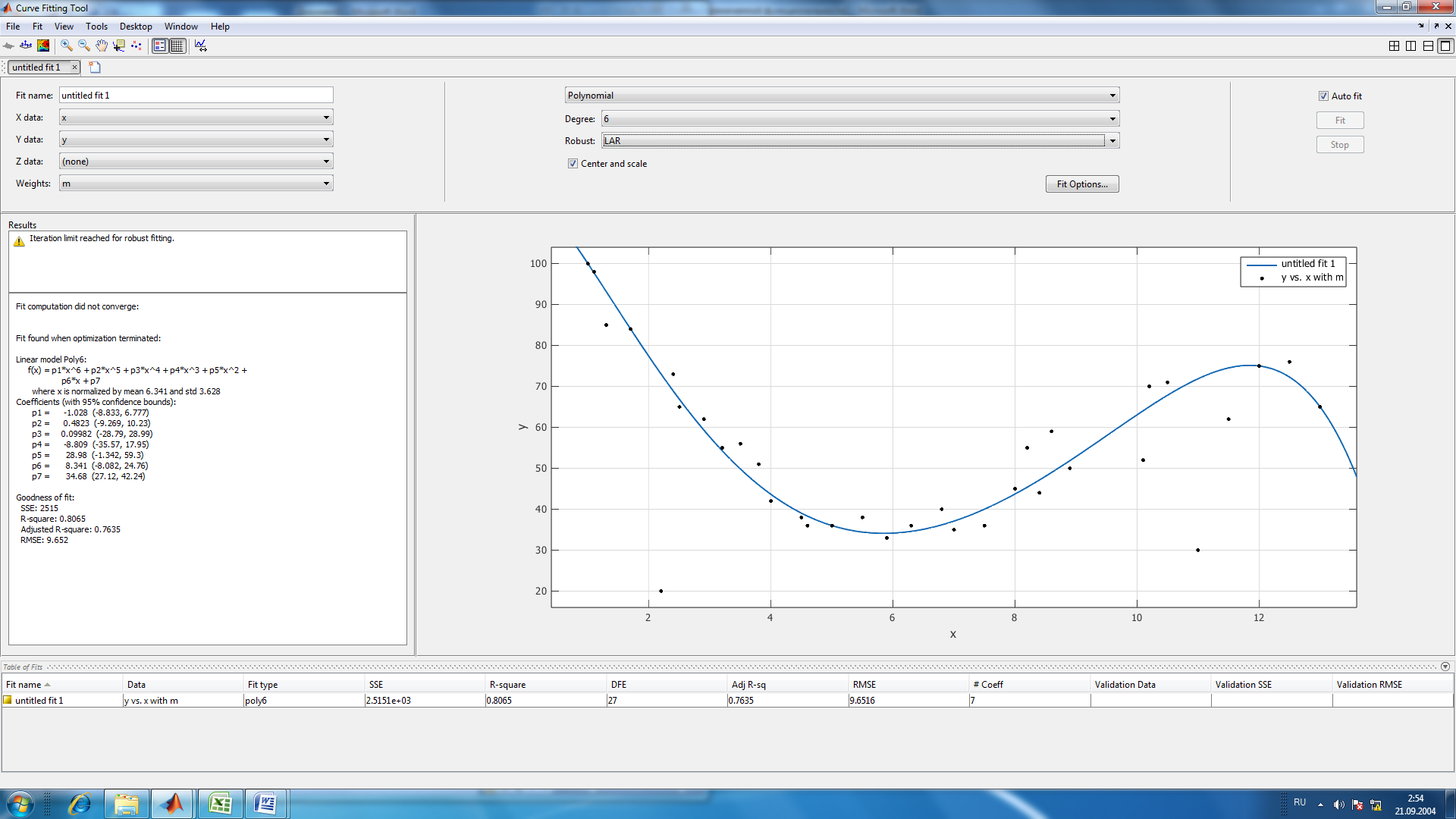
RMSE: 12.63

Рис.5. Результаты приближения данных полиномом шестой степени

Fit computation did not converge: Fit found when optimization terminated:

Linear model Poly6:

f(x) = p1*x^6 + p2*x^5 + p3*x^4 + p4*x^3 + p5*x^2 + p6*x + p7

where x is normalized by mean 6.341 and std 3.628

Coefficients (with 95% confidence bounds):

p1 = -1.028 (-8.833, 6.777)

p2 = 0.4823 (-9.269, 10.23)

p3 = 0.09982 (-28.79, 28.99)

p4 = -8.809 (-35.57, 17.95)

p5 = 28.98 (-1.342, 59.3)

p6 = 8.341 (-8.082, 24.76)

p7 = 34.68 (27.12, 42.24)

Goodness of fit:

SSE: 2515

R-square: 0.8065

Adjusted R-square: 0.7635

RMSE: 9.652

Вывод:

1) В Matlab с помощью средств Curve, Fitting и Toolbox можно определять вид любой неизвестной функции, коэффициенты уравнения, которыми она задана, рассчитать погрешность, с которой построена эта функция относительно приближенных значений.

2) Минимальные значения ошибок достигаются при приближении полиномом четвертой степени. Значение SSE должно стремиться к нулю, но, в связи с большими значениями функции по Х и по У, SSE увеличился.

Контрольное задание

1. 
   Разработать алгоритм в виде блок-схемы. Оформить программы поиска корней уравнений из табл. 1.2. по вариантам методом сканирования и уточнения значения корней методом хорд и методом половинного деления.
   

Сравнить количество итераций при решении уравнений методами половинного деления и хорд с заданной точностью вычислений.

Код:

xn=1;

xk=4;

% c=0;

% x0=0;

step_x=0.01;

x=xn:step_x:xk;

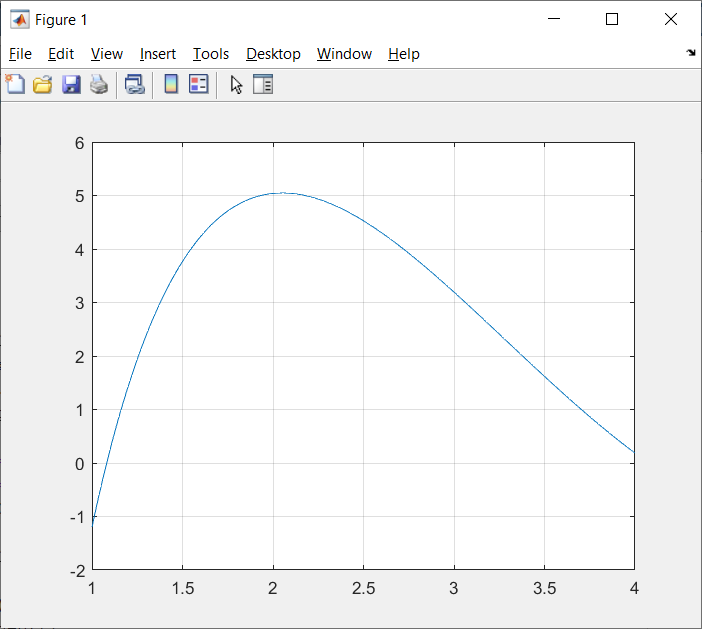
y=(x-5).^2.*log(x)-1.2;

plot(x,y),grid;

disp("");

a=input("a= ");

b=input("b= ");

epsilon=0.0001; %input("погрешность e1= ");

for i=1:15

epsilon=0.1^i;

n=0;

while((b-a)>epsilon)

c=(a+b)/2;

ya=kontrF(a);

yb=kontrF(b);

yc=kontrF(c);

if(ya*yc<0)

b=c;

else

a=c;

end

n=n+1;

end

disp(fprintf('Корень, вычисленный методом половинных отрезков = %.15f за %d итераций',c,n));

input("Правая граница a= ");

input("Левая граница b= ");

n2=0;

while((b-a)>epsilon)

ya=kontrF(a);

yb=kontrF(b);

c=(a*abs(yb)+abs(ya)*b)/(abs(yb)+abs(ya));

yc=kontrF(c);

if(ya*yc<0)

b=c;

else

a=c;

end

n2=n2+1;

end

end

disp(fprintf('Корень, вычисленный методом хорд = %.15f за %d итераций',c,n2));

Функция kontrF:
function [y] = code(x)
y=(x-5)^2*log(x)-1.2;
end







Да

Да

Нет

Нет

b=c

a=c

n=n+1

y_a*y_c < 0

Конец

c = (a+b)/2

y_a=kontrF(a)

y_b=kontrF(b)

y_c=kontrF(c)

Начало

|b-a|>E

a, b, f(x), E



Вывод корня и числа итераций


Вывод:

1) С помощью MatLab был создан алгоритм поиска корней методом хорд и методом половинного деления.

---

Смотрите также файлы

• Электрическое поле Близкодействие и действие на расстоянии.pptx

• Контрольная работа 2 контрольные задания.doc

• Аты Фамилия Адамда анша сезім мшелері бар.docx

• Программа среднего профессионального образования 44. 02. 03. А педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Основы философии Практическое задание 4.doc

• Описание работы Контрольная.doc