Программа среднего профессионального образования

44.02.02 Преподавание в начальных классах

Дисциплина: Математика.

Практическое занятие 6


Выполнил:

Обучающийся Тимошина Светлана Сергеевна

Преподаватель:

Галкина Людмила Сергеевна


Задание 1. (Максимальное количество баллов – 1 балл)

Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):






Ответ: х=-5

Задание 2. (Максимальное количество баллов – 1 балл)

Р
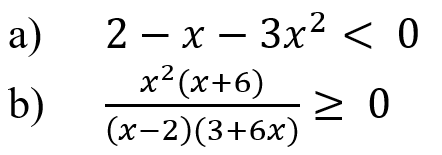
ешите предложенные неравенства методом интервалов, подробно описывая ход решения:






З
адание b)





Задание 3. (Максимальное количество баллов – 2 балла)

Найдите значение выражений, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

---

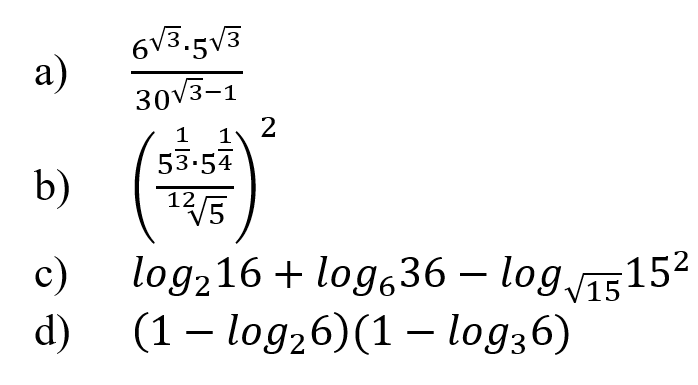
Задание с:





Задание d:










Задание 4. (Максимальное количество баллов – 2 балла)

Решите предложенные уравнения, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты):

Задание а)










Задание b)











Задание с:











Задание d:








Задание 5. (Максимальное количество баллов – 2 балла)

Решите предложенные неравенства

---

, подробно описывая ход решения (указывайте формулы и положения, которыми пользуетесь, записывайте промежуточные результаты):





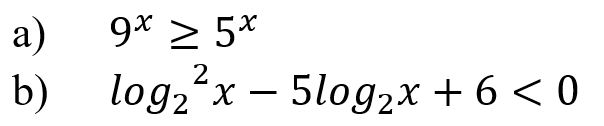
Задание а)



Задание b)





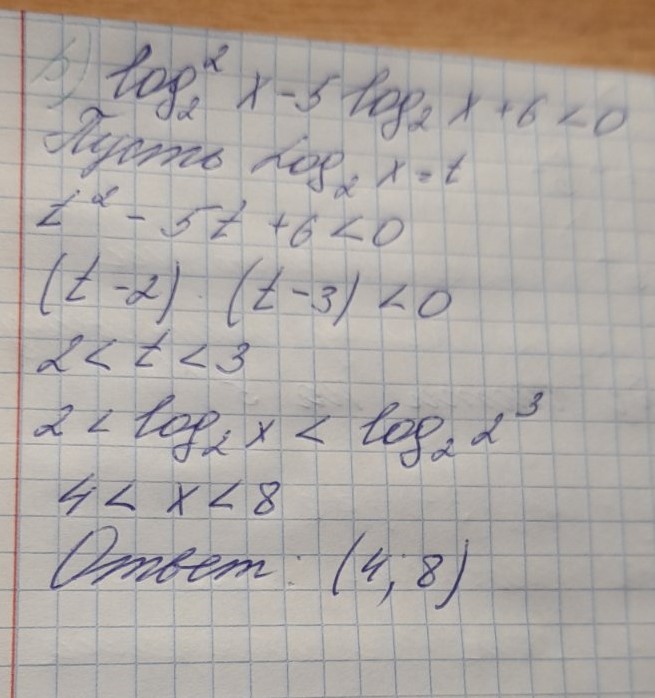
Задание 6. (Максимальное количество баллов – 3 балла)

Решите предложенные тригонометрические уравнения и неравенства, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, отобразите графически на единичной окружности соответствующие точки и интервалы):





Задание а)





Задание b)





Задание 8. (Максимальное количество баллов - 4 балла)

В
ам предложена функция

Проведите исследование, согласно схеме:

1.Найти область определения функции.

2.Найти точки пересечения с осями.

3.Исследовать функцию на четность/нечетность.

4.Найти асимптоты.

5.Найти экстремумы и интервалы монотонности функции.

6.Найти интервалы выпуклости функции и точки перегиба.

7.Найти дополнительные точки, уточняющие график.

8.Построить график.

1) Область определения функции. Точки разрыва функции.

D(y)=R, но х≠±2

2) Четность или нечетность функции.

y(-x) = y(x), четная функция

3) Периодичность функции.

4) Точки пересечения кривой с осями координат.

Пересечение с осью 0Y

x=0, y=0

Пересечение с осью 0X

y=0

x₁=0

5) Исследование на экстремум.

y = x^2/(x^2-4)

Найдем точки разрыва функции.

x₁ = 2

x₂ = -2

Поскольку f(-x)=f(x), то функция является четной.

1. Находим интервалы возрастания и убывания. Первая производная.

---

или

Находим нули функции. Для этого приравниваем производную к нулю

x = 0

Откуда:

x₁ = 0

(-∞ ;-2)	(-2; 0)	(0; 2)	(2; +∞)
f '(x) > 0	f '(x) > 0	f '(x) < 0	f '(x) < 0
функция возрастает	функция возрастает	функция убывает	функция убывает

В окрестности точки x = 0 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0 - точка максимума.

2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.

или

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Для данного уравнения корней нет.

(-∞ ;-2)	(-2; 2)	(2; +∞)
f ''(x) > 0	f ''(x) < 0	f ''(x) > 0
функция вогнута	функция выпукла	функция вогнута

6) Асимптоты кривой.

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

Находим коэффициент b:

Получаем уравнение горизонтальной асимптоты:

y = 1

Найдем вертикальные асимптоты. Для этого определим точки разрыва:

x₁ = -2

x₂ = 2

Находим переделы в точке x=-2

x₁ = -2 - точка разрыва II рода и является вертикальной асимптотой.

Находим переделы в точке x=2

x₂ = 2 - точка разрыва II рода и является вертикальной асимптотой.

Найдем наклонную асимптоту при x → -∞:

Находим коэффициент k:

Находим коэффициент b:

Получаем уравнение горизонтальной асимптоты:

y = 1





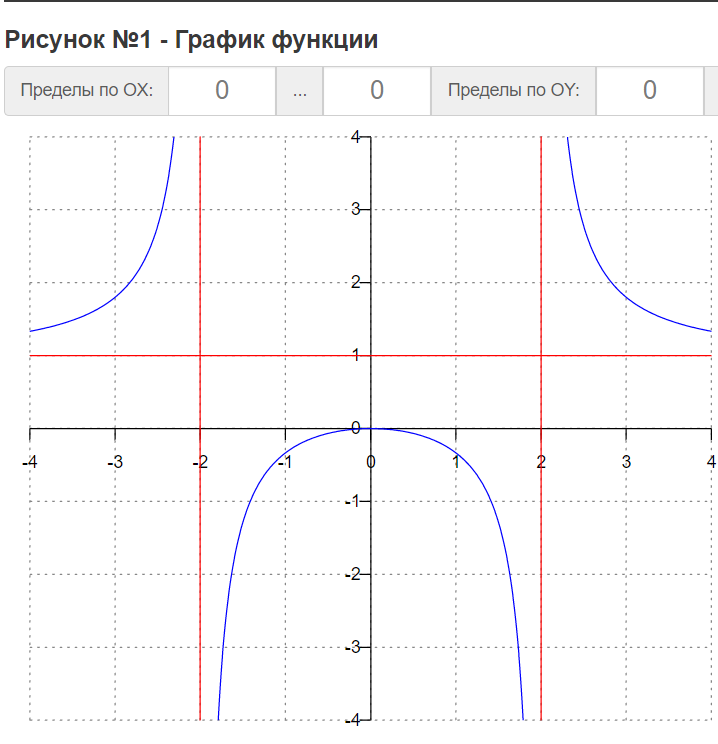
Задание 9. (Максимальное количество баллов – 2 балл)

Вычислите предложенные неопределенные интегралы, подробно описывая ход решения (указывайте формулы, которыми пользуетесь, записывайте промежуточные результаты).

---

Задание а)





Задание b)





Задание 12. (Максимальное количество баллов – 3 балла)

Изучите предложенные исходные данные, полученные при измерении:

Номер измерения	1	2	3	4	5	6	7	8	9	10
Данные	1	1	2	2	4	4	4	5	5	5

Выполните задания с учетом исходных данных, подробно описывая ход вашего решения:

a)  Построить полигон распределения.

b)  Вычислить выборочную среднюю, дисперсию, моду, медиану.

c)   Найти коэффициент вариации и сделать выводы

Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.

Таблица для расчета показателей.

xi	Кол-во, fi	xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi	Относительная частота, fi/f
1	2	2	2	4.6	10.58	0.2
2	2	4	4	2.6	3.38	0.2
4	3	12	7	2.1	1.47	0.3
5	3	15	10	5.1	8.67	0.3
Итого	10	33		14.4	24.1	1

---

Смотрите также файлы

• Пермский национальный исследовательский политехнический университет Аэрокосмический факультет кафедра Авиационные двигатели.docx

• Электрическое поле Близкодействие и действие на расстоянии.pptx

• Контрольная работа 2 контрольные задания.doc

• Аты Фамилия Адамда анша сезім мшелері бар.docx

• Программа среднего профессионального образования 44. 02. 03. А педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Основы философии Практическое задание 4.doc