ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 203
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вынесение на местность точки с проектной отметкой
Перенесение на местность проектной отметки.
Исходные данные:
- точка высотное положение которой известно (репер, марка);
- точка на которую нужно предносить проектную отметку;
- нивелир или теодолит;
Схема перенесения на местность проектной отметки
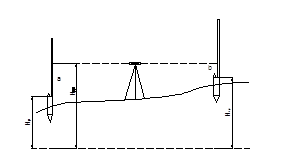
1.Установить нивелир между репером и колом, на который передают отметку.
2.Взять отсчёт по чёрной стороне рейки установленной на репере a и вычислить высоту горизонта прибора
3.Вычислить отсчёт, который должен быть прочитан по рейке установленной на колышке, чтобы отметка его верхнего среза равнялась Нпр
4. Забивают кол в землю добиваясь равенства прочитанного и вычисленного отсчётов (вытаскивать колышки до проектной отметки не разрешается)
5.Контроль переноса проводят повторным измерением с изменением высоты установки прибора ( )
Пробные отсчеты по рейкам
Δh1= a1-b1 Δhлист=a1-b1
Δh2=a2-b2
“Из середины”
a1черн. зад=
a2 кр. зад=
b1черн. перед=
b2 кр. Перед=
Δh черн.=
Δh кр.=
Δh ср.=
“Из вне”
a1черн. зад=
a2 кр. зад=
b1черн. перед=
b2 кр. перед=
Δh черн.=
Δh кр.=
Δh ср.=
Дата_____________
Погодные условия: ____________________
Журнал измерения углов теодолитного хода
ПРИМЕР
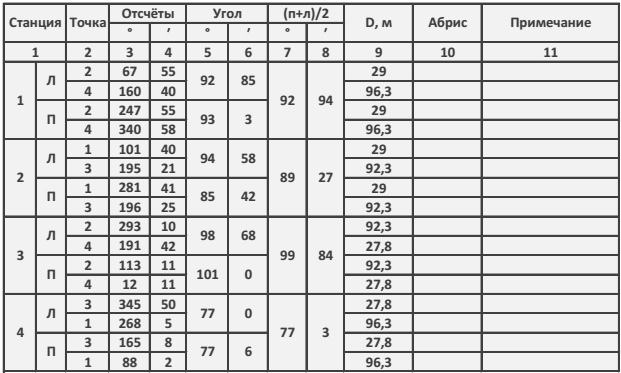
Расписать все вычисления
Дата: __________________
Погодные условия: ____________________
Журнал измерения высот теодолитного хода
ПРИМЕР
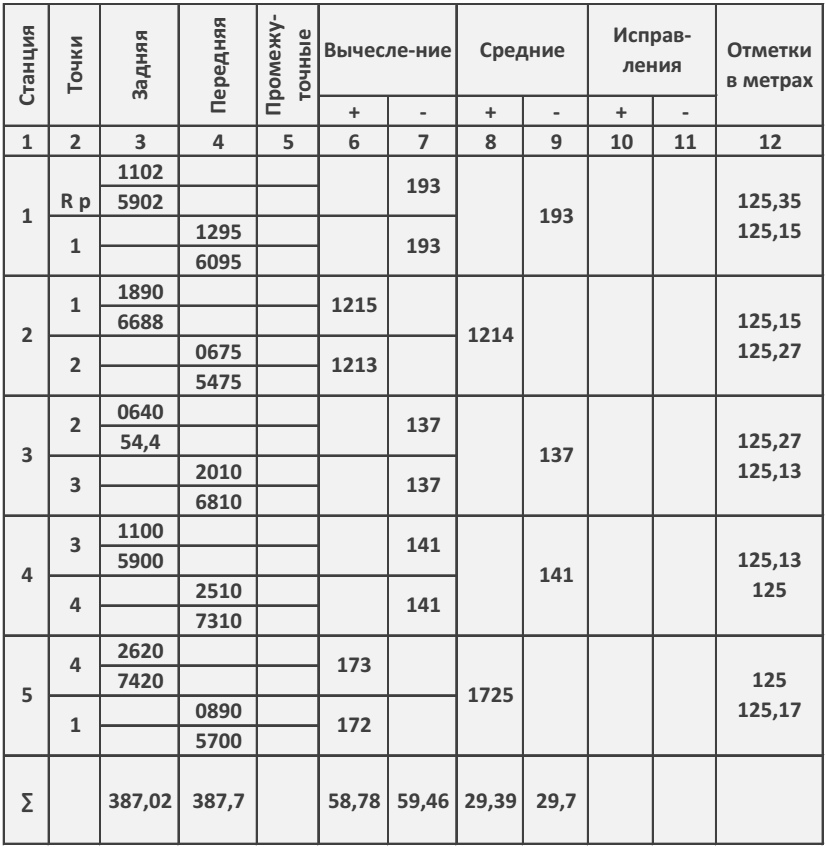
Все вычисления записать после таблицы
Дата: ______________
Погодные условия: ___________________
ПРИМЕР
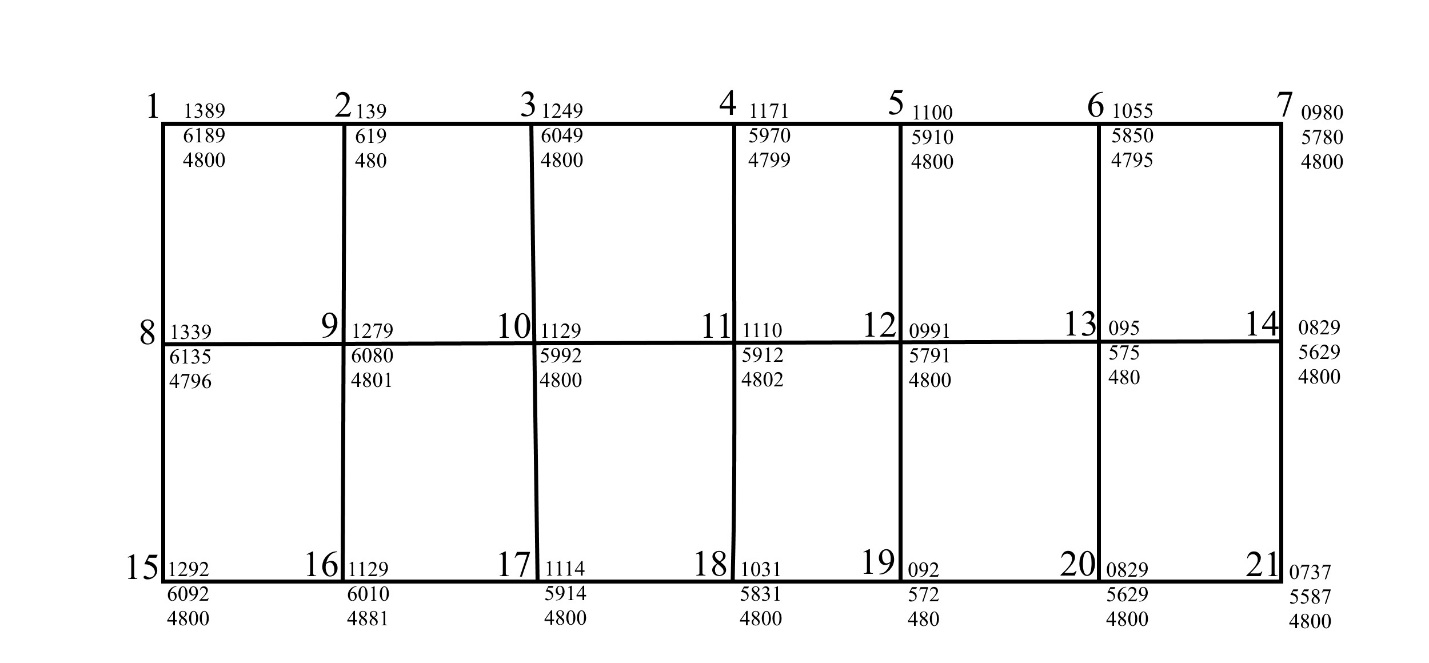
Расписать все вычисления
Hru=Hrp+a=
H1=Hru-b1=
H2=
H3=
H4=
H1=
H2=
H3=
H4=
H5=
H6=
H7=
H8=
H9=
H10=
H11=
H12=
H13=
H14=
H15=
H16=
H17=
H18=
H19=
H20=
H21=
Решение прямой и обратной геодезической задачи
Прямая геодезическая задача

Прямая геодезическая задача
Дано: координаты точки 1 х1, у1; горизонтальное проложение линии 1 – 2: d1,2;
дирекционный угол линии 1 – 2: a1,2 (рис.3.5).
Найти: координаты точки 2: х2, у2.
Решение: координаты точки 2: х2 = х1 + Dх; у2 = у1 + Dу,
где приращения координат Dх = d · cos a; Dу = d · sin a,
откуда х2 = х1 + d · cos a; у2 = у1 + d · sin a.
Знаки приращений координат Dх и Dу зависят от знаков функций sin a и cos a.
б) Обратная геодезическая задача
| | |
| |  |
Обратная геодезическая задача
Дано: координаты точек 1 и 2: х1, у1; х2, у2 (рис.3.6).
Найти: горизонтальное проложение линии 1 – 2: d1,2; дирекционный угол линии 1 – 2: a1,2.
Решение: Dх = х2 – х1; Dу = у2 – у1;
По значению tg a определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
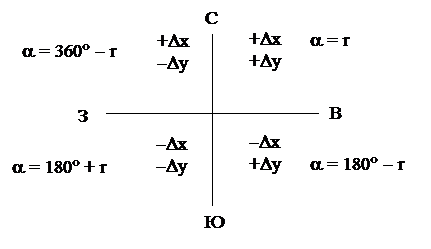
Знаки приращений координат
в зависимости от четверти
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.
Ориентировать – значит найти направление заданной линии относительно другого направления, принятого за исходное.
За исходное направление в геодезии принимают:
а) Астрономический (истинный меридиан)
| | |
| |  |
Истинный азимут
А – астрономический (истинный) азимутлинии – горизонтальный угол, отсчитываемый в данной точке от северного конца истинного меридиана по ходу часовой стрелки до направления ориентируемой линии .
А – прямой истинный азимут, Аобр – обратный.
б) Магнитный меридиан

.Магнитный азимут
Ам – магнитный азимут линии – горизонтальный угол, отсчитываемый в данной точке от северного конца магнитного меридиана по ходу часовой стрелки до направления ориентируемой линии,
А – истинный азимут,
d – склонение магнитной стрелки – угол между истинным и магнитным меридианами.
d со знаком «+» при положении магнитного меридиана вправо от истинного меридиана, и со знаком «–» при положении влево.
Ам = А – d
Пример 1:
Ам = 308°33¢, d = - 6° 27¢. Найти А.
А = Ам + d = 308°33¢ - 6° 27¢ = 302°06¢.
| | |
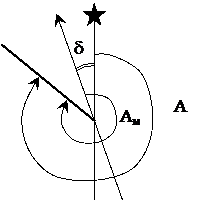 | |
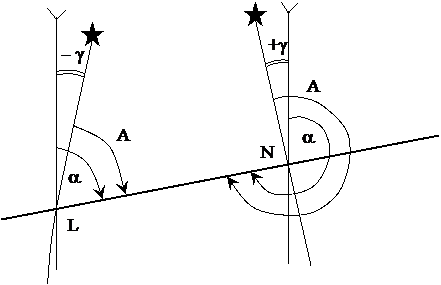 в) Осевой меридиан зоны
в) Осевой меридиан зоныДирекционный угол
a – дирекционный угол линии – горизонтальный угол, отсчитываемый в данной точке от северного конца осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до направления ориентируемой линии (рис.3.3).
a – дирекционный угол линии LN, aобр – дирекционный угол линии NL.
Связь прямого и обратного дирекционных углов можно выразить уравнением:
aобр = a ± 180°.
Связь истинного азимута и дирекционного угла выражается формулой
А = a + g,
где g – сближение меридианов – угол между истинным и осевым меридианами.
g имеет знак «+», если осевой меридиан расположен вправо от истинного меридиана, и знак «–»,если осевой меридиан расположен влево от истинного меридиана.
Пример 2: g = -2° 35¢, a = 168° 47¢. Вычислить А.
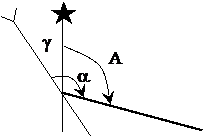 А = a + g = 168° 47¢ + (-2° 35¢) = 166° 12¢.
А = a + g = 168° 47¢ + (-2° 35¢) = 166° 12¢.Пример 3: g = + 4° 11¢, А = 312° 56¢. Вычислить a.
 А = a + g; a = А -g = 312° 56¢ - 4° 11¢ = 308° 45¢.
А = a + g; a = А -g = 312° 56¢ - 4° 11¢ = 308° 45¢.г) Румбы
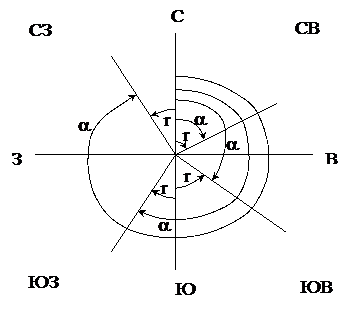
Иногда вместо дирекционных углов используют румбы. Румб – острый угол, отсчитываемый от ближайшего (северного или южного) конца осевого меридиана до направления определяемой линии (рис.3.4).
Связь между дирекционными углами и румбами:
СВ: r = a;
ЮВ: r = 180° - a, a = 180° - r;
ЮЗ: r = a - 180°, a = 180° + r;
СЗ: r = 360° - a, a = 360° - r.
| | |
| |  |
|
А = a + g;
Ам = А – d;
Ам = a + g – d.
Пример 4:
r = ЮЗ: 56°41¢, a = 180° + 56°41¢ = 236°41¢.
| | |
| | 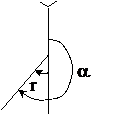 |
Пример 5:
a = 92°11¢, g = - 4° 30¢, d = - 9° 42¢. Найти А и Ам.
А = 92°11¢ - 4° 30¢ = 87°41¢,
Ам = 87°41¢ + 9° 42¢ = 97°23¢.
| | |
| | 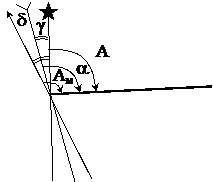 |
Фотоотчет
Схема теодолитного хода

1
3
2