Билет №1
-
Дайте определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Запишите формулу сумму углов выпуклого многоугольника.
-
Д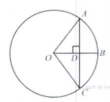 окажите теорему о средней линии треугольника. окажите теорему о средней линии треугольника.
-
Радиус ОВ окружности с центром в точке О пересекает хорду АС в точкеD и перпендикулярен ей. Найдите длину хорды АС, если BD = 1 см, а радиус окружности равен 5 см.
-
Периметр прямоугольника равен 56, а диагональ равна 20. Найдите площадь этого прямоугольника.
|
Б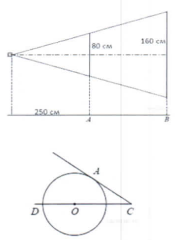 илет №2 илет №2
-
Дайте определение и свойства параллелограмма.
-
Докажите свойство медиан треугольника.
-
Проектор полностью освещает экран А высотой 80 см, расположенный на расстоянии 25 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран В высотой 160 см, чтобы он полностью был освещен, если настройки проектора остаются неизменными?
-
Найдите угол АСО, если его сторона СА касается окружности, О – центр окружности, а дуга АD окружности, заключенная внутри этого угла, равна 100о.
|
Билет №3
-
Дайте определение и назовите свойства прямоугольника.
-
Докажите теорему Пифагора.
-
Н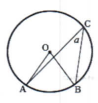 айдите величину (в градусах) вписанного угла α, опирающегося на хорду АВ, равную радиусу окружности. айдите величину (в градусах) вписанного угла α, опирающегося на хорду АВ, равную радиусу окружности.
-
Прямая, параллельная основаниям MP и NK трапеции MNPK, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны MP и NK в точках А и В соответственно. Найдите длину отрезка АВ, если MP = 40 см, NK = 24 см.
|
Билет №4
-
Дайте определение и назовите свойства ромба.
-
Докажите теорему о вписанном угле (любой частный случай).
-
Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их соответственно равны 15 км/ч и 20 км/ч. Какое расстояние (в километрах) будет между ними через два часа?
-
В треугольнике АВС углы А и С равны 20 и 60 соответственно. Найдите угол между высотой ВН и биссектрисой BD.
|
Билет №5
-
Дайте определение трапеции. Назовите виды трапеций.
-
Д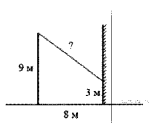 окажите свойство отрезков касательных, проведенных к окружности из одной точки. окажите свойство отрезков касательных, проведенных к окружности из одной точки.
-
От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли. Расстояние от дома до столба 8 м. Вычислите длину провода.
-
Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 16, DC = 24, АС = 25.
|
Билет №6
-
Дайте определение подобных треугольников. Назовите признаки подобия треугольников.
-
Д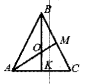 окажите признак параллелограмма (по точке пересечения диагоналей). окажите признак параллелограмма (по точке пересечения диагоналей).
-
В равностороннем треугольнике АВС медианы ВК и АМ пересекаются в точке О. Найдите ∠АОК.
-
Окружность с центром на стороне АС треугольника АВС проходит через вершину С и касается прямой АВ в точке В. Найдите АС, если диаметр окружности равен 7,5, а АВ = 2.
|
Билет №7
-
Д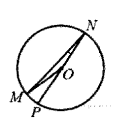 айте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. айте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
-
Докажите свойство диагоналей параллелограмма.
-
Найдите градусную меру ∠MON, если известно, NP – диаметр, а градусная мера ∠MNPравна 18о.
-
В треугольнике АВС отмечены середины M и N сторон ВС и АС соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырехугольника ABMN.
|
Билет №8
-
Назовите значение синуса, косинуса и тангенса углов 30о, 45о, 60о.
-
Д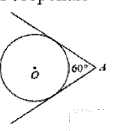 окажите свойства противоположных сторон и углов параллелограмма. окажите свойства противоположных сторон и углов параллелограмма.
-
У треугольника со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведенная к первой стороне равна 1. Чему равна высота, проведенная ко второй стороне?
-
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60о, а расстояние от точки А до точки о равно 8.
|
Билет №9
-
Д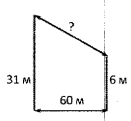 айте определение секущей и касательной к окружности. айте определение секущей и касательной к окружности.
-
Докажите свойство диагоналей прямоугольника.
-
В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой – 6 м. Найдите расстояние (в метрах) между их верхушками
-
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АК = 18, а сторона АС в 1,2 раза больше стороны ВС.
|
Билет №10
-
Дайте определение вписанного и центрального углов окружности.
-
Д окажите признак параллелограмма по двум противоположным сторонам, которые равны и параллельны. окажите признак параллелограмма по двум противоположным сторонам, которые равны и параллельны.
-
Человек ростом 1,7 м стоит на расстоянии 8 шагов от столба, на котором висит фонарь. Тень человека равна четырем шагам. На какой высоте (в метрах) расположен фонарь?
-
Основания равнобедренной трапеции равны 8 и 18, а периметр 56. Найдите площадь трапеции.
|
Билет №11
-
Дайте определение серединного перпендикуляра к отрезку. Назовите свойство серединного перпендикуляра.
-
Запишите вывод формулы площади треугольника, следствия, формулу Герона (без доказательства).
-
К окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ = 12 см, АО = 13 см. окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ = 12 см, АО = 13 см.
-
На сторонах угла ВАС и на его биссектрисе отложены равные отрезки АВ, АС и AD. Величина угла BDC равна 160о. Определите величину угла ВАС.
|
Билет №12
-
Дайте определение: окружности, вписанной в многоугольник; многоугольника, описанного около окружности. Назовите свойство описанного четырехугольника.
-
Докажите свойства диагоналей ромба.
-
Найдите периметр прямоугольного участка земли, площадь которого равна 800 м2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.
-
Окружность проходит через вершины А и С треугольника АВС и пересекают его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если∠АВС = 20о.
|
Билет №13
-
Дайте определение окружности, описанной около многоугольника; многоугольника, вписанного в окружность. Назовите свойства четырехугольника, вписанного в окружность.
-
Докажите свойство биссектрисы угла.
-
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45о. Найдите площадь треугольника.
-
Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке К. Найдите площадь параллелограмма, если ВС = 19, а расстояние от точки К до стороны АВ равно 7.
|
Билет №14
-
Дайте определение: окружности, вписанной в треугольник; окружности, описанной около треугольника, нахождение центров этих окружностей.
-
Докажите свойство углов при основании равнобедренной трапеции.
-
В выпуклом четырехугольнике ABCD АВ = ВС, AD = CD, ∠В = 60о, ∠D= 110о. Найдите угол А. Ответ дайте в градусах.
-
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30о и 90о.
|
Билет №15
-
Сформулируйте теорему Фалеса.
-
Докажите свойство отрезков пересекающихся хорд.
-
Сторона ромба равна 34, а острый угол равен 60о. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
-
Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
|
 илет №2
илет №2 окажите теорему о средней линии треугольника.
окажите теорему о средней линии треугольника. айдите величину (в градусах) вписанного угла α, опирающегося на хорду АВ, равную радиусу окружности.
айдите величину (в градусах) вписанного угла α, опирающегося на хорду АВ, равную радиусу окружности. окажите свойство отрезков касательных, проведенных к окружности из одной точки.
окажите свойство отрезков касательных, проведенных к окружности из одной точки. окажите признак параллелограмма (по точке пересечения диагоналей).
окажите признак параллелограмма (по точке пересечения диагоналей). айте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
айте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. окажите свойства противоположных сторон и углов параллелограмма.
окажите свойства противоположных сторон и углов параллелограмма. айте определение секущей и касательной к окружности.
айте определение секущей и касательной к окружности.  окажите признак параллелограмма по двум противоположным сторонам, которые равны и параллельны.
окажите признак параллелограмма по двум противоположным сторонам, которые равны и параллельны. окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ = 12 см, АО = 13 см.
окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите радиус окружности, если АВ = 12 см, АО = 13 см.