Файл: Контрольная работа по дисциплине Информатика системы счисления древнего мира байракаев Ф. И студент 1 эттмик зо.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то есть в ней используется только сложение:
 = 800+60+3
= 800+60+3
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
Рисунок 11 – Специальные значки для обозначения больших чисел
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
2.7 Древнеиндийские системы счисления
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

Наряду с этой системой существовала в Индии еще одна система счисления брахми.

Числа брахми записывались слева направо. Однако в обеих системах было немало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.
В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.
2.8 Недостатки непозиционной системы счисления
Непозиционные системы счисления имеют ряд существенных недостатков:
1. Существует постоянная потребность введения новых знаков для записи больших чисел.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.
Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Далее рассмотрим позиционные системы счисления.
3. Позиционные системы счисления
Так записывается число 302, то есть 5*60+2
А это 1*60*60+2*60+5 = 3725.
Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.
Лишь в V веке до нашей эры был введен особый знак - наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.
- наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.
это запись числа 7203 (2*60*60+3)
Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так

 , а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.
, а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.
Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под шестидесятеричную систему семитов.
Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.
3.2 Древнекитайская десятеричная
Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.
Для того чтобы не перепутать буквы и цифры, использовались титла - горизонтальные черточки над числами, что мы видим на рисунке.
Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:
| | Тысяча | 1000 |
| | Тьма | 10 000 |
| | Легион | 100 000 |
| | Леодр | 1 000 000 |
| | Ворон | 10 000 000 |
| | Колода | 100 000 000 |
Рисунок 11 – Специальные значки для обозначения больших чисел
Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.
2.7 Древнеиндийские системы счисления
Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления. О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево.

Наряду с этой системой существовала в Индии еще одна система счисления брахми.

Числа брахми записывались слева направо. Однако в обеих системах было немало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы.
В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света». Например, число 2441 произносилось так: глаза океанов стороны света луны.
2.8 Недостатки непозиционной системы счисления
Непозиционные системы счисления имеют ряд существенных недостатков:
1. Существует постоянная потребность введения новых знаков для записи больших чисел.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.
Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Далее рассмотрим позиционные системы счисления.
3. Позиционные системы счисления
3.1 Вавилонская десятеричная / шестидесятеричная
В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления - числа менее 60 обозначались с помощью двух знаков: 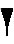 для единицы, и
для единицы, и 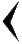 для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например
для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например
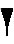
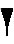
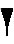 - 3;
- 3; 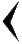
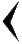 - 20;
- 20; 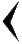
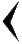
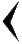
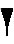
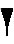 - 32;
- 32; 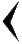
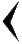
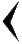
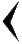
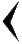
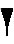
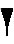
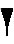
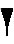
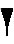
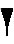
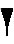
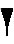
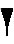 -
-
59
Числа больше 60 записывались по разрядам, с небольшими пробелами между ними:
| | |
Так записывается число 302, то есть 5*60+2
| | | | 1*60*60+2*60+5 = 3725 |
А это 1*60*60+2*60+5 = 3725.
Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.
Лишь в V веке до нашей эры был введен особый знак
| | | | 2*60*60+3 = 7203 |
это запись числа 7203 (2*60*60+3)
Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так
Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под шестидесятеричную систему семитов.
Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.
3.2 Древнекитайская десятеричная
Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда - кружок - аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.
| | 1 | | 6 |
| | 2 | | 7 |
| | 3 | | 8 |
| | 4 | | 9 |
| | 5 | O | 0 |