Файл: Контрольная работа по дисциплине Информатика системы счисления древнего мира байракаев Ф. И студент 1 эттмик зо.docx

10	100	1 000	10 000

Рисунок 12 - Древнекитайская десятеричная система счисления

4.3 Двадцатеричная система счисления индейцев Майя или долгий счет

Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).



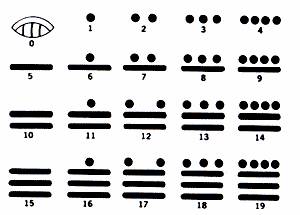
У индейцев Майя 20 дней-кинов образовывали месяц или уинал. 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:

К'ин = 1 день. Виналь = 20 к'ин = 20 дней. Тун = 18 виналь = 360 дней = около 1 года. К'атун = 20 тун = 7200 дней = около 20 лет. Бак'тун = 20 к'атун = 144000 дней = около 400 лет. Пиктун = 20 бак'тун = 2880000 дней = около 8000 лет. Калабтун = 20 пиктун = 57 600 000 дней = около 160000 лет. К'инчильтун = 20 калабтун = 1152000000 дней = около 3200000 лет. Алавтун = 20 к'инчильтун = 23040000000 дней = около 64000000 лет.



Рисунок 13 – Пример обозначения количества дней

Это довольно сложная система счисления, в основном использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.

4. История «арабских» чисел

История наших привычных «арабских» чисел очень запутана. Нельзя сказать точно и достоверно, как они произошли. Вот один из вариантов этого истории этого происхождения. Одно точно известно, что именно благодаря древним астрономам, а именно их точным расчетам мы и имеем наши числа.

---

Как мы уже знаем, в вавилонской системе счисления присутствует знак для обозначения пропущенных разрядов. Примерно во II веке до н.э. с астрономическими наблюдениями вавилонян познакомились греческие астрономы (например, Клавдий Птолемей). Они переняли их позиционную систему счисления, но целые числа они записывали не с помощью клиньев, а в своей алфавитной нумерации, а дроби в вавилонской шестидесятеричной системой счисления. Но для обозначения нулевого значения разряда греческие астрономы стали использовать символ "0" (первая буква греческого слова Ouden - ничто).

Между II и VI веками н.э. индийские астрономы познакомились с греческой астрономией. Они переняли шестидесятеричную систему и круглый греческий нуль. Индийцы соединили принципы греческой нумерации с десятичной мультипликативной системой взятой из Китая. Так же они стали обозначать цифры одним знаком, как было принято в древнеиндийской нумерации брахми. Это и был завершающий шаг в создании позиционной десятичной системы счисления.

Блестящая работа индийских математиков была воспринята арабскими математиками и Аль-Хорезми в IX веке написал книгу "Индийское искусство счета", в которой описывает десятичную позиционную систему счисления. Простые и удобные правила сложения и вычитания сколь угодно больших чисел, записанных в позиционной системе, сделали ее особенно популярной в среде европейских купцов.

В XII в. Хуан из Севильи перевел на латынь книгу "Индийское искусство счета", и индийская система счета широко распространилась по всей Европе. А так как труд Аль-Хорезми был написан арабском языке, то за индийской нумерацией в Европе закрепилось неправильное название - "арабская". Но сами арабы именуют цифры индийскими, а арифметику, основанную на десятичной системе - индийским счетом.

5. История нуля

Нуль бывает разный. Во-первых, нуль – это цифра, которая используется для обозначения пустого разряда; во-вторых, нуль – это необычное число, так как на нуль делить нельзя и при умножении на нуль любое число становиться нулем; в-третьих, нуль нужен для вычитания и сложения, иначе, сколько будет, если из 5 вычесть 5?

Впервые нуль появился в древневавилонской системе счисления, он использовался для обозначения пропущенных разрядов в числах, но такие числа как 1 и 10 у них записывали одинаково, так как нуль в конце числа у них не ставился. В их системе нуль выполнял роль пробела в тексте.

---

Изобретателем формы нуля можно считать великого греческого астронома Птолемея, так как в его текстах на месте знака пробела стоит греческая буква омикрон, очень напоминающая современный знак нуля. Но Птолемей использует нуль в том же смысле, что и вавилоняне.

На стенной надписи в Индии в IX веке н.э. впервые символ нуля встречается в конце числа. Это первое общепринятое обозначение современного знака нуля. Именно индийские математики изобрели нуль во всех его трех смыслах. Например, индийский математик Брахмагупта еще в VII века н.э. активно стал использовать отрицательные числа и действия с нулем. Но он утверждал, что число, деленное на нуль, есть нуль, что конечно ошибка, но настоящая математическая дерзость, которая привела к другому замечательному открытию индийских математиков. И в XII веке другой индийский математик Бхаскара делает еще попытку понять, что же будет при делении на нуль. Он пишет: "количество, деленное на нуль, становится дробью, знаменатель которой равен нулю. Эту дробь называют бесконечностью".

Леонардо Фибоначчи, в своем сочинении "Liber abaci" (1202) называет знак 0 по-арабски zephirum. Слово zephirum – это арабское слово as-sifr, которое произошло от индийского слова sunya, т. е. пустое, служившего названием нуля. От слова zephirum произошло французское слово zero (нуль) и итальянское слово zero. С другой стороны, от арабского слова as-sifr произошло русское слово цифра. Вплоть до середины XVII века это слово употреблялось специально для обозначения нуля. Латинское слово nullus (никакой) вошло в обиход для обозначения нуля в XVI веке.

Нуль - это уникальный знак. Нуль – это чисто абстрактное понятие, одно из величайших достижений человека. Его нет в природе окружающей нас. Без нуля можно спокойно обойтись в устном счете, но невозможно обойтись для точной записи чисел. Кроме этого, нуль находится в противовесе всем остальным числам, и символизирует собой бесконечный мир. И если “все есть число”, то ничто есть все!

Заключение

В заключение могу сказать, что в разных системах счисления есть схожие элементы, например, наличие нуля (как в Древнекитайской десятеричной системе счисления и двадцатеричной системе счисления индейцев Майя), счет путем добавления палочек (как в Древнеегипетской десятеричной, Римской пятеричной и Древнегреческой аттической пятеричной системах счисления), замена чисел на алфавитные символы с добавлением титлы (как в Древнегреческой ионийской десятеричной алфавитной и Славянской кириллической десятеричной алфавитной системах счисления). Также не могу не отметить, что в некоторых системах счисления отсутствует обозначение нуля, как абстрактного понятия. Тем самым люди усложняли систему счета, добавляя все новые и новые элементы, обозначающие десятки. Исследуя системы счисления Древнего мира, я сделала вывод, что каждая система по-своему хороша, но также имеет свои недостатки. Также я считаю, что человечество выбрало самый эффективный метод счета с помощью арабской системы счисления, потому что она наиболее удобна в использовании современным обществом.

---

Список использованной литературы

1. В. Лёвшин, Три дня в Карликании, 1966

2. Всевозможные нумерации и системы счисления (http://www.megalink.ru/agb/n/numerat.htm)

3. А.П. Юшкевич, История математики, Том 1, 1970

4. Г.И. Глейзер, История математики в школе, 1964

5. И.Я. Депман, История арифметики, 1965

6. А. Костинский, В. Губайловский, Триединый нуль (http://www.svoboda.org/programs/sc/2004/sc.011304.asp)

7. Кузьмищев В.А. Тайна жрецов майя. 2-е изд. — М., «Молодая гвардия», 1975

---