Файл: Лекция Уравнение плоскости в пространстве Общее уравнение плоскости.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.02.2024

Просмотров: 48

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Лекция: Уравнение плоскости в пространстве

  1. Общее уравнение плоскости

Плоскостью называется поверхность, все точки которой удовлетворяют уравнению Ax + By + Cz + D = 0, где А, В, С – координаты вектора -вектор нормали к плоскости.

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz



  1. Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору



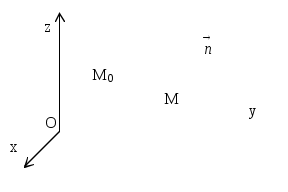
Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – x0) + B(y – y0) + C(z – z0) = 0.


  1. Уравнение плоскости в отрезках

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)

, заменив , получим уравнение плоскости в отрезках: .

Ч 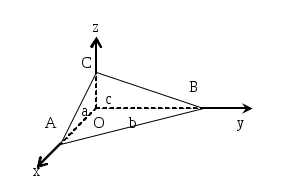исла a, b, c являются точками пересечения плоскости соответственно с осями
х, у, z.



  1. Уравнение плоскости в векторной форме (нормальное уравнение)

Пусть - радиус-вектор текущей точки М(х, у, z), - единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат. , и - углы, образованные этим вектором с осями х, у, z. p – длина этого перпендикуляра.



В координатах это уравнение имеет вид: xcos + ycos + zcos - p = 0, где .

Из общего уравнения можно перейти к нормальному уравнению, если умножить обе части уравнения на множитель , где знак берется противоположным знаку свободного члена общего уравнения.


  1. Уравнение плоскости, проходящей через три точки

Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы были компланарны. Таким образом,

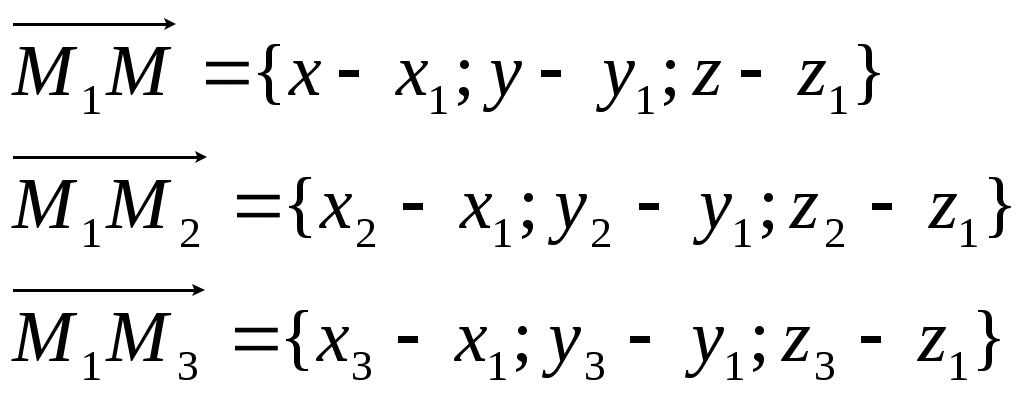
Уравнение плоскости, проходящей через три точки:

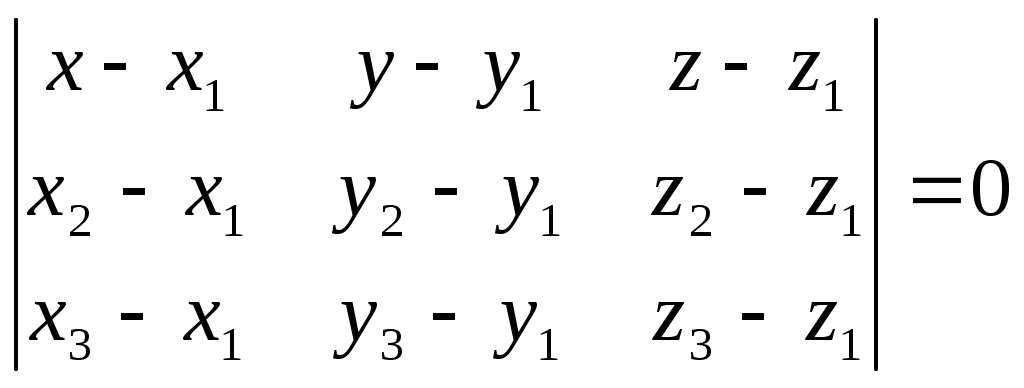
Пример.

Найти уравнение плоскости, проходящей через точки , ,. .

Воспользуемся выше предложенной формулой:




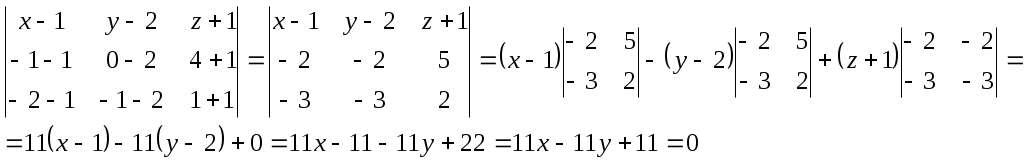
Получаем уравнение плоскости


  1. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости

Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор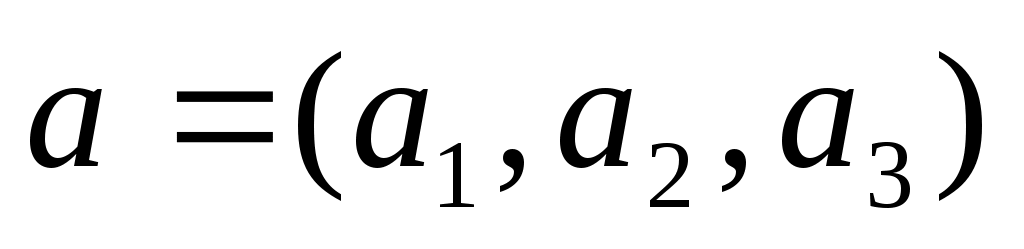 . Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору .


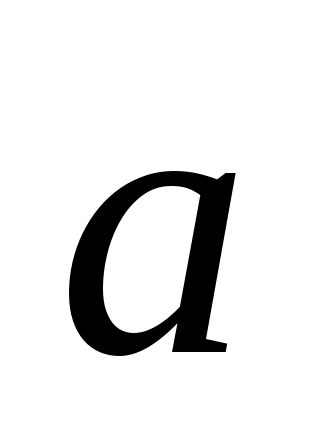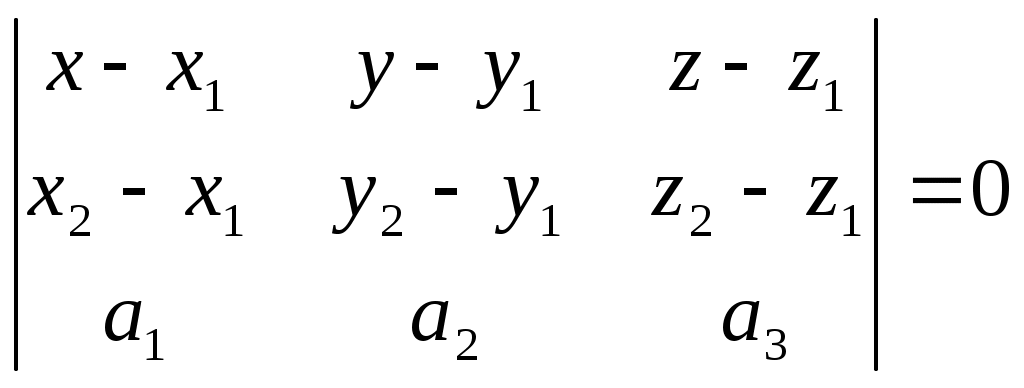
Векторы и вектор должны быть компланарны. Уравнение плоскости:


  1. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости

Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.

Уравнение плоскости: .
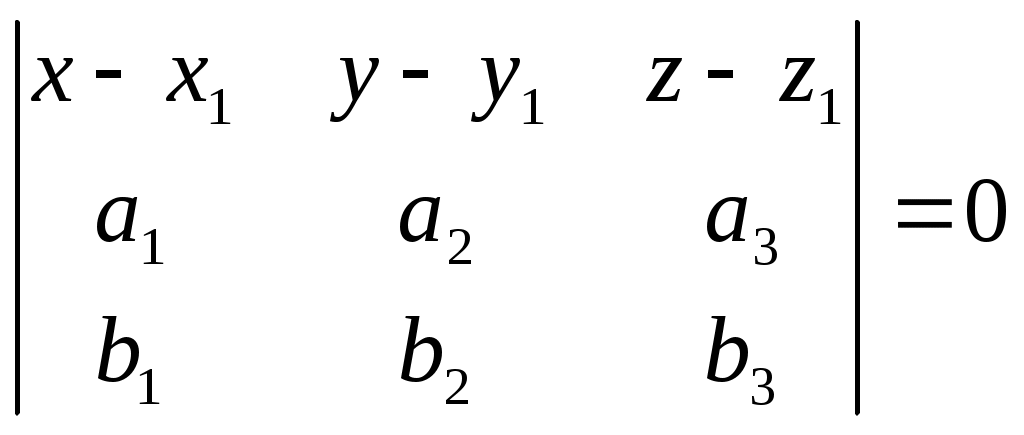Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости (A, B, C). Вектор
(1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то



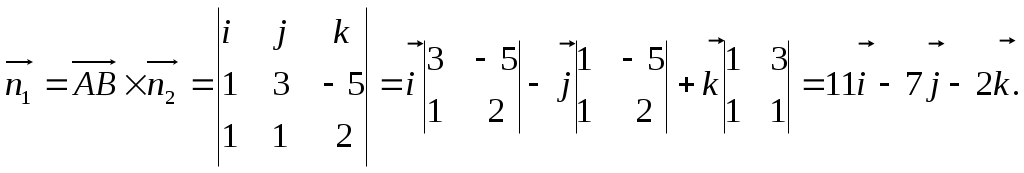
Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 112 + 71 - 24 + D = 0; D = -21. Итого, получаем уравнение плоскости: 11x - 7y – 2z – 21 = 0


  1. Расстояние от точки до плоскости

Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно


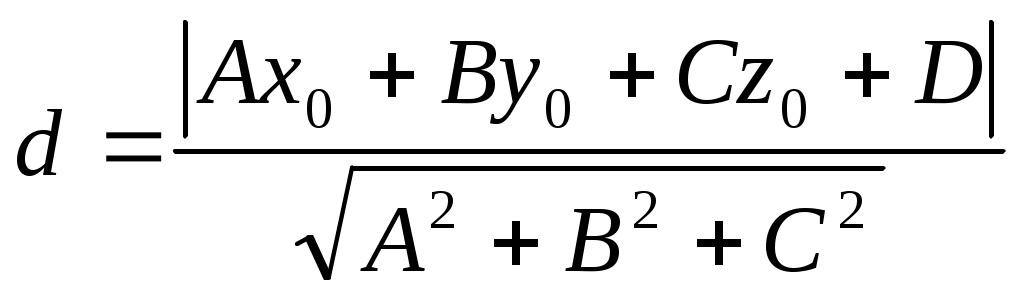
  1. Угол между плоскостями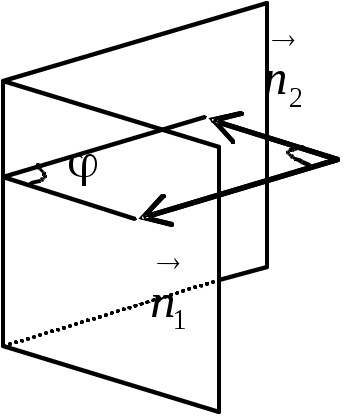

Угол между двумя плоскостями в пространстве  - это двугранный угол образованный этими плоскостями.

Этот угол связан с углом между нормалями к этим плоскостям, где (A1, B1, C1), (A2, B2, C2).

Угол между векторами нормали найдем из их скалярного произведения: 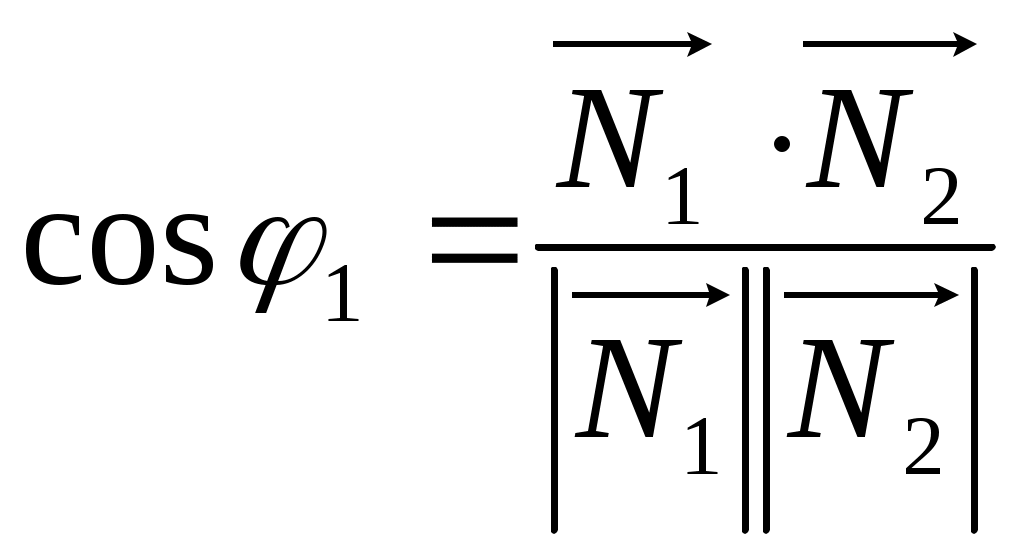. Таким образом, угол между плоскостями находится по формуле: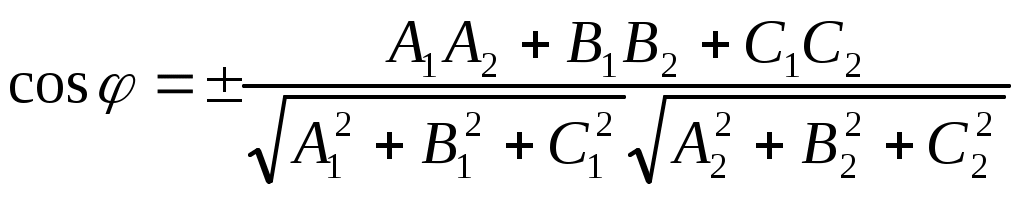

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой

Пример:

Найти угол между плоскостями и .

Находим нормали к плоскостям:
,

По формуле



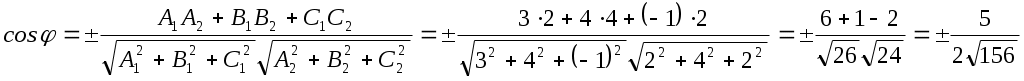
Ответ: .

  1. Условия параллельности и перпендикулярности плоскостей

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

Для того, чтобы плоскости были перпендикулярны, необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если: .

Плоскости параллельны, если векторы нормалей коллинеарны:  .Это условие выполняется если: .


Задания для самостоятельной работы:

1. Даны уравнения плоскостей

1.

5.

9.

2.

6.

10.

3.

7.

11.

4.

8.

12.

Смотрите также файлы