Файл: Лабораторная работа 1 Определение аэродинамических характеристик осесимметричного тела.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 101
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д.Ф. УСТИНОВА
Дисциплина Механика жидкости и газа
Лабораторная работа № 1
Определение аэродинамических характеристик
осесимметричного тела
| Выполнил студент | Баранова А. А. | |||
| Фамилия И.О. | ||||
| группа | А491 | | ||
| | ||||
| Преподаватель | Горохова П.Д. | |||
| | Фамилия И. О. | |||
| | Подпись преподавателя | Дата | ||
| Допуск | | | ||
| Выполнение | | | ||
| Защита | | | ||
Санкт-Петербург
2021 г.
Цель работы – определить аэродинамические коэффициенты cx, cy и cmz осесимметричного оперенного тела вращения в функции от угла атаки α, найти положение центра давления относительно центра тяжести в зависимости от угла атаки α. Силовое воздействие потока на модель тела вращения определить с помощью замера сил на аэродинамических весах.
Рис.1. Чертеж модели
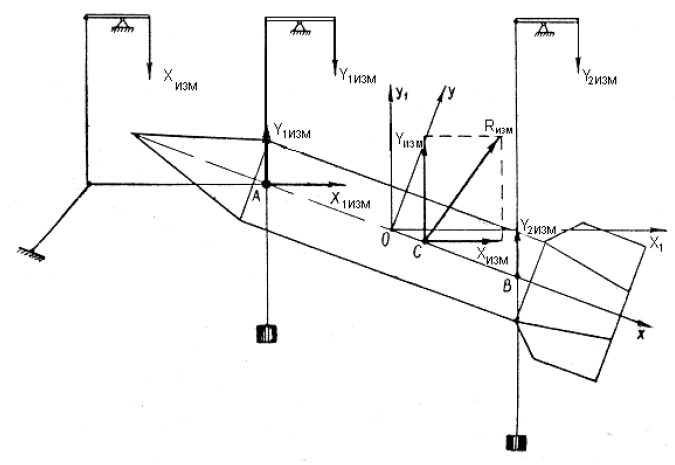
Рис.2. Схема сил и координатных осей
В ходе выполнения лабораторной работы были сняты необходимые для расчета данные
, указанные в таб.1.
Таблица 1
| Α | 0̊ | 4̊ | 8̊ | 12̊ |
| Xизм , ГС | 180 | 197 | 261 | 420 |
| Y1изм , ГС | 0 | 35 | 55 | -32 |
| Y2изм , ГС | 0 | 265 | 670 | 1180 |
| Δhn ,мм | 155 | 153 | 153 | 150 |
1. Расчет силы лобового сопротивления, составляющие подъемной силы и саму подъемную силу по формулам:
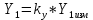
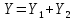
При α=0̊
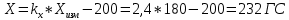
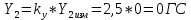
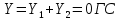
При α=4̊
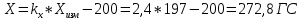
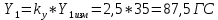
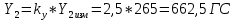
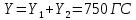
При α=8̊
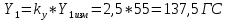
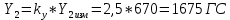
При α=12̊
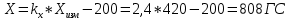
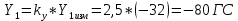
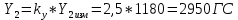
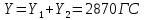
2. Вычисление площади поперечного сечения миделя модели, скоростной напор и скорость натекающего потока
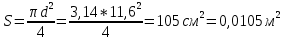
Скоростной напор рассчитывается по формуле:
Для расчета скоростного напора стоит использовать среднее значение
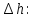
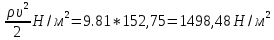
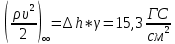
Зная скоростной напор, вычисляем скорость натекающего потока
3. После определения значения
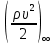найдем аэродинамические коэффициенты сх, cy и cy2 по формулам:
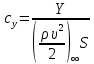
При α=0̊
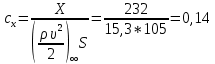
При α=4̊
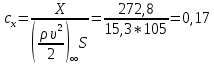
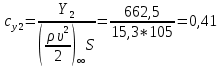
При α=8̊
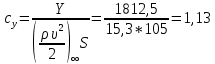
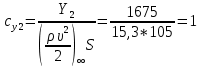
При α=12̊
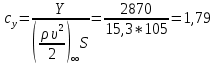
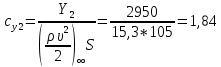
4. Найдем значения коэффициентов cx0, a1, a2, a3, a4, a5 с помощью обработки экспериментальных данных методом наименьших квадратов, будем брать угол α в радианах.
;
;
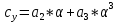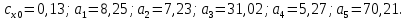
5. Определение положение центра давления С.
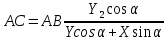
Разделим числитель и знаменатель дроби на
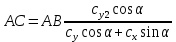
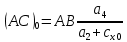
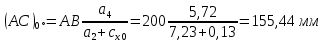
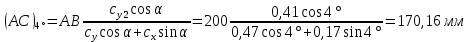
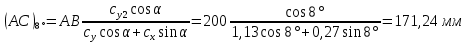
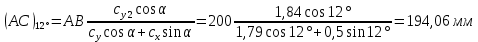
Найденное соотношение дает положение центра давления С на оси тела вращения относительно точки А. Необходимо ориентировать точку С относительно центра тяжести. Поэтому нужно найти центр тяжести всей модели в целом. В частности, для простоты можно считать модель сплошной и однородной, состоящей из трех составных частей: носовой (1), центральной (2) и кормовой (3) (весом оперения пренебрегаем).
6. Определение положения центра тяжести.
Для круглого прямого усеченного конуса:
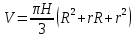
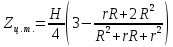
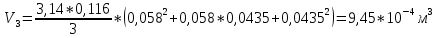
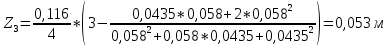
Для полного конуса (r=0):
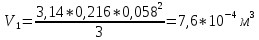
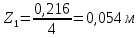
Для цилиндра:
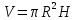
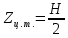
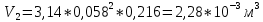
Положение центра тяжести модели х0определяется по формуле:
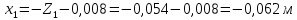
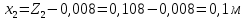
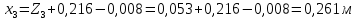
7. Определение расстояния вдоль оси между центром тяжести и центром давления:
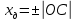, где 
, если точка С находится перед точкой О.
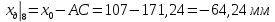
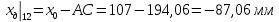
8. Определение значения коэффициента сmz для каждого угла атаки и коэффициенты аппроксимирующего зависимость сmz= сmz(α) полинома.
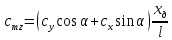
При α=0̊
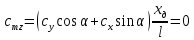
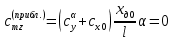
При α=4̊
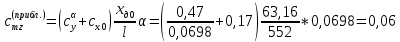
При α=8̊
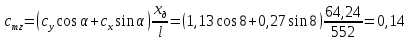
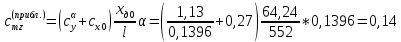
При α=12̊
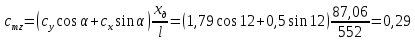
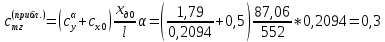
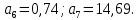
Полученные в расчетах данные заносим в таблицу 1.
Таблица 1. «Результаты вычислений»
| α | 0̊ | 4̊ | 8̊ | 12̊ |
| Xизм , ГС | 180 | 197 | 261 | 420 |
| Y1изм , ГС | 0 | 35 | 55 | -32 |
| Y2изм , ГС | 0 | 265 | 670 | 1180 |
| Δhn ,мм | 155 | 153 | 153 | 150 |
| X , ГС | 232 | 272,8 | 426,4 | 808 |
| Y1 , ГС | 0 | 87,5 | 137,5 | -80 |
| Y2 , ГС | 0 | 662,5 | 1675 | 2950 |
| Y , ГС | 0 | 750 | 1812,5 | 2870 |
| AC , мм | 155,44 | 170,16 | 171,24 | 194,06 |
| Xg , мм | 48,44 | 63,16 | 64,24 | 87,06 |
| Cx | 0,14 | 0,17 | 0,27 | 0,5 |
| Cy | 0 | 0,47 | 1,13 | 1,79 |
| Cmz | 0 | 0,06 | 0,14 | 0,29 |
| Cmz пр | 0 | 0,06 | 0,14 | 0,3 |
| K=Cy /Cx | 0 | 2,77 | 4,19 | 3,58 |