ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИГосударственное образовательное учреждение высшего профессионального образованияМосковский технический университет связи и информатикиЧисленные методыЛабораторная работа №1«Применение базовых средств пакета MATHCADдля решения нелинейных уравнений»Выполнил: Казак И.А.Группа: БИН2152 Вариант: 9Москва, 2023 г.Задание

1. 
   Выбрать индивидуальное задание.
   
2. 
   Отделить корни уравнения.
   
3. 
   Уточнить корень уравнения 4-мя численными методами, для чего для каждого метода:
   

1. 
   проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;
   
2. 
   выбрать начальное приближение;
   
3. 
   сформулировать условия окончания этапа уточнения корня.
   

4. 
   Провести расчет трех итераций (без использования панели инструментов «Программирование»).
   
5. 
   Оценить погрешность результата расчета.
   
6. 
   Решить нелинейное уравнение встроенными средствами математического пакета.
   

Решение1. Задание для решения нелинейных уравнений:

• 
  уравнение ;
  
• 
  методы решения нелинейных уравнений – половинного деления, итерации, Ньютона и хорд;
  

2. 
   Отделение корней с использованием MathCad
   

Отделение корней производим графическим методом (график функции) с обязательным подтверждением результата аналитически (таблица).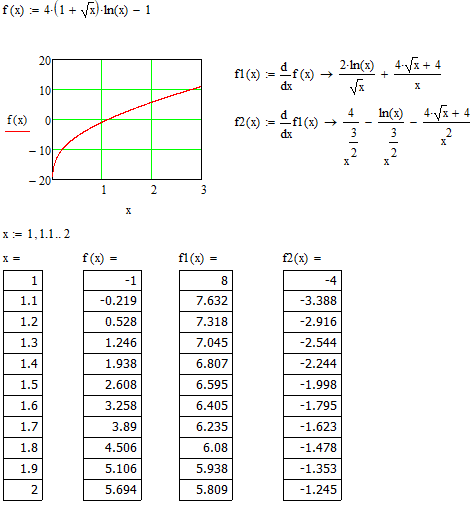На отрезке [1; 2] функция f(x) меняет знак, т.е. существует, по крайней ере, один корень. Поскольку знак первой производной f1(x) >0 на выбранном отрезке остается постоянным, то можно сказать, что функция на этом отрезке

---

монотонна. Знакопостоянство второй производной f2(x)<0 на выбранном отрезке является необходимым условием применения метода Ньютона и метода хорд. Следовательно, уравнение имеет единственный корень на отрезке [1;2].3.Уточнение корня с использованием MathCadМетод половинного деления

1. 
   Исследование задания
   

• 
  Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [1;2] функция меняет знак ( ) и монотонна (f^′(x)<0), то условие сходимости выполняется.
  
• 
  Выберем за начальное приближение середину отрезка
  

=1.5.

• 
  Условие окончания процесса уточнения корня. Для оценки погрешности метода половинного деления справедливо условие
  

|b_n – a_n|<ε , т.е. длина отрезка, полученного на n-ом шаге должна быть меньше заданной точности -

2. 
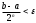
   Результаты «ручного расчета» трех итераций
   

Результаты вычислений представлены в форме табл. 1-2а.

n	an	bn	f(an)	f(bn)	(an+bn)/2	f( (an+bn)/2)	bn-an
0	1	2	-1	5.694	1.5	2.608	1
1	1	1.5	-1	2.608	1.25	0.891	0.5
2	1	1.25	-1	0.891	1.125	-0.029	0.25
3	1.125	1.25					0.125

---

После трех итераций приближение к корню середина [a₃, b₃] - x₃=1.187.3) Погрешность численного решения нелинейных уравненийОценим погрешность результата после трех итераций: r = | b₃ – a₃ |=0.125. Округлим eё в большую(!) сторону – до первой слева ненулевой цифры – | b₃ – a₃ |=0.2 Согласуем/округлим решение (x₃ ) по числу знаков в погрешности. Получим:ОТВЕТ: после 3-х итераций корень уравнения равен x₃ r = 1.19 0,2Метод итераций1) Исследование задания.

• 
  Приведем уравнение f(x)=0 к виду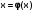 . Тогда рекуррентная формула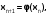 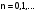. Для сходимости процесса итерации необходимо, чтобы 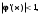при 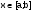. Если 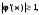то сходимость не обеспечена.
  

Приведем уравнение к виду x = 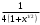и проведем исследование.

---

В приведенном примере условие сходимости выполняется и можно использовать итерирующую/итерационную функцию 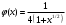в рекуррентной формуле для уточнения корня методом итераций, что и будет показано ниже. Однако, в случаях, когда свободный х выразить не удается, или когда целесообразно воспользоваться следующим приемом, позволяющим обеспечить выполнение условий сходимости.

• 
  Выбор начального приближения к корню. В методе итераций x₀ – произвольное значение из отрезка [a;b], например, x₀=1
  
• 
  Условие окончания процесса уточнения корня. Для оценки погрешности метода итерации справедливо соотношение:
  

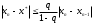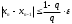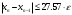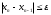
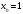
. Итерации следует продолжать до тех пор, пока не выполнится условие останова: , где q=max |φ′(x)| на выбранном отрезке, ε – заданная точность. В нашем случае q=max|φ′(x)|= =0.035. Тогда условие останова будет Если q<1/2, то можно использовать условие 2) «Ручной расчет» трех итерацийДля получения решения уравнения методом итерации необходимо воспользоваться следующей рекуррентной формулой: ,Результаты вычислений представлены в форме табл. 1-2б.

к	Xк	f(xк)
0	1	-1
1	1.133	0.032
2	1.129	-1.066 • 10-3
3	1.129	3.14 • 10-5

---

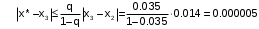
Сходимость итерационного процесса подтверждается принадлежностью всех X_к выбранному исходному отрезку изоляции корня [1;2] и стремлением f(x_к) к нулю.Примечание: Если свободный х выразить не удается или когда то применяется формула с использованиемλ.3) Погрешность численного решения нелинейного уравненияОценим погрешность результата после трех итераций: .Аналогично предыдущему методу, округлим погрешность решения (r=0.000005). Здесь погрешность возникает уже в 3-ем знаке после запятой. Округлим/согласуем решение (x₃ ) по числу знаков после запятой в погрешности. Окончательно получим:ОТВЕТ: после 3-х итераций корень уравнения равен x₃ r= 1.129 0,000005Метод Ньютона1) Исследование задания.

• 
  Необходимые и достаточные условия сходимости метода Ньютона:
  

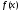непрерывна на [a;b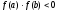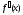] и ; и 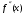отличны от нуля и сохраняют знаки для 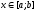.В нашем случае на отрезке [1;2] требования сходимости выполняются.

• 
  Начальное приближение должно удовлетворять условию: 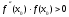, т.е. за начальное приближение следует принять тот конец отрезка, где знак функции и знак второй производной совпадают. Поскольку < 0 и > 0, то выберем начальное приближение к корню: =2.
  
• 
  Условие окончания процесса уточнения корня. Для оценки погрешности метода Ньютона справедливо соотношение: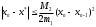 , где M₂ – наибольшее значение 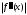, m₁ –наименьшее значение на отрезке[a;b]. Из требования обеспечения точности ε следует условие окончания вычислений
  

---

Смотрите также файлы

• Научнообразовательный журнал для студентов и преподавателей.docx

• Сабаты таырыбы Кестелі мліметтерді графикалы сынылуы.docx

• В данном докладе рассмотрена структура и сущностные характеристики познавательных универсальных учебных действий школьников, система заданий, формирующая познавательные ууд на уроках русского языка.docx

• Конспект занятия по фэмп Деление круга на четыре равные части.docx

• Модель компетенций выпускника.doc