Формулы дифференцирования
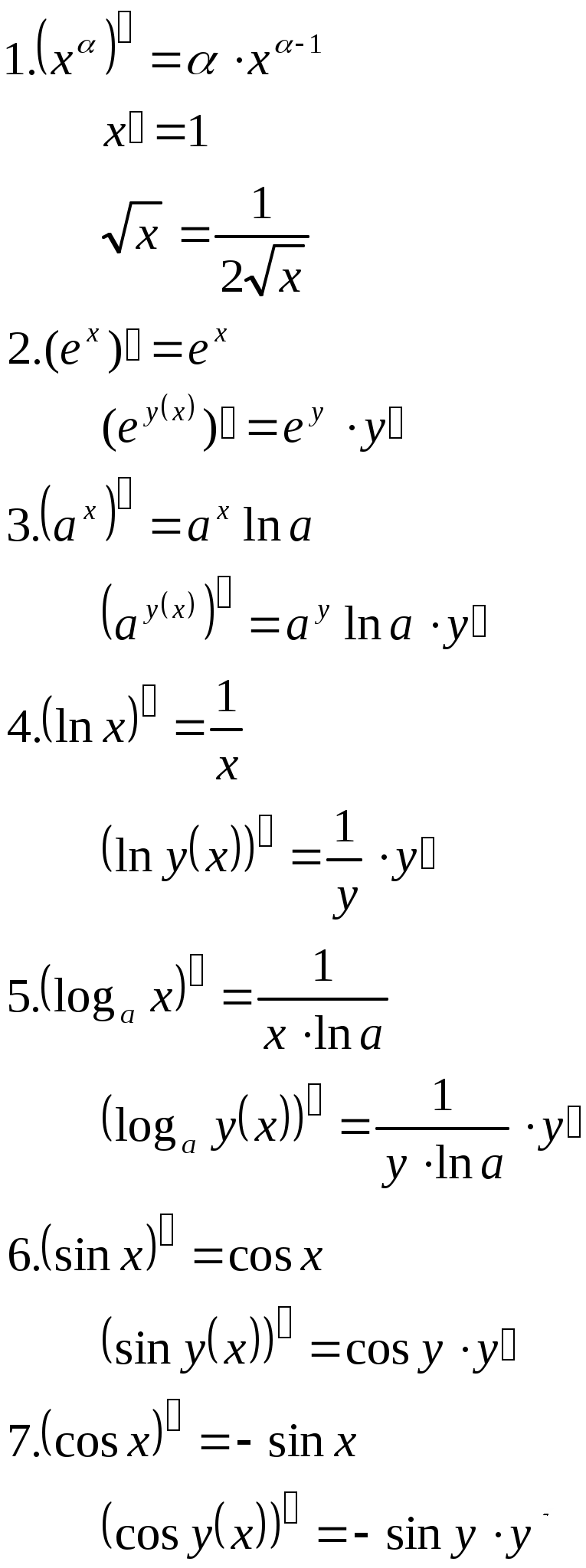Правила дифференцирования
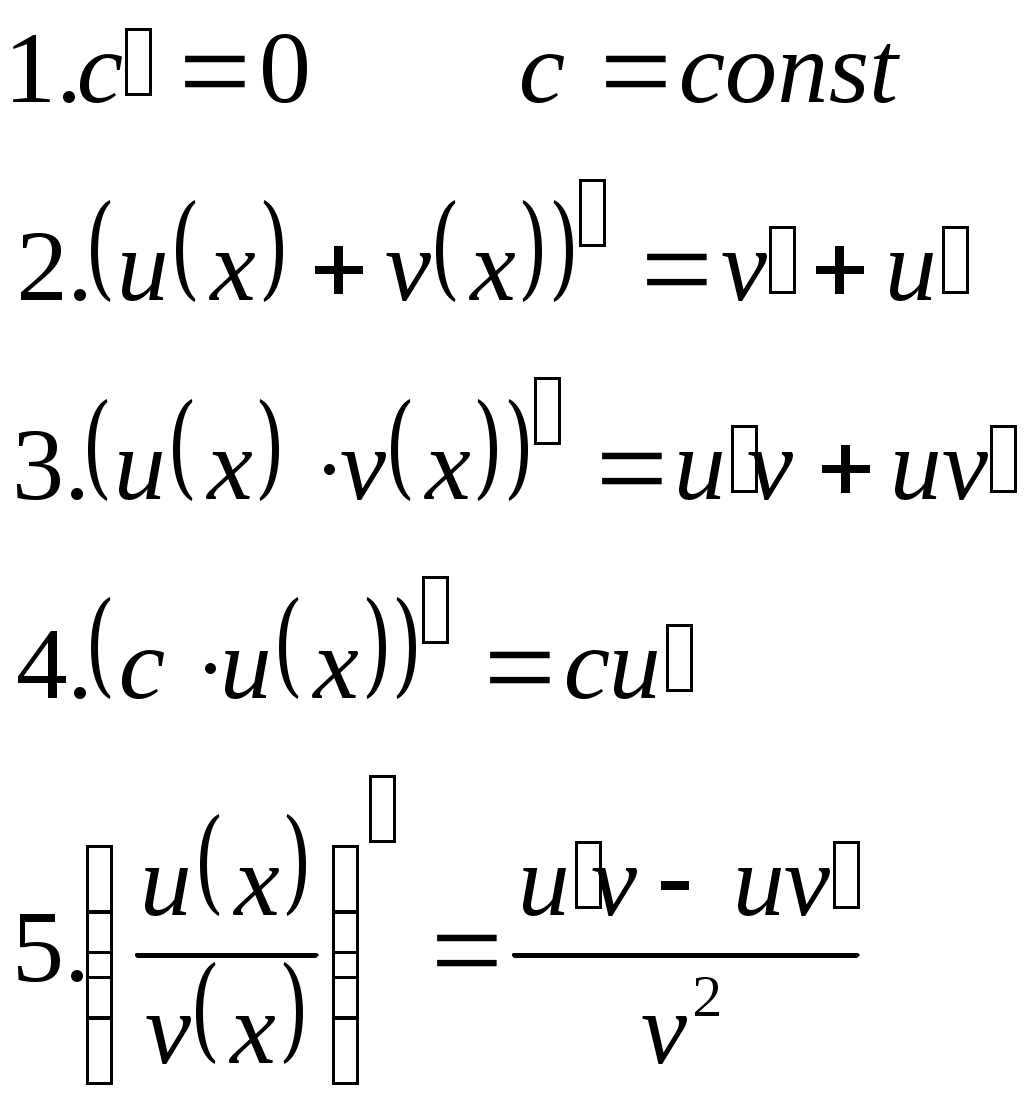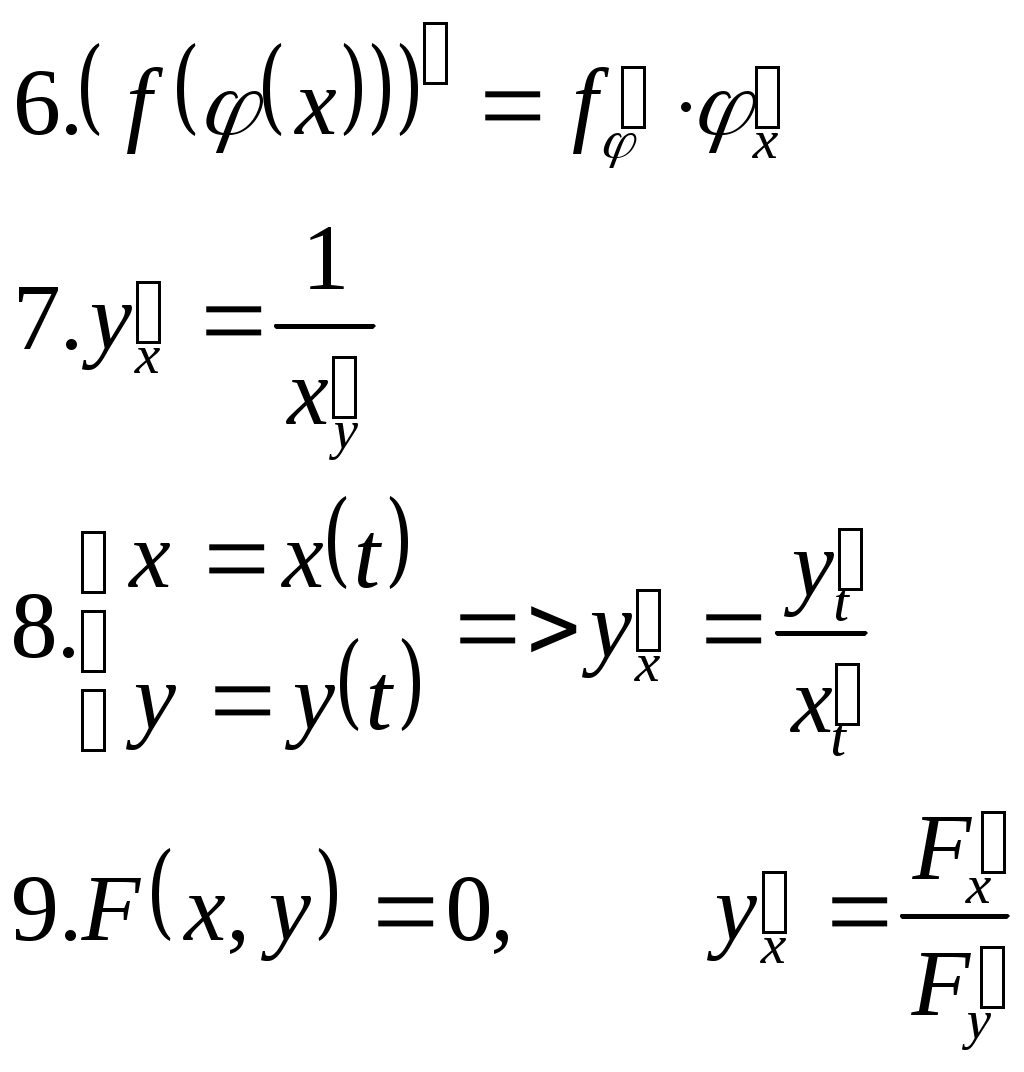Г иперболические функции
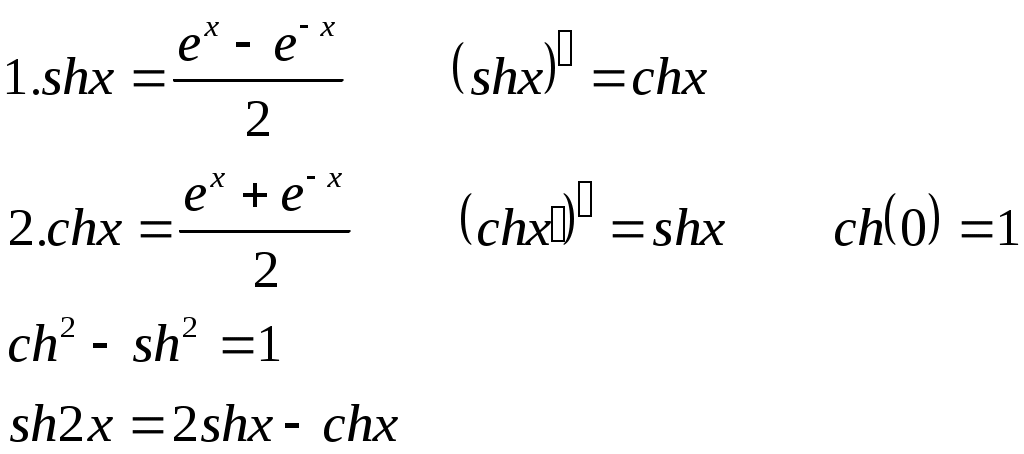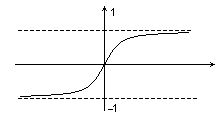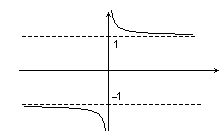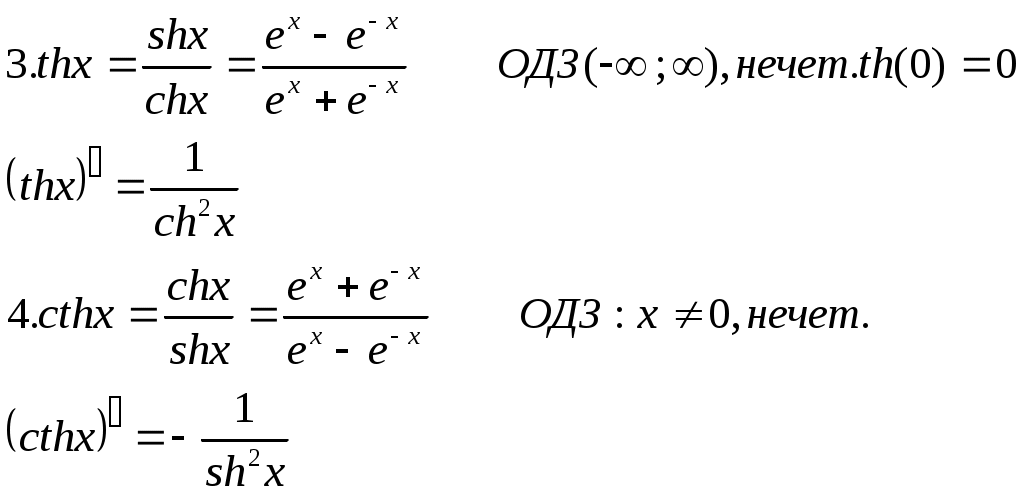Свойства неопределенных интегралов
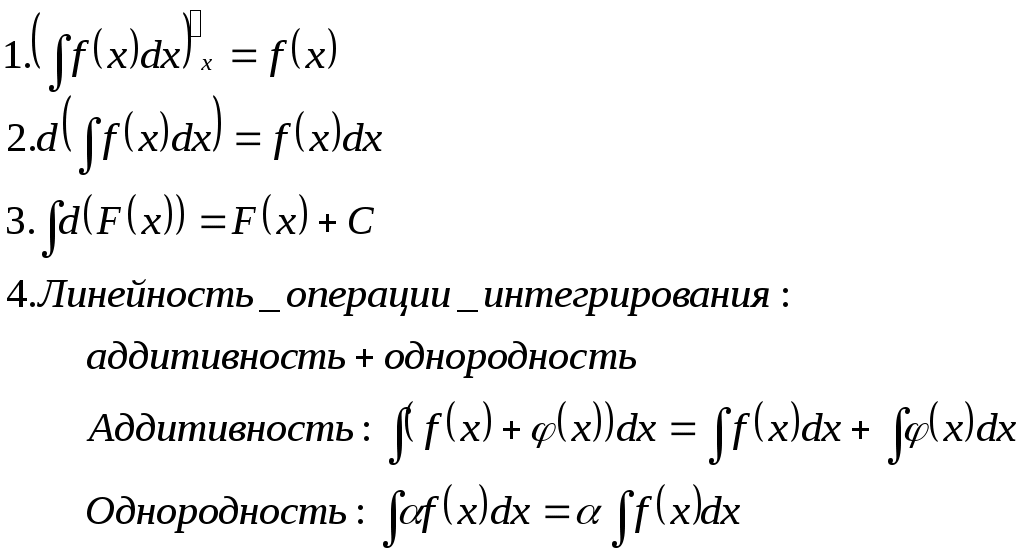Таблица неопределенных интегралов
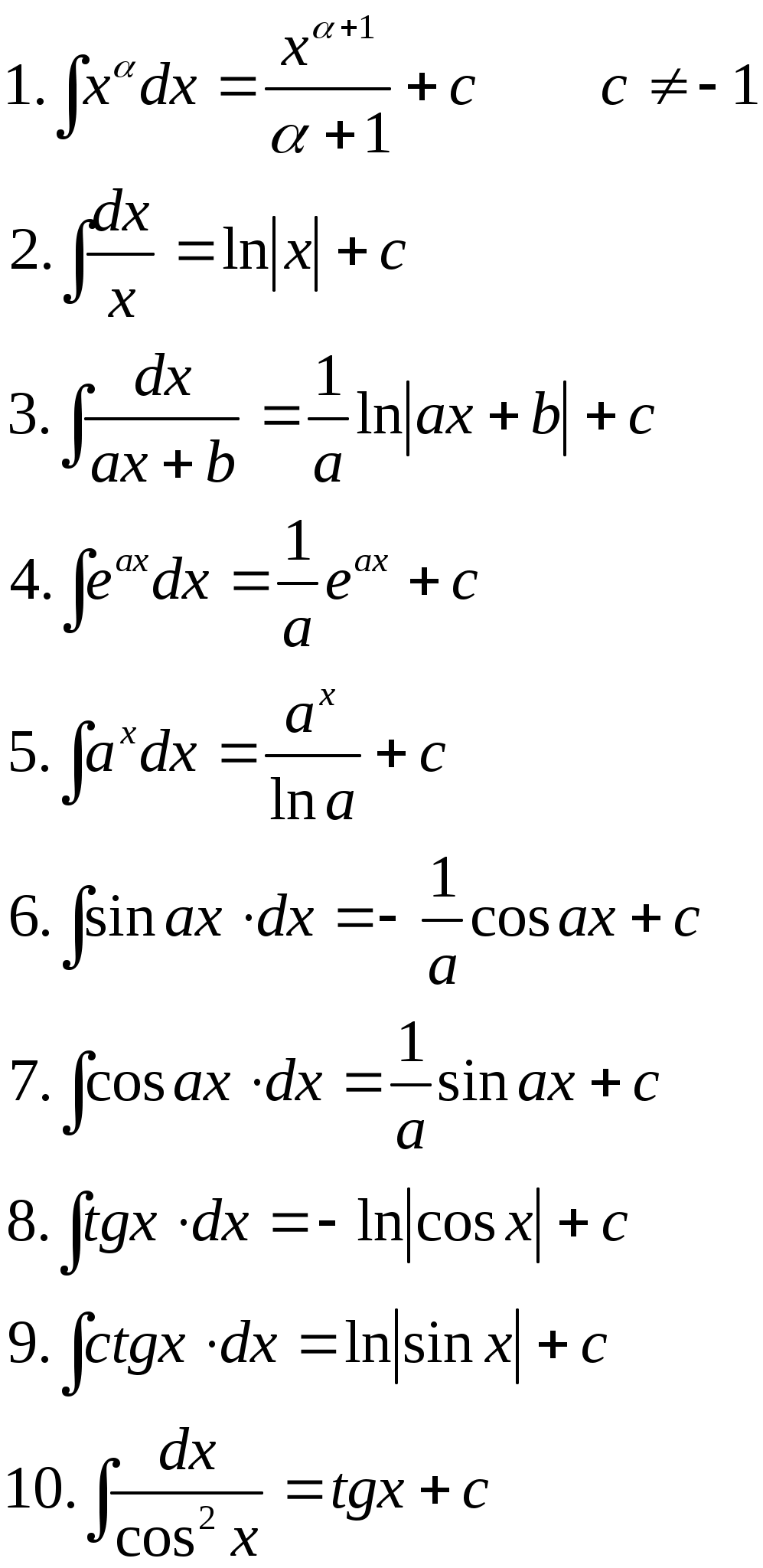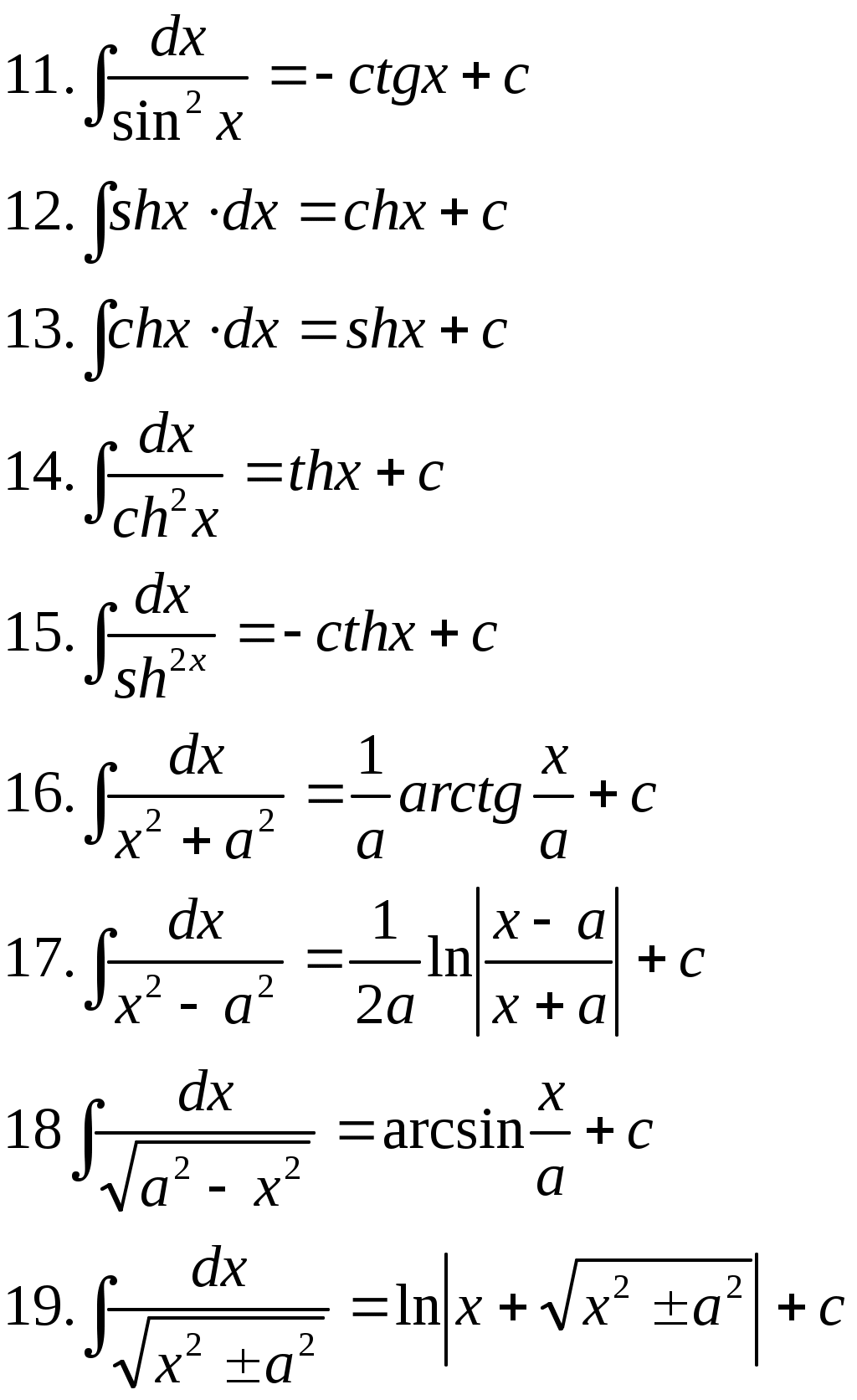Интегрирование по частям
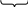u dv 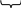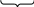u dv 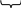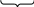u dv 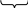u dv k=1,2… α Q				u dv u dv круговые Замечание: необходимо два раза проинтегрировать по частям, при этом оба раза за u(x) обозначают функции одного типа: либо показательную, либо промежуточную.
Интегрирование тригонометрических выражений
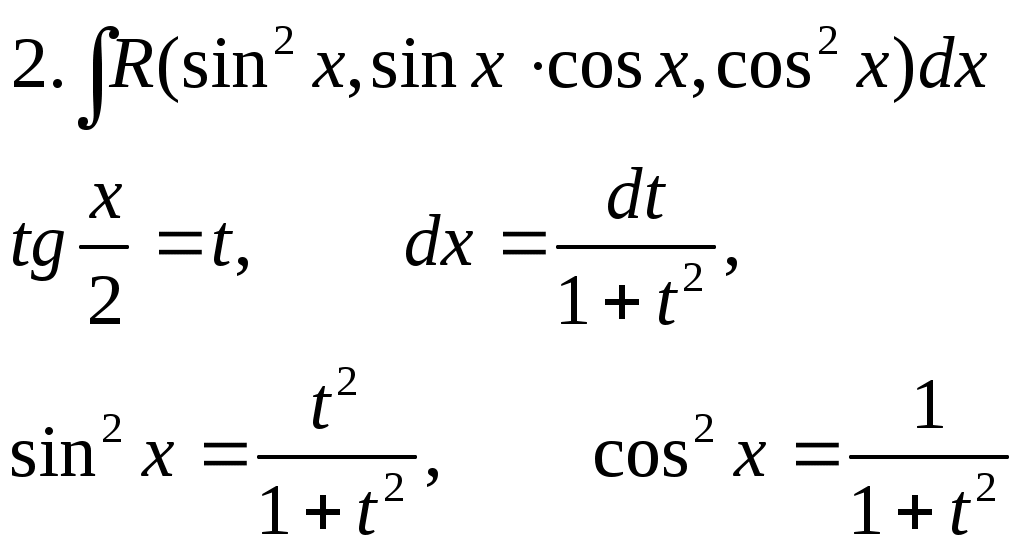то переходят к той функции , которая стоит в четной степени.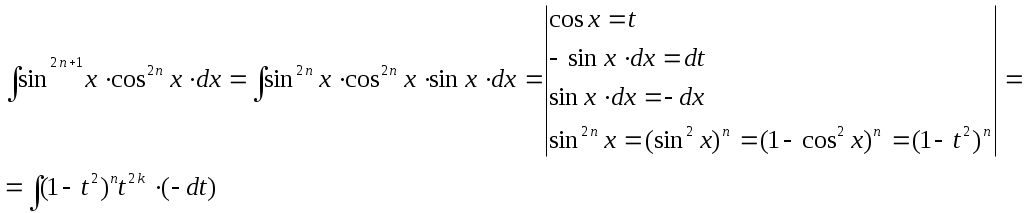
Интегрирование правильных рациональных дробей
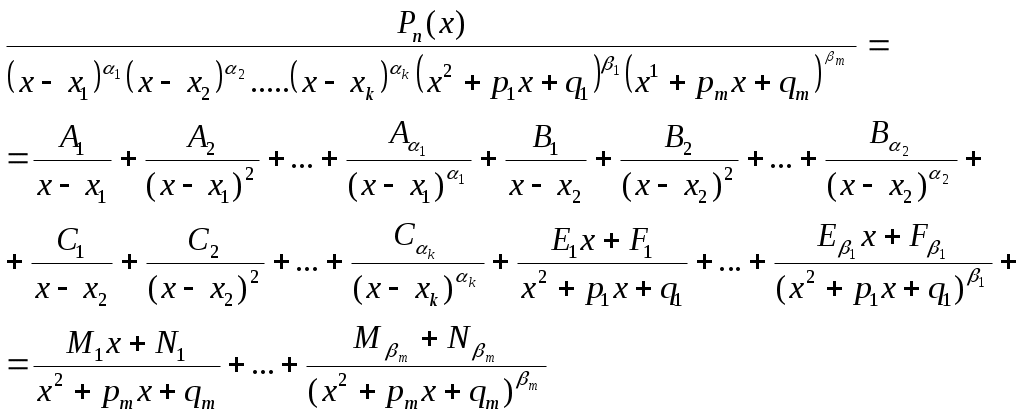Выделение полного квадрата:
Первый замечательный предел	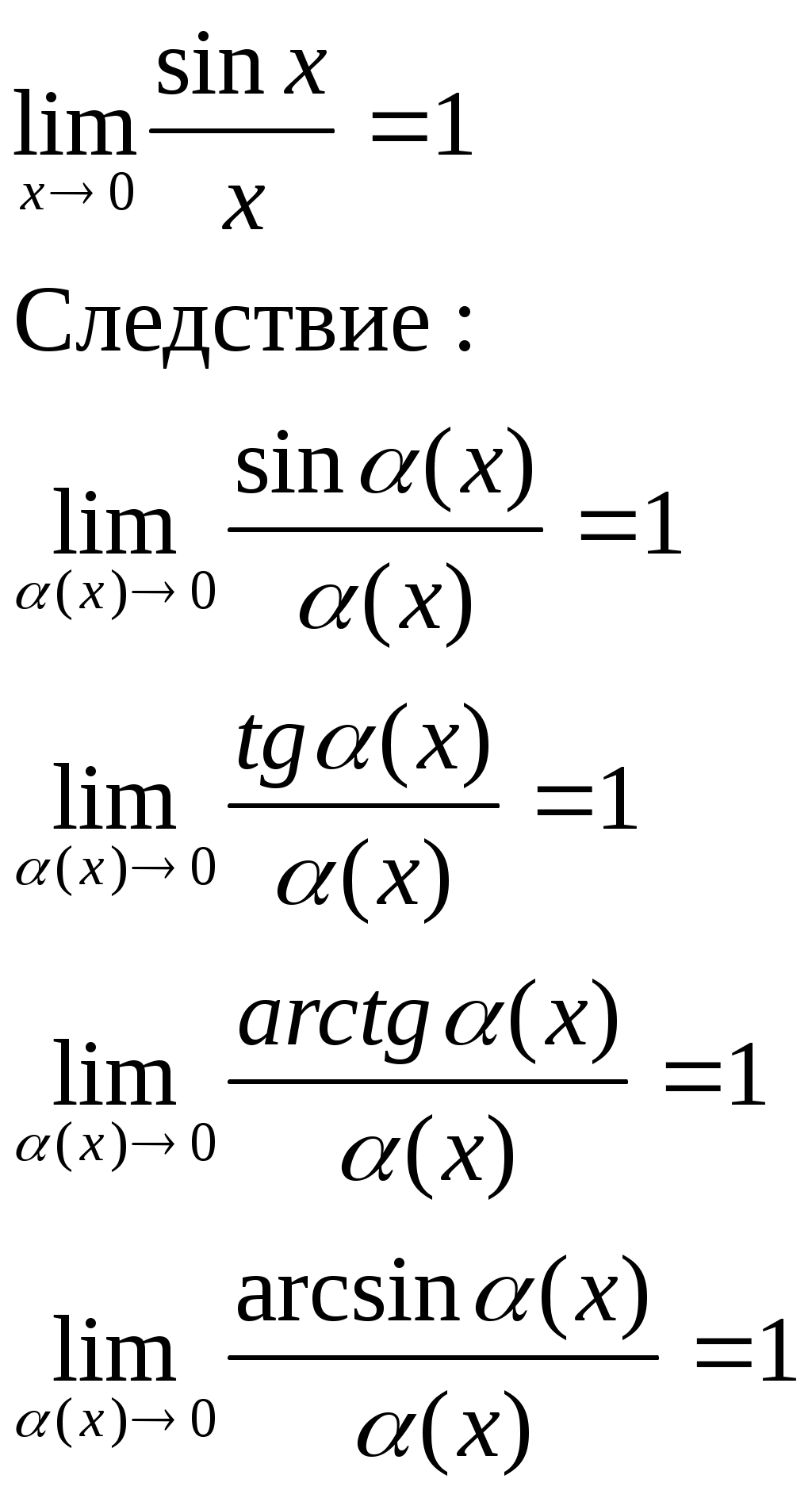			Второй замечательный предел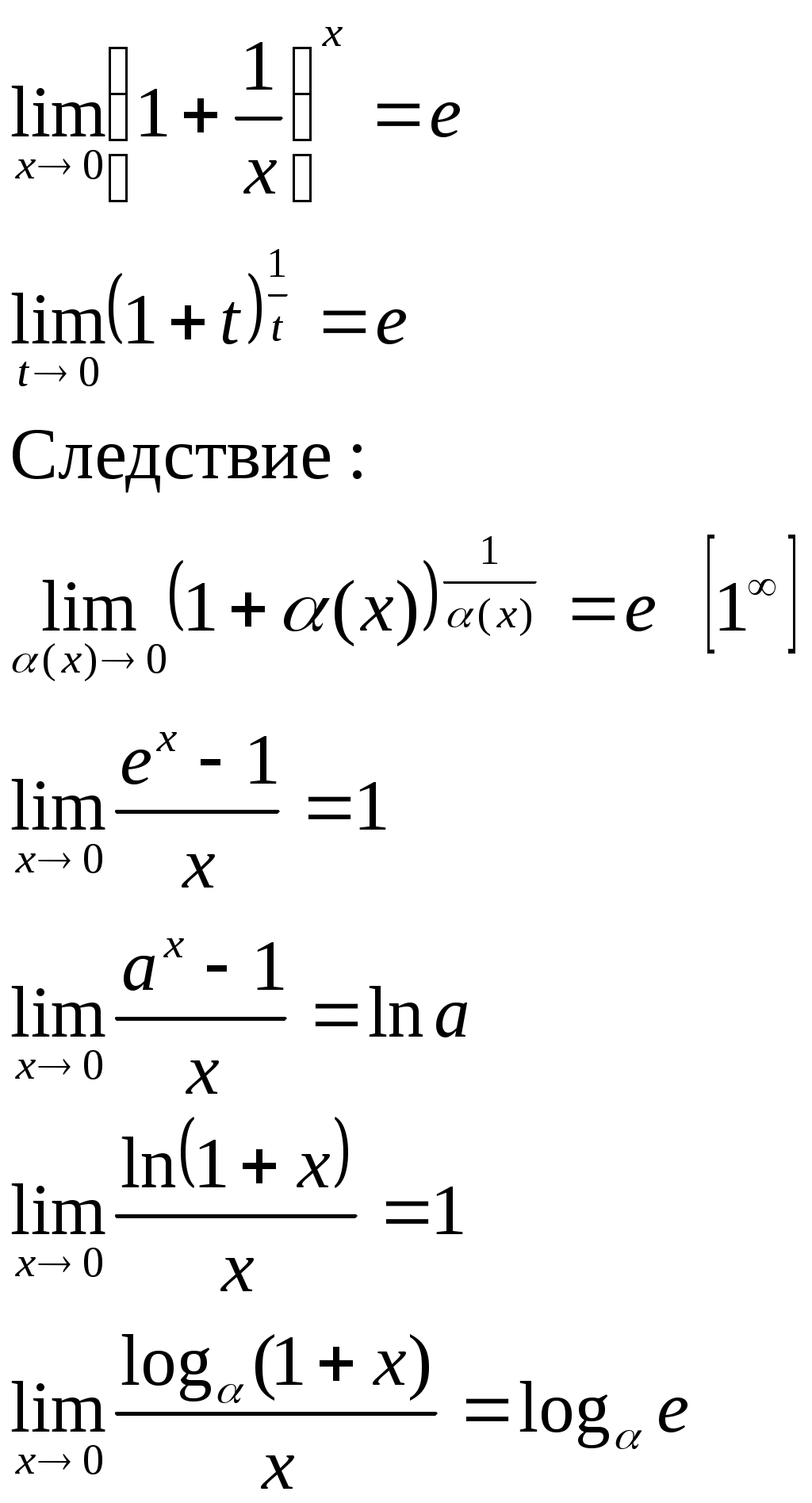
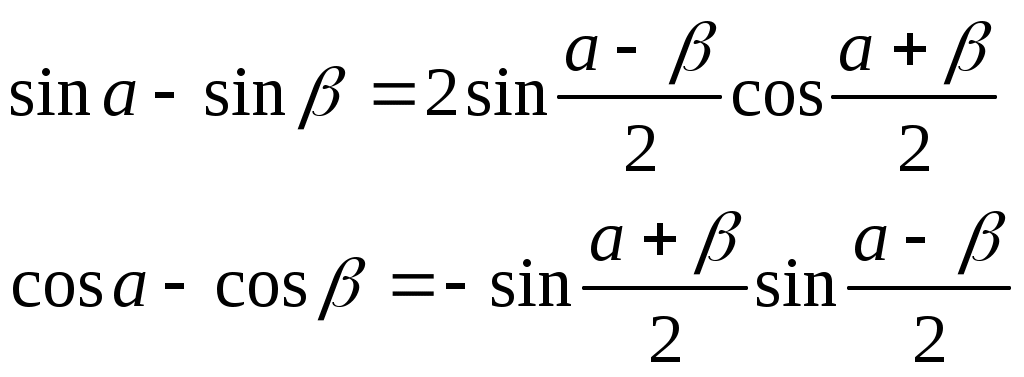Свойства преобразования Лапласа 1.Линейность 2.Теорема смещения 3.Теорема подобия 4.Теорема о дифференцировании изображения 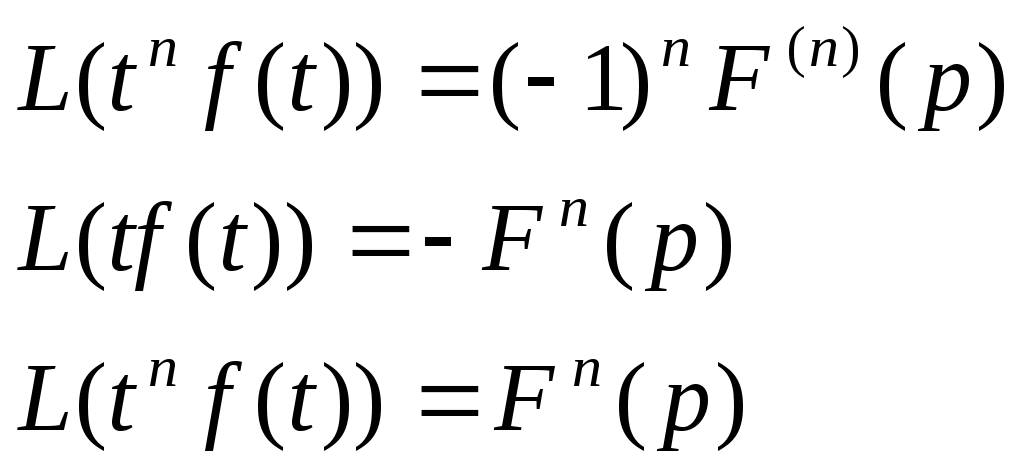5.Теорема о дифференцировании оригинала 6.Теорема о свертке 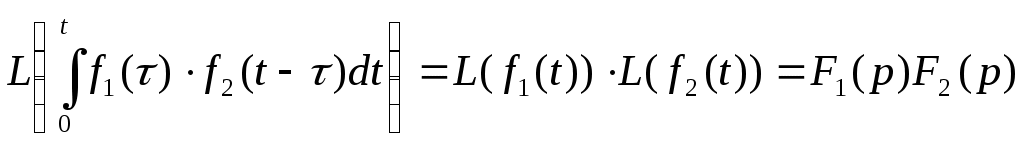7.Теорема запаздывания 8.Теорема об интегрировании оригинала 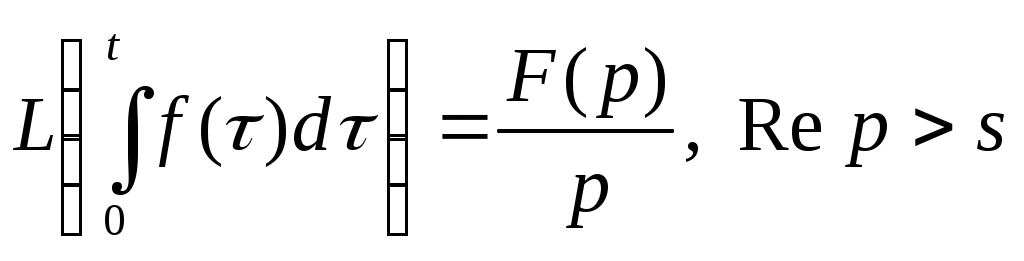9. Теорема об интегрировании изображения Если является оригиналом, то
	Таблица изображений и оригиналов преобразования Лапласа
	N	f(t)			F(p)
	1.
	2.
	3.
	4.
	5.
	6.
	7.
	8.
	9.
	10.
	11.
	12.
	13.
	14.
	15.
	16.
	17.
	18.
	19.
	20.

---

Свойства дискретного преобразования 1.Аддитивность 2.Однородность 3.Теорема смещения 4.Теорема запаздывания 5. Теорема опережения 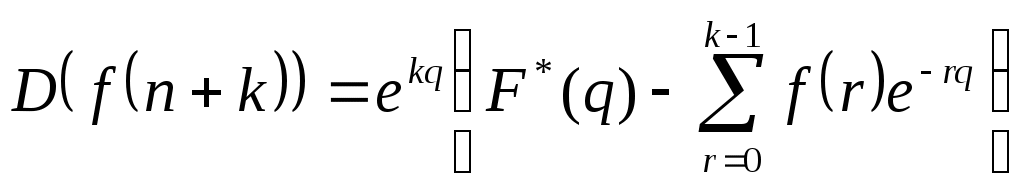6. Теорема о свертке 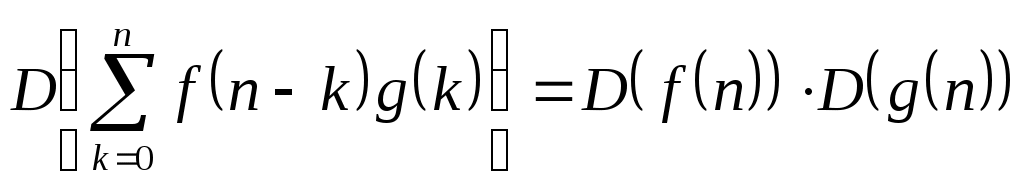7. Теорема о дифференцировании изображения 8. Теорема о дифференцировании по параметру: если , то 9. Теорема об интегрировании изображения: если , то 10.Изображение конечных сумм оригинала: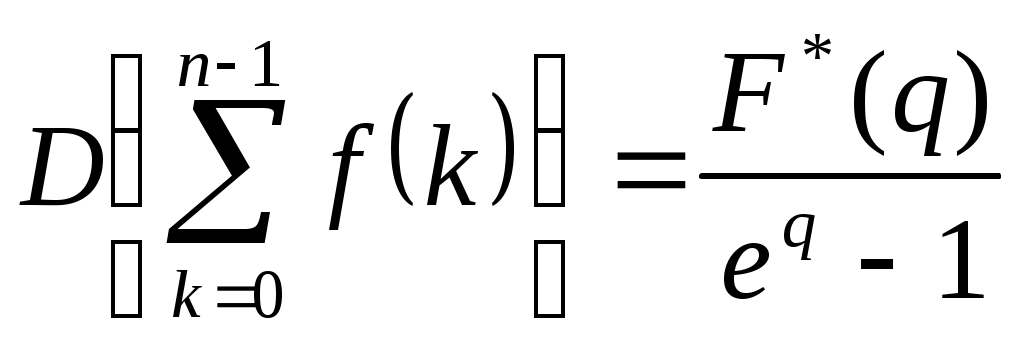

Свойства Z-преобразования 1.Аддитивность 2.Однородность 3.Теорема смещения 4.Теорема запаздывания 5. Теорема опережения 6. Теорема о свертке 7. Теорема о дифференцировании изображения 8. Теорема о дифференцировании по параметру: если , то 9.Изображение конечных сумм оригинала:

---

Таблица изображений и оригиналов дискретного преобразования Лапласа и Z-преобразования
N	f(n)	D(f(n))	Z(f(nT))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

---

Смотрите также файлы

• Лабораторная работа 1 Применение базовых средств пакета mathcad для решения нелинейных уравнений Казак И. А.docx

• Научнообразовательный журнал для студентов и преподавателей.docx

• Сабаты таырыбы Кестелі мліметтерді графикалы сынылуы.docx

• В данном докладе рассмотрена структура и сущностные характеристики познавательных универсальных учебных действий школьников, система заданий, формирующая познавательные ууд на уроках русского языка.docx

• Конспект занятия по фэмп Деление круга на четыре равные части.docx