Дисперсия:



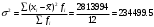
Среднеквадратичное отклонение:



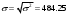
Среднее квадратическое отклонение свидетельствует о том, что рассматриваемая величина прожиточного минимума в среднем отклоняется от среднего найденного значения на 484,25 руб.

Коэффициент вариации v является критерием надежности средней, а также характеризует однородности совокупности. При v≤40% средняя является надежной и группировка однородна, при v≥40% - средняя не надежна.

Коэффициент вариации рассчитывается по формуле:



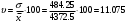
Коэффициент вариации меньше 40%, следовательно, средняя надежна и группировка однородна.

Вычислим моду и медиану:

Мода – наиболее часто встречающееся значение признака в совокупности.

Для интервального ряда распределения, сразу можно указать только интервал, где будут находиться мода и медиана.

Для определения их величины используют формулы:



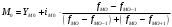
Исходные данные:

Интервалы	Кол-во элементов
1 интервал:	5
2 интервал:	2
3 интервал:	1
4 интервал:	4

Где:


Тогда:



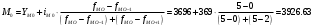
Получили, что наиболее часто величина прожиточного минимума приближалась к значению 3926,63.

Вычислим медиану.

Интервалы	Кол-во элементов	Накопленная частота
1 интервал:	5	5
2 интервал:	2	7
3 интервал:	1	8
4 интервал:	4	12

---

Медианным называется интервал, которому соответствует значение накопленной частоты большей полусуммы всех частот.



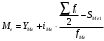
Где:


Подставим значения в формулу:



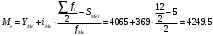
Получили, что половина исходных значений прожиточного минимума меньше найденного значения медианы, половин больше, чем 4249,5 руб.
По исходным данным о динамике прожиточного минимума Оренбургской области вычислили структурные средние и показатели вариации.

Рассмотрим показатели прожиточного минимума и вычислим абсолютные приросты базисным и цепным методом.

Базисные абсолютные приросты определяются при сравнении с переменной базой (базисный период), по формуле:



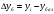
Цепные абсолютные приросты определяются при сравнении с переменной базой, по формуле:

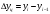
Базисные:

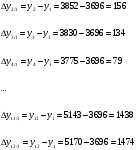Цепные: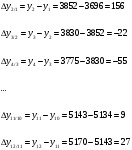

Относительные величины динамики принято называть темпами роста – темпами динамики (Т).

Базисные темпы роста - за основу принимается постоянная база сравнения, т.е. начальный уровень ряда динамики.

;

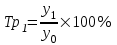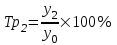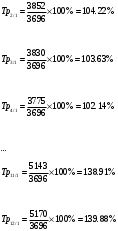Цепные темпы роста:

; ;

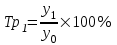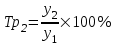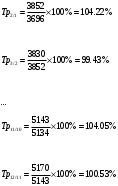Аналогично по остальным годам.

Результаты в таблице:

Таблица 2 – Числовые характеристики динамического ряда численности

Квартал	Величина прожиточного минимума	Абсолютные приросты	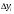	Темпы роста	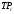		Темпы прироста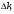
1	3696	Базисные	Цепные	Базисные	Цепные	4,22
2	3852	156	156	104,22	104,22	-0,57
3	3830	134	-22	103,63	99,43	-1,44
4	3775	79	-55	102,14	98,56	5,91
5	3998	302	223	108,17	105,91	6,03
6	4239	543	241	114,69	106,03	2,59
7	4349	653	110	117,67	102,59	2,71
8	4467	771	118	120,86	102,71	10,45
9	4934	1238	467	133,50	110,45	4,05
10	5134	1438	200	138,91	104,05	0,18
11	5143	1447	9	139,15	100,18	0,52
12	5170	1474	27	139,88	100,52	4,22

---

Темп прироста в рядах динамики характеризует относительную скорость изменения уровня ряда в единицу времени.


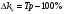
В нашем случае имеем темпы роста исходя из цепных темпов роста:


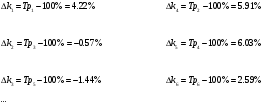
Определим средние показатели динамического ряда.

Среднеквартальный абсолютный прирост – характеризует среднюю скорость изменения уровня ряда в единицу времени и рассчитывается делением цепных абсолютных приростов на их число, т.е.

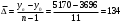руб.
Вывод: В рассмотренный период прожиточный минимум ежеквартально повышается в среднем на 134 руб.

Определим среднеквартальный темп роста.

Среднеквартальный темп роста рассчитывается по формуле средней геометрической из цепных темпов роста



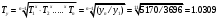
Определим среднегодовой темп прироста.



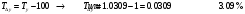
Вывод: За период прожиточный минимум ежеквартально возрастает на 3,09%Для наглядности изобразим ряд графически.

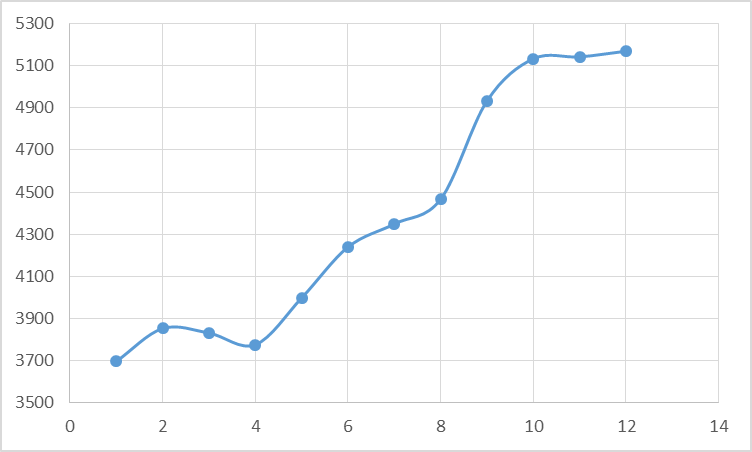
Имеем: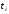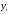
1	3696
2	3852
3	3830
4	3775
5	3998
6	4239
7	4349
8	4467
9	4934
10	5134
11	5143
12	5170

Произведем сглаживание ряда динамики. Для сглаживания можно применить метод скользящей средней. Применим, например, метод пятичленной скользящей средней.

---

Метод скользящей средней состоит в том, что исходный временной ряд преобразуется в ряд сглаженных значений (оценок).Применим формулы:



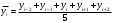
Затем проводится операция центрирования - повторном скольжении с шагом, равным двум.



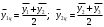
Таблица значений:

Прожиточный минимум, руб.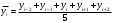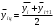
3696
3852
3830
3775	3830,2	3884,5
3998	3938,8	3988,5
4239	4038,2	4101,9
4349	4165,6	4281,5
4467	4397,4	4511
4934	4624,6	4715
5134	4805,4	4887,5
5143	4969,6
5170

Теперь для сглаженного ряда проще и точнее можно определить основную тенденцию (например, подобрать линию тренда). По полученным данным можем сделать вывод о наличии связи между рассматриваемым периодом и прожиточным минимумом.
Вынесем полученные данные на диаграмму:



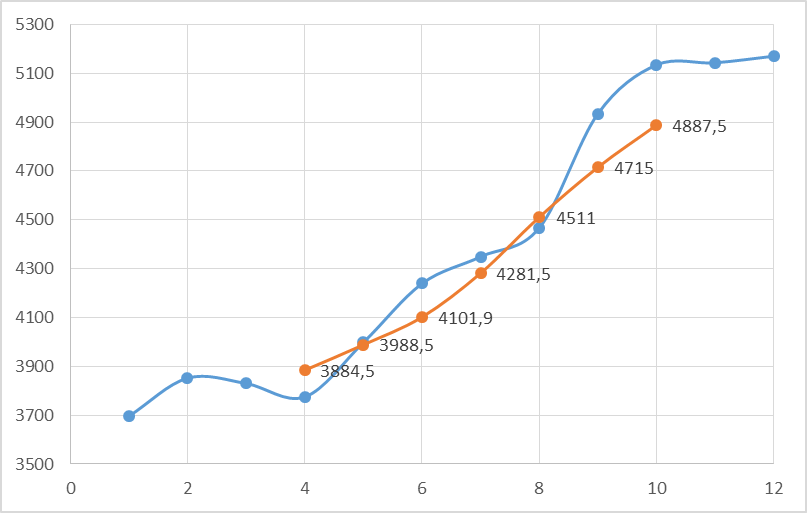
Рис.2. Пятичленное сглаживание

На графике отобразили исходный ряд и сглаженный.

По графику можем сделать вывод о росте величины прожиточного минимума во времени.

Уравнение регрессии будем искать в виде:

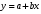
Рассчитаем выборочные коэффициенты корреляции. Для этого проведем промежуточные вычисления, по формулам и поместим результаты вычислений в таблицу:

---

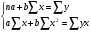
Найдем числовые значения сумм, заполнив вспомогательную расчетную таблицу.

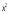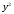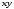1	3696	1	13660416	3696
2	3852	4	14837904	7704
3	3830	9	14668900	11490
4	3775	16	14250625	15100
5	3998	25	15984004	19990
6	4239	36	17969121	25434
7	4349	49	18913801	30443
8	4467	64	19954089	35736
9	4934	81	24344356	44406
10	5134	100	26357956	51340
11	5143	121	26450449	56573
12	5170	144	26728900	62040
78	52587	650	234120521,0	363952
6,50	4382,25	54,167	19510043,4	30329,33

---

Смотрите также файлы

• Согласовано с Утверждено на заседании.doc

• Разработка путевого плана для ограничивающего перегона.docx

• Практическая работа 24 Карстовые процессы. Цель изучить карстовые процессы. Краткие теоретические сведения.docx

• Цель занятия Овладение основами медицинских знаний и оказания первой помощи пострадавшим (ппп) при неотложных состояниях (травмах, отравлениях и различных видах поражений).docx

• Тема Морфологические нормы. Синтаксические нормы. Коммуникативные качества речи Задание Заполните предлагаемую ниже таблицу, включив в каждую графу не менее трех примеров речевых ошибок указанного типа..doc