Файл: Лабораторная работа 3 Решение слау по дисциплине Математическое моделирование процессов и систем.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 63
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Шаг 9.
Печать результатов: корни системы
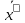 , число итераций k.
, число итераций k.Метод Зейделя
Реализация итерационного метода:
 | (17) |
Приведем к виду (из первого уравнений СЛАУ неизвестное выразим x1, из второго – x2, из последнего n-го уравнения – xn):
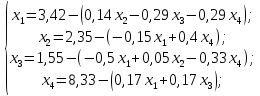 | (18) |
Вычислим первую итерацию, подставляя нулевые начальные условия в правые части уравнений. Затем полученные в левой части корни вновь подставим в правые части и таким образом вычислим первые 4 итерации:
Таблица 1 – расчет нескольких итераций
| k |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 3.4 | 2.3 | 1.5 | 8.3 |
| 2 | 5.9 | -0.1 | 7,3 | 6,1 |
| 3 | 6,9 | 1 | 6,9 | 5,9 |
| 4 | 6,99 | 0.99 | 6,99 | 6,002 |
Ответ:
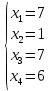 | (19) |
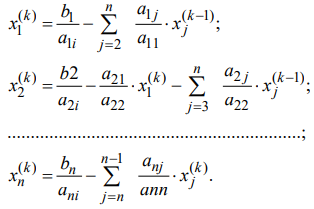 | (19) |

Оценка погрешности
| Прямые методы | |||||
| Метод | Аналитическое значение | значение программы | Абсолютная погрешность | Количество итераций | |
| Метод Гаусса | x0 = -2 x1 = 3 x2 = -3 x3 = -2 | x0 = -2 x1 = 3 x2 = -3 x3 = -2 | |x0- x0Pas|= 0 |x1- x1Pas|= 0 |x2- x2Pas|= 0 |x3- x3Pas|= 0 | - | |
| Итерационные методы | |||||
| МПИ | x0 = 7 x1 = 1 x2 = 7 x3 = 6 | x0 = 7.0004 x1 = 0.9999 x2 = 7.0005 x3 = 5.9998 | |x0- x0Pas|=0.0004 |x1- x1Pas|= 0.0001 |x2- x2Pas|= 0.0005 |x3- x3Pas|= 0.0002 | 10 | |
| Метод Зейделя | x0 = 7.0003 x1 = 1.0004 x2 = 6.9999 x3 = 5.9999 | |x0- x0Pas|=0.0007 |x1- x1Pas|=0.0006 |x2- x2Pas|=0.0001 |x3- x3Pas|=0.0001 | 7 | ||
| Метод Релаксации | ω =0.5 | x0 = 7.0003 x1 = 0.9997 x2 = 7.0014 x3 = 5.9991 | |x0- x0Pas|= 0.0007 |x1- x1Pas|=0.0003 |x2- x2Pas|=0.0086 |x3- x3Pas|= 0.0009 | 10 | |
| ω =1.5 | x0 = 7.0004 x1 = 0.9999 x2 = 7.0004 x3 = 5.9997 | |x0- x0Pas|= 0.0006 |x1- x1Pas|=0.0001 |x2- x2Pas|=0.0006 |x3- x3Pas|= 0.0003 | 13 | ||
Вывод:
Решили СЛАУ прямым и итерационным методом. Из итерационных методов наибольшая скорость сходимости у метода Зейделя, затем МПИ и нижних релаксаций (подвид метода Зейделя). Наименьшая абсолютная погрешность наблюдается при решении СЛАУ методом Зейделя.
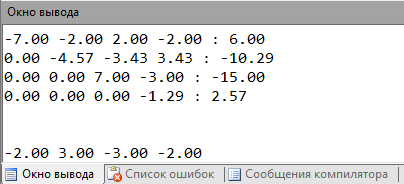
Метод Гаусса
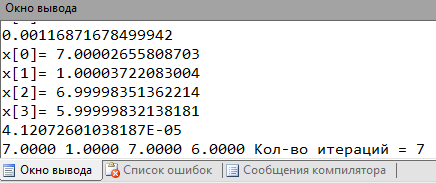
Метод Якоби
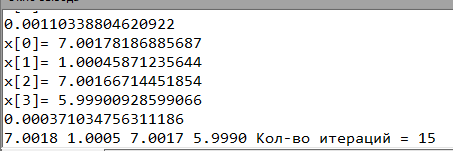
Метод Зейделя
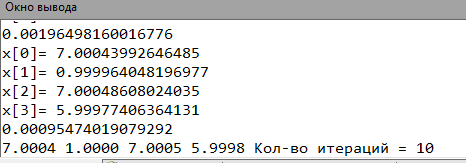
Нижняя релаксация (0.5)
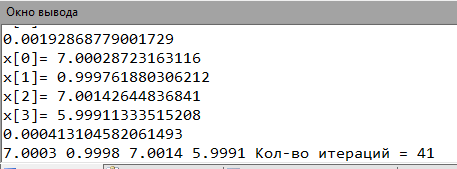
Верхняя релаксация (1.5)
Список используемой литературы
-
Теория и реализация задач вычислительной математики в пакете MathСad : учебное пособие / сост. А.И.Кочегуров, Е.А. Кочегурова; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2013. – 135 с.