Файл: Отчет по лабораторной работе 7 по дисциплине Компьютерные основы инфокоммуникационных технологий Тема работы Разработка алгоритмов основных структурных типов студента очного отделения 1 курса 12002210 группы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 04.02.2024

Просмотров: 46

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ФЕДЕРАЛЬНОЕ Государственное АВТОНОМНОЕ образовательное учреждение высшего образования

БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ

ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ

Отчет по лабораторной работе №7 по дисциплине: «Компьютерные основы инфокоммуникационных технологий»

Тема работы: «Разработка алгоритмов основных структурных типов»


студента очного отделения

1 курса 12002210 группы

Балабанов Андрей

Проверил:

Доцент

Трубицына Диана Игоревна

Белгород 2022

Цель работы:

Освоить методы построения и реализации алгоритмов.

Задачи работы:

  1. Изучить теоретический материал

  2. Выполнить задания для закрепления изученного материала

  3. Сделать вывод по проделанной работе

Выполнение лабораторной работы:

Задание №1

Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения получить A15 за пять операций, A21 за шесть операций и A28 за шесть операций.

  1. Начало;

  2. Ввод a;

  3. Вычислить A15 = a3 * a3 * a3 * a3 * a3;

  4. Вычислить A21 = a3 * a3 * a3 * a4 * a4 * a4;

  5. Вычислить A28 = a4 * a4 * a5 * a5 * a5 * a5;

  6. Вывод A15, A21, A28;

  7. Конец.



Задание №2

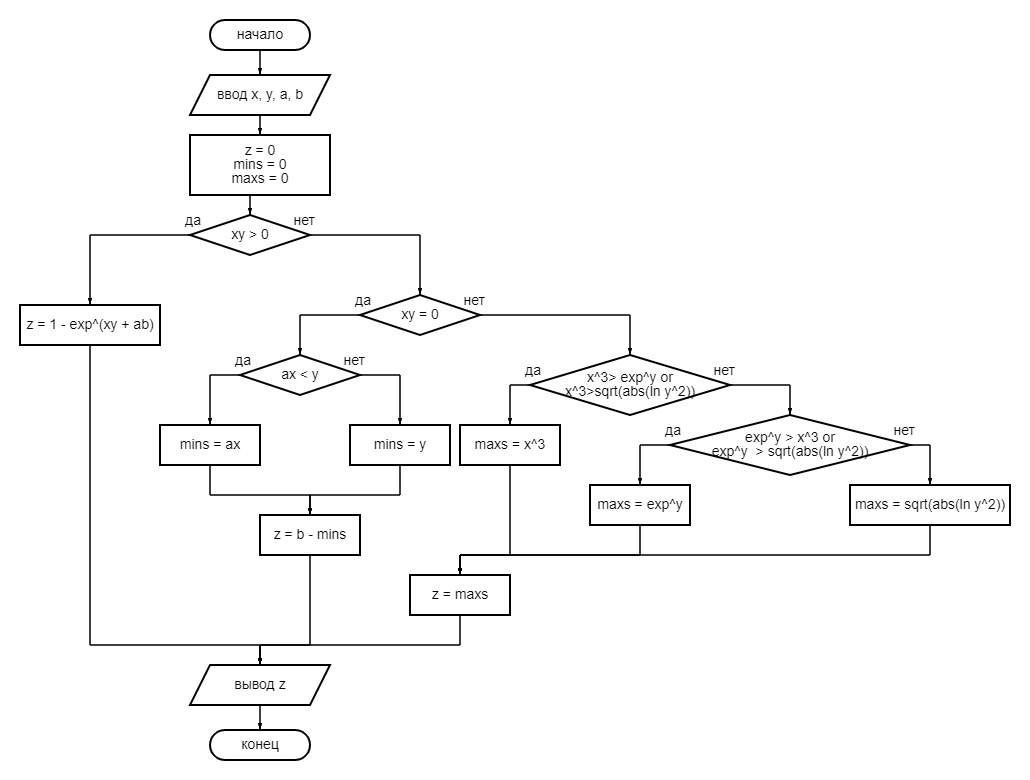
Z =




  1. Начало

  2. Ввод x, y, a, b

  3. z = 0, maxs = 0, mins = 0

  4. ЕСЛИ xy > 0,

ТО z = 1 – exp^(xy+ab)

  1. ЕСЛИ xy = 0,

ЕСЛИ ax < y,

ТО mins = ax,

ИНАЧЕ mins = y,

ТО z = b – mins

  1. ЕСЛИ xy < 0,

ЕСЛИ x^3 > exp^y or x^3 > sqrt(abs(ln y^2)),

ТО maxs = x^3,

ЕСЛИ exp^y > x^3 or exp^y > sqrt(abs(ln y^2)),

ТО maxs = exp^y,

ИНАЧЕ maxs = sqrt(abs(ln y^2)),

ТО z = maxs

  1. Вывод z

  2. Конец


Задание №3

Даны действительные числа x, y. Определить, принадлежит ли точка с координатами геометрической фигуре: четырехугольник с вершинами (0,1), (0.5,0), (0,-1), (-0.5,0).

  1. Начало

  2. Ввод x, y

  3. ЕСЛИ (x = 0 and y = 1) or (x = 0,5 and y = 0) or (x = 0 and y = -1) or (x = -0,5 and y = 0) or (x = 0 and y = 0,5) or (x = 0 and y = -0,5)

ТО вывод «точка принадлежит геометрической фигуре»

ИНАЧЕ «точка не принадлежит геометрической фигуре»

  1. Конец



Задание №4

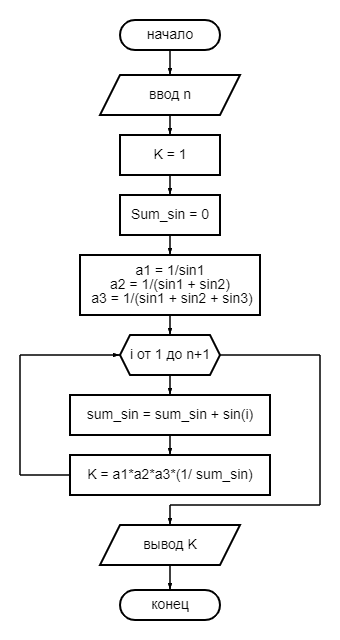
Дано натуральное N. Вычислить

1/sin1+1/(sin1+sin2) + 1/(sin1+sin2+sin3) + …+1 / (sin1+…+sinN).


  1. Начало

  2. Ввод n

  3. K = 1

  4. Sum_sin = 0, a1 = 1/sin1, a2 = 1/(sin1 + sin2), a3 = 1/(sin1 + sin2 + sin3)

  5. Цикл i от 1 до n + 1

  6. Вычислить sum_sin = sum_sin + sin(i),

K = a1*a2*a3*(1/ sum_sin)

  1. Вывод K

  2. Конец



Задание №5

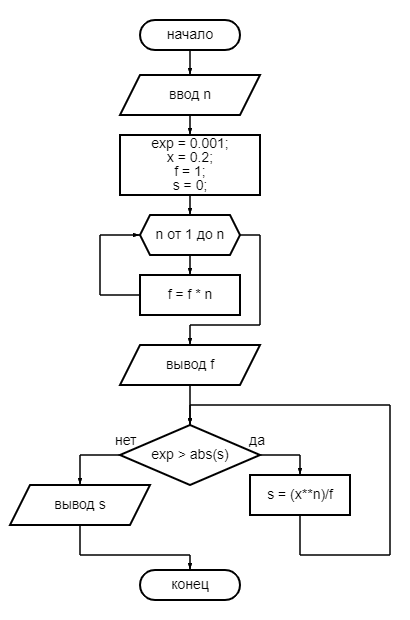
Вычислить и вывести те члены последовательности,  значения которых больше ε = 0.001 при x = 0.2.

  1. Начало;

  2. Ввод n;

  3. exp = 0.001, x = 0.2; f = 1; s = 0;

  4. Цикл n от 1 до n

Вычислить f = f * n;

  1. Вывод f

  2. До тех пор пока exp > abs(s)

Вычислить s = (x**n)/f;

  1. Вывод s;

  2. Конец.



Задание №6

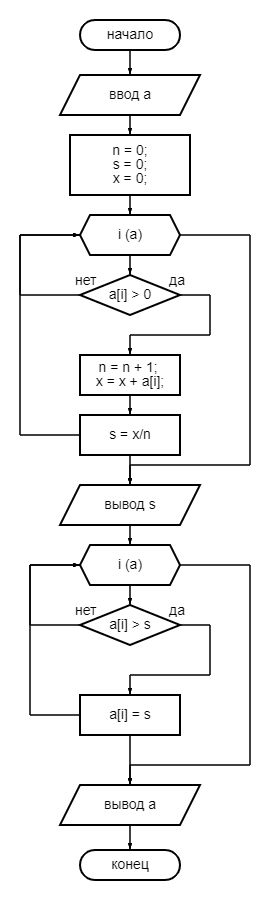
Ввести одномерный массив a = {5, -2, 0, 3, 4, 12, 7}. Вычислить и вывести среднее арифметическое значение положительных элементов массива и заменить этим значением те элементы массива, которые больше среднего арифметического.

  1. Начало;

  2. Ввод a;

  3. n = 0; s = 0; x = 0;

  4. Цикл i по a;

  5. ЕСЛИ a[i] > 0,

ТО n = n + 1; x = x + a[i];

  1. s = x/n;

  2. Вывод s;

  3. Цикл i по a;

  4. ЕСЛИ a[i] > s

ТО a[i] = s;

  1. Вывод a;

  2. Конец.



Задание №7

Дана целочисленная квадратная матрица порядка n. Определить, является ли она латинским квадратом: каждая строка и каждый столбец содержат числа 1, 2, …, n.



  1. Начало;

  2. Ввод n;

  3. a = [ ]

  4. b = True;

  5. Цикл i от 1 до n;

  6. Цикл j от 1 до n;

  7. a[i, j] - матрица размером n×n

  8. Вывод a;

  9. Цикл i от 1 до n;

  10. Цикл j от 1 до n;

  11. ЕСЛИ a[i, j] > n

ТО b = False;

  1. ЕСЛИ b = True

ТО вывод «Является»;

ИНАЧЕ «Не является»;

  1. Конец.

Вывод: в ходе выполнения лабораторной работы были изучены методы составления и реализации алгоритмов. Также был изучен графический способ описания алгоритма. Научились составлять словесный алгоритм и псевдокод для решения задач. Составили блок-схемы по данным алгоритмам и проверили их правильность.

Контрольные вопросы:

1.   Что такое алгоритм?

Алгоритм – описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи.

2.   Какими свойствами обладает алгоритм?

Алгоритм характеризуется следующими свойствами:

1)  дискретность (разрывность – противоположно непрерывности) – свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, «делится на шаги»;

2)  массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных;

3)  определенность (детерминированность, точность) – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов;

4)  результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное число шагов.

5)  формальность – это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекает от содержания поставленной задачи и лишь строго выполняет инструкции.

3.   Что из себя представляет алгоритмический язык?

Алгоритм моделирует решение задачи в виде точно определенной последовательности действий для некоторого исполнителя по преобразованию исходных данных в результирующие.

Для его описания используется алгоритмический язык – набор символов и правил образования и истолкования конструкций из этих символов для записи алгоритмов.

4.   Какие существуют изобразительные средства алгоритмов?


Основными изобразительными средствами алгоритмов являются следующие способы их записи:

    словесный;

    формульно-словесный;

    графический;

    псевдокод;

    табличный;

    операторный.

5.   Что из себя представляет графический способ описания алгоритма?

Графический способ получил наибольшее распространение. В этом способе алгоритм представляется в виде схемы, состоящей из элементов символов, отражающих отдельные операции технологического процесса обработки данных и отдельные вычислительные операции.

Каждый этап процесса переработки данных представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций 

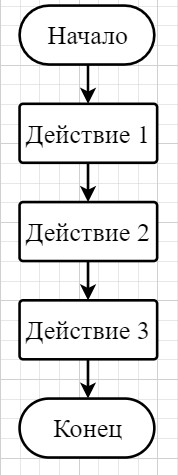
6.   Опишите линейную алгоритмическую структуру

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.



7.   Опишите алгоритмическую структуру «разветвление»

Структура «Разветвление»

Данная структура применяется, когда в зависимости от заданного условия нужно выполнить либо одно, либо другое действие.



Проверка «Условие?» представляется предикатом, т.е. функцией, задающей логическое выражение или условие, значением которого может быть истина («+») или ложь («-»). Эта структура может быть неполной, когда отсутствует действие, выполняемое при ложном (или истинном) значении логического выражения.



8.   Опишите алгоритмическую структуру «цикл»

В алгоритмическую структуру цикл входит серия команд, выполняемая многократно. Такая последовательность команд называется телом цикла.

В алгоритмической структуре цикл серия команд (тело цикла) выполняется многократно.

Циклические алгоритмические структуры бывают двух типов:


• циклы со счётчиком, в которых тело цикла выполняется определённое количество раз;
• циклы по условию, в которых тело цикла выполняется, пока истинно (или ложно) заданное условие.

Алгоритмическая структура цикл может быть описана графически с помощью блок-схемы.



Цикл со счётчиком используется, когда заранее известно, какое количество повторений тела цикла необходимо выполнить. Количество повторений задаётся с помощью счётчика.

Цикл с условием используется, когда заранее неизвестно, какое количество раз должно повториться тело цикла. В таких случаях количество повторений зависит от некоторого условия.

Цикл называется циклом с предусловием, если условие выхода из цикла стоит в начале, перед телом цикла. В случае ложности условия цикл с предусловием не выполнится ни разу.

Цикл называется циклом с постусловием, если условие выхода из цикла стоит в конце, после тела цикла. Цикл с постусловием выполняется обязательно, как минимум один раз, независимо от того, истинно условие или нет.

9.   Какие виды циклов вы знаете?

  • безусловный цикл

Безусловные циклы – это циклы, которые выполняются бесконечно. Пример, «пока 1 = 1, напечатать 1 = 1». Такая программа будет выполняться пока её не прервут вручную.

  • цикл с предусловием

Цикл с предусловием – это цикл, который выполняется, пока истинно некоторое условие, указанное перед его началом. Это условие проверяется до выполнения тела цикла, поэтому тело может быть не выполнено ни разу (если условие с самого начала ложно). В большинстве процедурных языков программирования реализуется оператором while, отсюда его второе название – while – цикл.



  • цикл с постусловием

Цикл с постусловием – цикл, в котором условие проверяется после выполнения тела цикла. Отсюда следует, что тело всегда выполняется хотя бы один раз.

  • цикл со счётчиком

Цикл со счётчиком – цикл, в котором некоторая переменная изменяет своё значение от заданного начального значения до конечного значения с некоторым шагом, и для каждого значения этой переменной тело цикла выполняется один раз.

  • цикл с выходом из середины

Цикл с выходом из середины – это цикл, в котором есть команды, нарушающие порядок выполнения конструкций цикла. Существует команда досрочного выхода из цикла – break и команда пропуска итерации – continue. Это команды служат для управления работой цикла.

Смотрите также файлы