ПОКАЗАТЕЛИ ВАРИАЦИИ ИНТЕРВАЛЬНОГО РЯДА

ЧИСЛА ПАДЕНИЯ КУКУРУЗНОЙ МУКИ ТОНКОГО ПОМОЛА
Мука кукурузная тонкого помола.

Таблица для расчета показателей.

Группы	Середина интервала, xцентр	Кол-во, fi	xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi	Относительная частота, fi/f
332 - 335	333.5	3	1000.5	3	21.375	152.297	0.15
336 - 340	338	6	2028	9	15.75	41.344	0.3
341 - 343	342	7	2394	16	9.625	13.234	0.35
344 - 347	345.5	2	691	18	9.75	47.531	0.1
348 - 351	349.5	2	699	20	17.75	157.531	0.1
Итого		20	6812.5		74.25	411.938	1

Для оценки ряда распределения найдем следующие показатели:

Показатели центра распределения.

---

Средняя взвешенная (выборочная средняя)

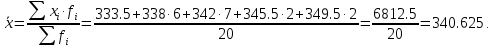
Мода. Мода ‒ наиболее часто встречающееся значение признака у единиц данной совокупности.

,
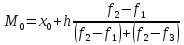где x₀ – начало модального интервала;

h – величина интервала;

f₂ –частота, соответствующая модальному интервалу;

f₁ – предмодальная частота;

f₃ – послемодальная частота.
Выбираем в качестве начала интервала 488, так как именно на этот интервал приходится наибольшее количество.

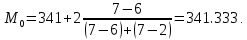
Наиболее часто встречающееся значение ряда – 341.333.
Медиана. Медиана делит выборку на две части: половина вариант меньше медианы, половина ‒ больше.

Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии «выбросов» данных, медиана более устойчива к воздействию отклоняющихся данных.

В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда.

Медианным является интервал 341-343, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
,


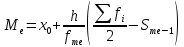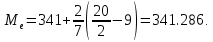
Таким образом, 50 % единиц совокупности будут меньше по величине .

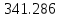В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (x_ср = M_e = M_o), а в умеренно асимметричных они соотносятся таким образом: 3(x_ср‒M_e) ≈ x_ср‒M

---

_o
Квартили.

Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25 % единиц совокупности будут меньше по величине Q₁, 25 % будут заключены между Q₁ и Q₂, 25 % ‒ между Q₂ и Q₃. Остальные 25 % превосходят Q₃.
,

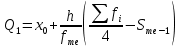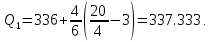
Таким образом, 25 % единиц совокупности будут меньше по величине 337.333 Q₂ совпадает с медианой, Q₂ = 341.286.
,


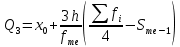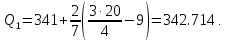
Остальные 25 % превосходят значение 342.714.
Квартильный коэффициент дифференциации.
k = Q₁ / Q₃.
k = 337.333 / 342.714 = 0,98.
Децили (децентили). Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10 % единиц совокупности будут меньше по величине D₁; 80 % будут заключены между D₁ и D₉; остальные 10 % превосходят D₉.
,

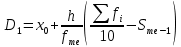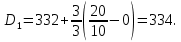
Таким образом, 10 % единиц совокупности будут меньше по величине 334.

,

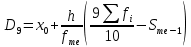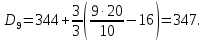
Остальные 10 % превосходят 347.
Среднее значение изучаемого признака по способу моментов.



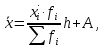
где А – условный нуль, равный варианте с максимальной частотой (середина

интервала с максимальной частотой);

h – шаг интервала.


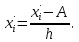
Находим А = 501

---

, шаг интервала h = 26.
Средний квадрат отклонений по способу моментов.




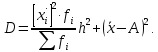
Таблица

Расчет квадрата отклонений по способу моментов

xц	x*i	x*ifi	[x*i]2fi
333.5	-2.8333333333333	-8.5	24.083333333333
338	-1.3333333333333	-8	10.666666666667
342	0	0	0
345.5	1.1666666666667	2.3333333333333	2.7222222222222
349.5	2.5	5	12.5
		-9.1666666666667	49.972222222222

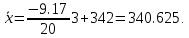
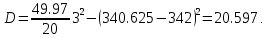
Среднее квадратическое отклонение.


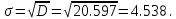
Показатели вариации.

Абсолютные показатели вариации.

Размах вариации ‒ разность между максимальным и минимальным значениями признака первичного ряда.
R = x_max ‒ x_min = 351 ‒ 332 = 19.
Среднее линейное отклонение вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.


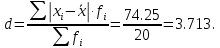
Каждое значение ряда отличается от другого в среднем на 3.713.

Дисперсия характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

---

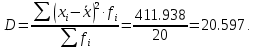
Несмещенная оценка дисперсии ‒ состоятельная оценка дисперсии (исправленная дисперсия).

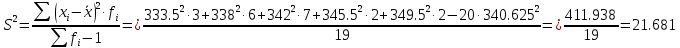
Среднее квадратическое отклонение.


Каждое значение ряда отличается от среднего значения 340.625 в среднем на 4.538.
Оценка среднеквадратического отклонения.

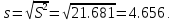
Относительные показатели вариации.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.

Коэффициент вариации ‒ мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

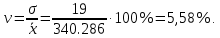
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.

Линейный коэффициент вариации или Относительное линейное отклонение характеризует долю усредненного значения признака абсолютных отклонений от средней величины.



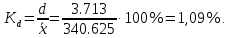
Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.




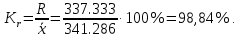
Показатели формы распределения.

Относительный показатель квартильной вариации


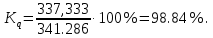
Степень асимметрии. Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии.
As = M₃/s³,


где

---

Смотрите также файлы

• Кейс Техсервис Планетаавто.docx

• Крым или Турция, где лучше отдохнуть.docx

• Факультет Экономика и управление.docx

• ПН аза тілі блім Табиат жне экология.docx

• Самостоятельная работа создание своего персонажа.docx