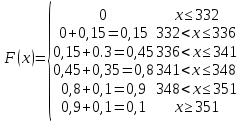Файл: Показатели вариации интервального ряда числа падения кукурузной муки тонкого помола.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 35
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
M3 ‒ центральный момент третьего порядка.
s ‒ среднеквадратическое отклонение.
M3 = 454.36/100 = 22.72.
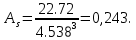
Положительная величина указывает на наличие правосторонней асимметрии. Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии:
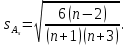
Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Расчет центральных моментов проводим в аналитической таблице.
Расчет центральных моментов проводим в аналитической таблице:
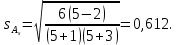
В анализируемом ряду распределения наблюдается несущественная асимметрия (0,243/0,612 = 0,4 < 3).
Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона:
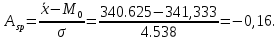
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя:
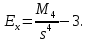
Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) ‒ отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3.
M4 = 21579.01/20 = 1078.95.
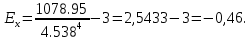
Число 3 вычитается из отношения μ4/σ4 потому, что для нормального закона распределения μ4/σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные ‒ отрицательным эксцессом.
Ex < 0 ‒ плосковершинное распределение. Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx, где sEx ‒ средняя квадратическая ошибка коэффициента эксцесса.
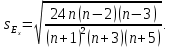
Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным.
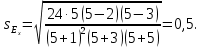
Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным.
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.
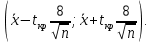
Определяем значение tkp по таблице распределения Стьюдента. По таблице Стьюдента находим: Tтабл (n‒1; α/2) = Tтабл (19; 0,025) = 2,433.
Стандартная ошибка выборки для среднего:
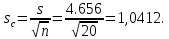
Стандартная ошибка среднего указывает, на сколько среднее выборки 340,625 отличается от среднего генеральной совокупности.
Предельная ошибка выборки равна:
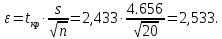
или ε = tkp sc = 2,433×1.041 = 2,533.
Доверительный интервал: (340.625 - 2.533;340.625 + 2.533) = (338.092;343.158).
С вероятностью 0,95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(X2n-1 < hH) = (1-γ)/2 = (1-0.954)/2 = 0.023.
Для количества степеней свободы k = 19 по таблице распределения χ2 находим: X2(19;0.023) = 11.65091.
Случайная ошибка дисперсии нижней границы:
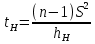
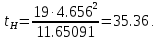
Вероятность выхода за верхнюю границу равна P(X2n-1 ≥ hB) = 1 - P(X2n-1 < hH) = 1 - 0.023 = 0.977.
Для количества степеней свободы k = 19, по таблице распределения X2 находим:
X2(19;0.977) = 11.65091.
Случайная ошибка дисперсии верхней границы:
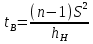
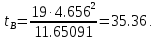
Таким образом, интервал (35.36;35.36) покрывает параметр S2 с надежностью γ = 0.954
Доверительный интервал для среднеквадратического отклонения.
S(1-q) < σ < S(1+q)
Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 20
По таблице q=q(γ ; n) определяем параметр q(0.954;20) =4.656(1-) < σ < 4.656(1+)
4.656 < σ < 4.656
Таким образом, интервал (4.656;4.656) покрывает параметр σ с надежностью γ = 0.954
Интервальное оценивание генеральной доли (вероятности события).
Доверительный интервал для генеральной доли (p· ‒ ε; p· + ε)
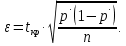
В этом случае 2Ф(tkp) = γ. Ф(tkp) = γ/2 = 0,954/2 = 0,477.
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0,477
tkp(γ) = (0,477) = 2.
Таблица
Интервальное оценивание генеральной доли
С вероятностью 0,954 при большем объеме выборке эти доли будут находиться в заданных интервалах.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью показателей As и Ex.
В случае нормального распределения справедливо следующее условие:
|As| < 3SAs; |A| < 3SAs; |E| < 3SEx .
Проверим выполнение этого условия для нашего примера.
SAs=0.6124, SEx=0.5
As=0.243, Ex=-0.46
|0.243| < 3
0.6124=1.8371
|-0.46| < 3 0.5=1.5
Условия выполняются.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью правила 3-х сигм. Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал:
(x̅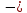
3 · σ; x̅ + 3 · σ)
В нашем случае этот интервал составит: (340.625-3·4.538;340.625-3·4.538) = (327.011;354.239)
Все значения величин попадают в интервал, так как xmin=332; xmax=351
Выводы:
Каждое значение ряда отличается от среднего значения 340.625 в среднем на 4.538.
Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.
Поскольку коэффициент вариации меньше 30%, то совокупность однородна. Полученным результатам можно доверять. Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.
Функция распределения F(X).
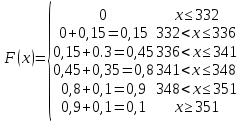
s ‒ среднеквадратическое отклонение.
M3 = 454.36/100 = 22.72.
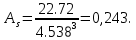
Положительная величина указывает на наличие правосторонней асимметрии. Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии:
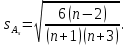
Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Расчет центральных моментов проводим в аналитической таблице.
Расчет центральных моментов проводим в аналитической таблице:
| Группы | Середина интервала, xцентр | Кол-во, fi | (x-xср)3·fi | (x-xср)4·fi |
| 332 - 335 | 333.5 | 3 | -1085.115 | 7731.446 |
| 336 - 340 | 338 | 6 | -108.527 | 284.884 |
| 341 - 343 | 342 | 7 | 18.197 | 25.021 |
| 344 - 347 | 345.5 | 2 | 231.715 | 1129.61 |
| 348 - 351 | 349.5 | 2 | 1398.09 | 12408.047 |
| Итого | | 20 | 454.359 | 21579.009 |
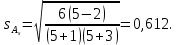
В анализируемом ряду распределения наблюдается несущественная асимметрия (0,243/0,612 = 0,4 < 3).
Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона:
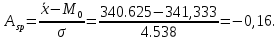
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя:
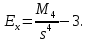
Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) ‒ отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3.
M4 = 21579.01/20 = 1078.95.
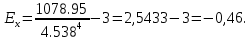
Число 3 вычитается из отношения μ4/σ4 потому, что для нормального закона распределения μ4/σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные ‒ отрицательным эксцессом.
Ex < 0 ‒ плосковершинное распределение. Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx, где sEx ‒ средняя квадратическая ошибка коэффициента эксцесса.
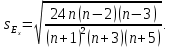
Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным.
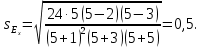
Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным.
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.
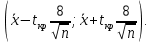
Определяем значение tkp по таблице распределения Стьюдента. По таблице Стьюдента находим: Tтабл (n‒1; α/2) = Tтабл (19; 0,025) = 2,433.
Стандартная ошибка выборки для среднего:
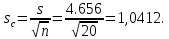
Стандартная ошибка среднего указывает, на сколько среднее выборки 340,625 отличается от среднего генеральной совокупности.
Предельная ошибка выборки равна:
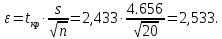
или ε = tkp sc = 2,433×1.041 = 2,533.
Доверительный интервал: (340.625 - 2.533;340.625 + 2.533) = (338.092;343.158).
С вероятностью 0,95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(X2n-1 < hH) = (1-γ)/2 = (1-0.954)/2 = 0.023.
Для количества степеней свободы k = 19 по таблице распределения χ2 находим: X2(19;0.023) = 11.65091.
Случайная ошибка дисперсии нижней границы:
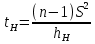
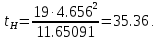
Вероятность выхода за верхнюю границу равна P(X2n-1 ≥ hB) = 1 - P(X2n-1 < hH) = 1 - 0.023 = 0.977.
Для количества степеней свободы k = 19, по таблице распределения X2 находим:
X2(19;0.977) = 11.65091.
Случайная ошибка дисперсии верхней границы:
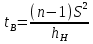
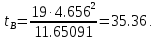
Таким образом, интервал (35.36;35.36) покрывает параметр S2 с надежностью γ = 0.954
Доверительный интервал для среднеквадратического отклонения.
S(1-q) < σ < S(1+q)
Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 20
По таблице q=q(γ ; n) определяем параметр q(0.954;20) =4.656(1-) < σ < 4.656(1+)
4.656 < σ < 4.656
Таким образом, интервал (4.656;4.656) покрывает параметр σ с надежностью γ = 0.954
Интервальное оценивание генеральной доли (вероятности события).
Доверительный интервал для генеральной доли (p· ‒ ε; p· + ε)
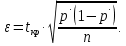
В этом случае 2Ф(tkp) = γ. Ф(tkp) = γ/2 = 0,954/2 = 0,477.
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0,477
tkp(γ) = (0,477) = 2.
Таблица
Интервальное оценивание генеральной доли
| Доля i-ой группы fi / ∑f | Средняя ошибка выборки для генеральной доли, ε | Нижняя граница доли, p· ‒ ε | Верхняя граница доли, p· + ε |
| 0.15 | 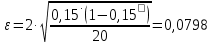 | 0.0702 | 0.23 |
| 0.3 | 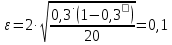 | 0.198 | 0.402 |
| 0.35 | 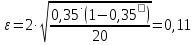 | 0.243 | 0.457 |
| 0.1 | 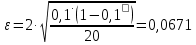 | 0.0329 | 0.167 |
| 0.1 | 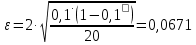| 0.0329 | 0.167 |
С вероятностью 0,954 при большем объеме выборке эти доли будут находиться в заданных интервалах.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью показателей As и Ex.
В случае нормального распределения справедливо следующее условие:
|As| < 3SAs; |A| < 3SAs; |E| < 3SEx .
Проверим выполнение этого условия для нашего примера.
SAs=0.6124, SEx=0.5
As=0.243, Ex=-0.46
|0.243| < 3
0.6124=1.8371|-0.46| < 3
0.5=1.5Условия выполняются.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью правила 3-х сигм. Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал:
(x̅
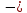3 · σ; x̅ + 3 · σ)В нашем случае этот интервал составит: (340.625-3·4.538;340.625-3·4.538) = (327.011;354.239)
Все значения величин попадают в интервал, так как xmin=332; xmax=351
Выводы:
Каждое значение ряда отличается от среднего значения 340.625 в среднем на 4.538.
Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.
Поскольку коэффициент вариации меньше 30%, то совокупность однородна. Полученным результатам можно доверять. Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.
Функция распределения F(X).