ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 285
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Отношения между классами
Кроме внутреннего устройства или структуры классов, на диаграмме классов необходимо отобразить различные отношения между ними. Основными отношениями или связями в языке UML являются:
-
отношение зависимости (dependency relationship); -
отношение ассоциации (association relationship): -
отношение обобщения (generalization relationship); -
отношение реализации (realization relationship).
Все эти отношения обозначаются по-своему на диаграмме и отражают различные типы взаимосвязей между классами и их объектами.
Отношение зависимости
Отношение зависимости используется в ситуации, когда не которое изменение одного элемента модели может потребовать изменения другого зависимого от него элемента модели.
Отношение зависимости графически изображается пунктир ной линией между соответствующими элементами со стрелкой на одном из ее концов («>» или ««-»). На диаграмме классов данное отношение связывает отдельные классы между собой, при этом стрелка направлена от класса-клиента зависимости к независимому классу или классу-источнику (рисунок 4.2). На дан ном рисунке изображены два класса: Класс А и Класс Б, при этом Класс Б является источником некоторой зависимости, а Класс_А — клиентом этой зависимости.
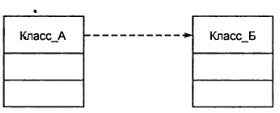
Рисунок 4.2 – Графическое изображение отношения зависимости на диаграмме классов
Отношение ассоциации
Отношение ассоциации обозначается сплошной линией с дополнительными специальными символами, которые характеризуют отдельные свойства конкретной ассоциации. Это могут быть имя ассоциации, а также имена и кратность классов-ролей ассоциации. Имя ассоциации является необязательным, но если оно задано, то записывается с прописной (заглавной) буквы рядом с линией соответствующей ассоциации.
Ассоциация, связывающая два класса (или класс с самим со бой), называется бинарной. Для бинарной ассоциации на диаграмме может быть указан порядок следования классов с использованием треугольника в форме стрелки рядом с именем данной ассоциации. Направление этой стрелки указывает на по рядок классов, один из которых является первым (со стороны основания треугольника), а другой – вторым (со стороны вер шины треугольника). Отсутствие данной стрелки рядом с именем ассоциации означает, что порядок следования классов в рассматриваемом отношении не определен.
На рисунке 4.3 показано отношение бинарной ассоциации между классом «Группа» и классом «Студент». Они связаны между собой бинарной ассоциацией «Учеба», имя которой указано на рисунке над линией ассоциации. Порядок следования классов в данном отношении таков: первым является класс «Студент», а вторым – класс «Группа».
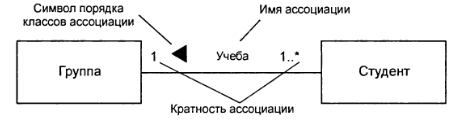
Рисунок 4.3 – Графическое изображение отношения бинарной ассоциации между классами
Можно, хотя это редко бывает необходимо, создавать ассоциации, связывающие сразу несколько классов; они называются N-арными. N-арная ассоциация графически обозначается ромбом, от которого к символам классов данной ассоциации ведут линии. В этом случае ромб соединяется с символами соответствующих классов сплошными линиями. Имя N-арной ассоциации записывается рядом с ромбом соответствующей ассоциации.
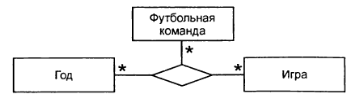
Рисунок 4.4 –Графическое изображение тернарной ассоциации
Пример тернарной ассоциации показан на рисунке 4.4. Здесь изображено отношение между тремя классами: «Футбольная команда», «Год» и «Игра», которое может представлять информацию об играх футбольных команд в национальном чемпионате в течение нескольких последних лет.
Наиболее важные свойства ассоциации указываются на диаграмме рядом с этими элементами ассоциации и должны перемещаться вместе с ними.
К таким свойствам относятся:
-
имя роли отдельного класса, входящего в ассоциацию, представляет собой строку текста рядом с концом ассоциации для соответствующего класса. Имя роли не является обязательным элементом обозначений и может отсутствовать на диаграмме; -
кратность отдельных классов, являющихся концами ассоциации. Интервал кратности записывается рядом с концом ассоциации и для N-арной ассоциации означает потенциальное число отдельных экземпляров или значений кортежей этой ассоциации, которые могут иметь место, когда остальные N- 1 экземпляров или значений классов фиксированы.
В рассмотренном ранее примере (рисунок 4.2) кратность «l» для класса «Группа» означает, что каждый студент может учиться только в одной группе. Кратность «1..*» для класса «Студент» означает, что в каждой группе могут учиться несколько студентов, общее число которых заранее неизвестно и ничем не ограничено, но всегда больше нуля.
На диаграмме классов может присутствовать так называемая исключающая ассоциация (Xor-association). Она означает, что из нескольких потенциально возможных вариантов данной ассоциации в каждый момент времени может использоваться только один ее экземпляр. Исключающая ассоциация изображается пунктирной линией, соединяющей две ассоциации и более, рядом с которой записывается строка-ограничение {хог}.
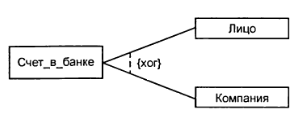
Рисунок 4.5 – Графическое изображение исключающей ассоциации между тремя классами
Например, счет в банке может быть открыт для клиента, в качестве которого может выступать физическое лицо или компания, что изображается с помощью исключающей ассоциации (рисунок 4.5).
Отношение агрегации
Отношение агрегации имеет место между несколькими классами в том случае, если один из классов представляет собой не которую сущность, включающую в себя в качестве составных частей другие сущности.
Данное отношение применяется для представления системных взаимосвязей типа«часть—целое». Раскрывая внутреннюю структуру системы, отношение агрегации показывает, из каких компонентов состоит система и как они связаны между собой. Это отношение по своей сути описывает декомпозицию или раз биение сложной системы на более простые составные части, которые также могут быть подвергнуты декомпозиции, если в этом возникнет необходимость в последующем. При этом части системы никак не обязаны наследовать ее свойства и поведение, поскольку являются вполне самостоятельными сущностями. Более того, части целого обладают своими собственными атрибута ми и операциями, которые могут существенно отличаться от атрибутов и операций целого.
Агрегация является частным случаем ассоциации и изображается в виде пустой ассоциации с незакрашенным ромбом со стороны «целого» (рисунок 4.6).
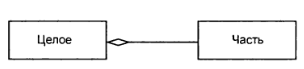
Рисунок 4.6 – Графическое изображение отношения агрегации в языке UML
Примером отношения агрегации может служить деление персонального компьютера на составные части: системный блок, монитор, клавиатуру и мышь (рисунок 4.7).
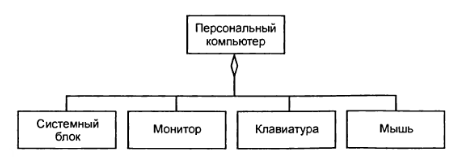
Рисунок 4.7 – Диаграмма классов для иллюстрации отношения агрегации на примере структуры персонального компьютера
Отношение композиции
Отношение композиции является частным случаем отношения агрегации. Это отношение служит для описания специальной формы отношения «часть–целое», при которой составляющие части в некотором смысле находятся внутри целого. Причем части не могут выступать в отрыве от целого, т. е. с уничтожением целого уничтожаются и все его составные части.
Графически отношение композиции изображается сплошной линией, один из концов которой представляет собой закрашенный внутри ромб. Этот ромб указывает на тот из классов, который представляет собой класс-композицию или «целое» (рисунок 4.8).
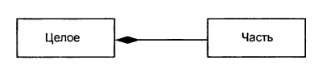
Рисунок 4.8 – Графическое представление отношения композиции в языке UML
Пример отношения композиции – окно интерфейса про граммы, которое может состоять из строки заголовка, кнопок управления размером, полос прокрутки, главного меню, рабочей области и строки состояния. В данном случае наглядно представлено отношение композиции.
В качестве дополнительных обозначений для отношений композиции и агрегации могут использоваться дополнительные обозначения, применяемые для отношения ассоциации. А имен но, указание кратности класса ассоциации и имени данной ассоциации, которые не являются обязательными. Диаграмма классов для класса «Окно_программы», описанного выше, может иметь следующий вид (рисунок 4.9).
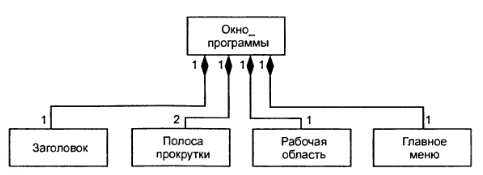
Рисунок 4.9 – Диаграмма классов для иллюстрации отношения композиции на примере класса окна программы
Отношение обобщения
Отношение обобщения является отношением между более общим элементом (родителем или предком) и более частным или специальным элементом (дочерним или потомком). Применительно к диаграмме классов данное отношение описывает иерархическое строение классов и наследование их свойств и поведения. При этом предполагается, что класс-потомок обладает все ми свойствами и поведением класса-предка, а также имеет свои собственные свойства и повеление, которые отсутствуют у класса-предка. Графически отношение обобщения изображается б виде линии с большой незакрашенной стрелкой, направленной на родителя (рисунок 4.10).

Рисунок 4.10 – Графическое изображение отношения обобщения в языке UML
Пример отношения обобщения показан на рисунке 4.10. Здесь абстрактный класс «Геометрическая фигура» выступает в качестве суперкласса (класса-предка) для подклассов (классов-потомков), соответствующих конкретным геометрическим фигурам «Прямо угольник», «Окружность», «Эллипс» и др.
С целью упрощения обозначений на диаграмме классов совокупность линий, обозначающих одно и то же отношение обобщения, может быть объединена в одну линию. В этом случае данные отдельные линии изображаются сходящимися к единственной стрелке, имеющей с ними общую точку пересечения (рисунок 4.11).
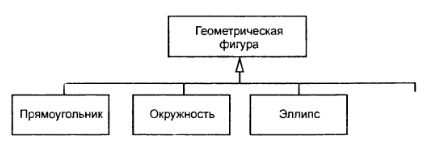
Рисунок 4.11 – Пример графического изображения обобщения классов
Многоточие вместо прямоугольника на диаграмме означает возможность наличия других классов-потомков, не включенных в обозначения представленных на диаграмме классов.
Для того чтобы проиллюстрировать описанные выше типы отношений, рассмотрим следующие пример:
Разработать диаграмму классов для некоей компании — класс «Компаниям», которая состоит из нескольких отделов — класс «Отдел», каждый из которых располагается в своем офисе — класс «Офис», имеет штаб-квартиру класс «Штаб-квартира» и содержит штат сотрудников — класс «Person», сведения о которых содержатся в системе кадрового учета. Каждый из вышеприведенных классов обладает своими атрибутами и операциями и связан с другими классами определенным типом отношений.
Полученная диаграмма приведена на рисунке 4.12.
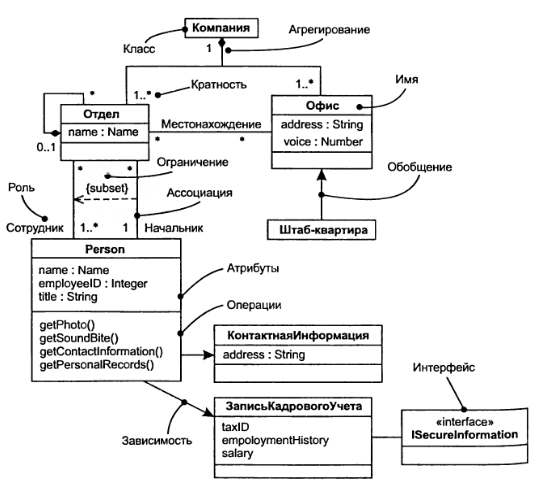
Рисунок 4.12 – Диаграммы классов
Кроме классов на диаграмме могут изображаться интерфейсы.
Интерфейсы
Интерфейс (interface) — именованное множество операций, характеризующих поведение отдельного элемента модели извне без указания их внутренней структуры.
В языке UML интерфейс является специальным случаем класса, у которого имеются операции, но отсутствуют атрибуты. Для обозначений интерфейса на диаграмме классов используется специальный графический символ — окружность, рядом с которой указывается имя интерфейса, или стандартный способ — прямоугольник класса с обозначением «Interface» (рисунок 4.13).