Физика математикалық бағытындағы Назарбаев Зияткерлік мектебі математика пәнінен мектепшілік олимпиада1 тур 11 сынып бойынша математика пәнінен мектепшілік олимпиада тапсырмалары

1. 
   307 ге өсіргенде және 192 ге кеміткенде квадратқа айналатын бүтін санды табыңдар.
   
2. 
   Теңдеуді шешіңдер: (6 - )^x + (6 + )^x=142
   
3. 
   Қабырғасы 1- ге тең дұрыс үшбұрыштың ішінде 5 нүкте орналасқан. Ара қашықтығы 0,5 –тен кем болатың екі нүктенің табылатынындығын дәлелдеңдер.
   
4. 
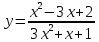   функциясының ең үкен және ең кіші мәндер табыңдар.
   
5. 
   Бірлік квадраттың ішіне 51 нүкте тастады. Радиусы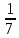 ге тең болатын дөңгелектің ішінде қандай да үш нүкте міндетті түрде болатынын дәлелдеңдер.
   

Назарбаев Интеллектуальная школа физико-математического направления г. АстанаЗадания 1 тура школьной олимпиады по математике в 11 классе

1. 
   Найти целое число, которое обращается в квадрат как при увеличении его на 307, так и после уменьшения на 192.
   
2. 
   Решить уравнение: (6 - )^x + (6 + )^x=142
   
3. 
   Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5
   
4. 
   Найти наименьшее и наибольшее значение функции: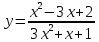
   
5. 
   В единичный квадрат бросили 51 точку. Доказать, что некоторое три из них обязательно лежат внутри круга радиуса .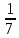
   

Физика математикалық бағытындағы Назарбаев Зияткерлік мектебіматематика пәнінен мектепшілік олимпиада

---

2 тур 11 сынып бойынша математика пәнінен мектепшілік олимпиада тапсырмалары

1. 
   Теңдеулер жүйсін шешіндер: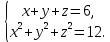
   
2. 
   Геометриялық кескінді қолданып есептеңдер: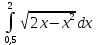
   
3. 
   Өрнекті ықшамдаңдар: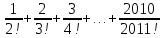
   
4. 
   К нүктесі ABCD тік төртбұрыштың AD қабырғасының ортасы. BK мен AC диагоналының арасындағы бұрышты табыңдар, егер AD:AB=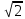 болса.
   
5. 
   Кубқа іштей сфера сызылған. Сфераның әр нүктесінің кубың барлық төбелеріне дейінгі қашықтыңдардын квадраттарынын қосындысы осы нүктеден тәуелсіз екендігін дәлелдеп осы қосындыны табыңдар.
   

Назарбаев Интеллектуальная школа физико-математического направления г. АстанаЗадания 2 тура школьной олимпиады по математике в 11 классе

1. 
   Решить систему уравнений: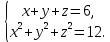
   
2. 
   Пользуясь геометрической интерпретацией определенного интеграла, вычислите: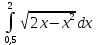
   
3. 
   Упростить выражение: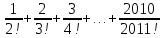
   
4. 
   Точка К – середина стороны AD прямоугольника ABCD. Найти угол между BK и диагональю AC, если известно, что AD:AB=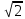
   
5. 
   В куб вписана сфера. Доказать, что сумма квадратов расстояний каждой точки сферы до вершин куба не зависят от выбора этой точки. Найти эту сумму.
   

---

Смотрите также файлы

• Блімі 1блім.docx

• C63c1c83cf8d11ed96ca22f3ddaaab6dдата приема"31" марта 2023 года.pdf

• Номер телефона.docx

• Зияткерлі апаратты орау тсілдері Азаматтыыты атынастарды кпшілігі зияткерлік.docx

• Кодексу Республики Казахстан О здоровье народа и системе здравоохранения.docx