ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТАФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования«Петербургский государственный университет путей сообщения Императора Александра I»(ФГБОУ ВО ПГУПС)Ярославский филиал ПГУПСКонтрольная работа № 1Дисциплина: Метрология, стандартизация и сертификацияСпециальность: 23.05.04 Эксплуатация железных дорогСпециализация: Транспортный бизнес и логистикаФорма обучения – ЗАОЧНАЯВариант: 27Выполнил: Шулёв Д.А. Шифр: 07-005-27-УПТяПреподаватель: Коромыслов В.А. г. Ярославль2022 гКонтрольная работа 1 – Обработка результатов прямых измерений с многократными наблюдениями

Вариант	Результаты измерений										Неисключенные систематические погрешности
27	7.16	7.28	7.31	7.19	7.25	7.31	7.28	7.35	7.28	6.41		0.06	0.09
	7.25	7.36	7.39	7.11	7.18	7.28	7.19	6.37	7.23	7.39

Решение:

1. 
   исключение известных систематических погрешностей из результатов измерений не выполняем, т.к. они не заданы.
   
2. 
   определим среднее арифметическое значение по формуле:
   

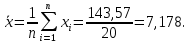
где х_i – i-й результат измерения;n – число исправленных результатов измерений.

3. 
   вычислим среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле (промежуточные расчеты в таблице 1):
   

Таблица 1

№	xi
1	7,16	-0,018	0,000342
2	7,28	0,102	0,010302
3	7,31	0,132	0,017292
4	7,19	0,012	0,000132
5	7,25	0,072	0,005112
6	7,31	0,132	0,017292
7	7,28	0,102	0,010302
8	7,35	0,172	0,029412
9	7,28	0,102	0,010302
10	6,41	-0,768	0,590592
11	7,25	0,072	0,005112
12	7,36	0,182	0,032942
13	7,39	0,212	0,044732
14	7,11	-0,068	0,004692
15	7,18	0,002	0,000002
16	7,28	0,102	0,010302
17	7,19	0,012	0,000132
18	6,37	-0,808	0,653672
19	7,23	0,052	0,002652
20	7,39	0,212	0,044732

---

4. 
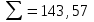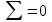   исключим грубые ошибки (промахи), используя критерий Граббса, сравнивая G₁ и G₂ с теоретическим значением G_T при выбранном уровне значимости q.
   

G₁ и G₂ определить по формулам: , 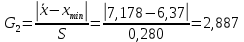.При уровне значимости q=0,05 G_T = 2,709. При выбранном уровне значимости расчетное значение для 6,37 больше теоретического, следовательно оно является промахом и должно быть исключено.

5. 
   определим среднее арифметическое значение :
   

6. 
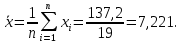
   вычислим среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле (промежуточные расчеты в таблице 2):
   

Таблица 2

№	xi
1	7,16	-0,061	0,0037274
2	7,28	0,059	0,0034748
3	7,31	0,089	0,0079116
4	7,19	-0,031	0,0009643
5	7,25	0,029	0,0008380
6	7,31	0,089	0,0079116
7	7,28	0,059	0,0034748
8	7,35	0,129	0,0166274
9	7,28	0,059	0,0034748
10	6,41	-0,811	0,6578064
11	7,25	0,029	0,0008380
12	7,36	0,139	0,0193064
13	7,39	0,169	0,0285432
14	7,11	-0,111	0,0123327
15	7,18	-0,041	0,0016853
16	7,28	0,059	0,0034748
17	7,19	-0,031	0,0009643
18	7,23	0,009	0,0000801
19	7,39	0,169	0,0285432

---

7. 
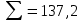   исключим грубые ошибки (промахи), используя критерий Граббса:
   

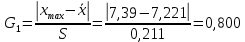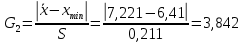, .При уровне значимости q=0,05 G_T = 2,681. При выбранном уровне значимости расчетное значение для 6,41 больше теоретического, следовательно оно является промахом и должно быть исключено.

8. 
   определим среднее арифметическое значение :
   

9. 
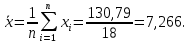
   вычислим среднее квадратическое отклонение S группы, содержащей n результатов измерений по формуле (промежуточные расчеты в таблице 3):
   

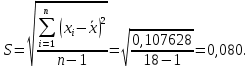
Таблица 3

№	xi
1	7,16	-0,106	0,01126
2	7,28	0,014	0,000193
3	7,31	0,044	0,001926
4	7,19	-0,076	0,005793
5	7,25	-0,016	0,00026
6	7,31	0,044	0,001926
7	7,28	0,014	0,000193
8	7,35	0,084	0,007037
9	7,28	0,014	0,000193
10	7,25	-0,016	0,00026
11	7,36	0,094	0,008815
12	7,39	0,124	0,015348
13	7,11	-0,156	0,024371
14	7,18	-0,086	0,007415
15	7,28	0,014	0,000193
16	7,19	-0,076	0,005793
17	7,23	-0,036	0,001304
18	7,39	0,124	0,015348

---

10. 
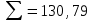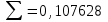    исключим грубые ошибки (промахи), используя критерий Граббса:
    

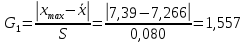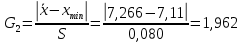, .При уровне значимости q=0,05 G_T = 2,651. При выбранном уровне значимости расчетные значения меньше теоретического, следовательно промахов нет.

11. 
    рассчитаем среднее квадратическое отклонение среднего арифметического (оценки измеряемой величины)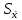 по формуле:
    

12. 
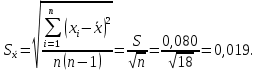
    проверим гипотезу о том, что результаты измерений принадлежат нормальному распределению.
    

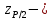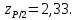
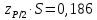
Считают, что результаты измерений принадлежат нормальному распределению, если не более m разностей превысили значение , где S – среднее квадратическое отклонение, верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности P/2.Так как число измерений у нас n=18, то P=0,98 и Закон распределения соответствует нормальному, ни одна разность (из одной возможной) не превышает вычисленное значение.

13. 
    Вычислим доверительные границы случайной погрешности по формуле:
    

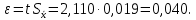
t – коэффициент Стьюдента, при P=0,95 и n-1=17 t=2,110.

14. 
    Вычислим границы неисключенной систематической погрешности (НСП)
    

Границу НСП 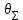оценки измеряемой величины при наличии менее 3-х (m < 3) НСП, каждая из которых представлена границами 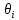оценивают по формуле: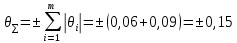

15. 
    Вычислим доверительные границы погрешности результата измерения.
    

Вычислим среднее квадратическое отклонение НСП, которое оценивают по формуле:

---

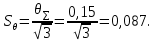
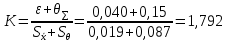
Вычислим суммарное среднее квадратическое отклонение оценки измеряемой величины, вычисляемое по формуле:Коэффициент К вычислим по формуле:Доверительные границы погрешности результата измерения:

16. 
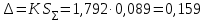
    Запишем результат измерения.
    

Согласно ГОСТ 8.736.2011 погрешность округляется до двух значащих цифр так как первая значащая цифра не более трех (равна 1). Последнюю сохраняемую цифру увеличиваем на 1 так как отбрасываемая больше 5 (равна 9). В итоге .Результат округляем до того же знака, что и погрешность.При симметричных доверительных границах погрешности результат измерения представляют в форме:

---

Смотрите также файлы

• Лекция тема 8 бюджетноналоговая (фискальная) и денежнокредитная (монетарная) и политики государства.docx

• Методические подходы к анализу кредитоспособности корпоративных заемщиков.docx

• Решение задачи Пятиклассник переходный от младшего возраста к подростковому возраст. Возраст связан с постепенным обретением чувства взрослости. Характерно усиление независимости детей от взрослых. Характерен негативизмстремление противостоять.docx

• Как не навредить себе при работе закомпьютером.docx

• Характеристика коллектива 10 класса.docx