Вариант № 9Задачи под номерами: 1.24; 1.34; 2.29; 2.59; 3.151.24. С покоящимся шаром массой т = 4 кг сталкивается такой же шар, движущийся со скоростью υ = 1 м/с. Вычислить работу, совершенную вследствие деформации при прямом центральном неупругом ударе.Дано: m₁=m₂= m = 4кг υ₁ – 1м/сυ₂ – 0Найти: АРешение:таккакударшаровнеупругий,топослеударашарыбудут двигаться с общей скоростью V. 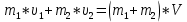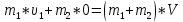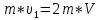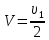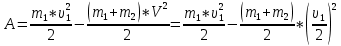Закон сохранения импульса при этом удареимеетвид:После упрощения получаем выражение:Следовательно, Работа в следствии деформации равна разнице энергий до и после удара.Ответ: A=1 Дж.1.34. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению, где А =2 рад/с; В =0,2 рад/с 3. 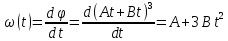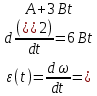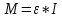Определить 3 ϕ += BtAt вращающий момент М, действующий на стержень в момент времени t = 2 с, если момент инерции стержня I = 0,048 кг⋅м².Дано: I=0.048 кг*м³φ=At+Bt³ A=2 рад/c B=0.2 рад/c³ T=2 cНайти: MРешение: найдем как изменится угловое ускорение стержня:Основное уравнение вращательного движения твердого тела относительно неподвижной оси:где ε – угловое ускорение

---

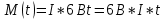
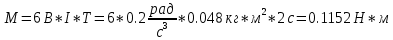
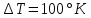
I – момент инерции телаТо есть вращающий момент будет расти со временем по закону:Найдем вращающий момент , действующий на стержень через время T после начала вращения:Ответ: M=0.1152 Н*м 2.29. Определить, какое количество теплоты необходимо сообщить аргону массой т = 400 г, чтобы нагреть его на ΔТ = 100 К: а) при постоянном объеме; б) при постоянном давлении.Дано:m(Ar)=400гр=0,4 кг M=0.04 кг/моль.Найти: Q_v, Q_pРешение: Количество теплоты, сообщаемое аргону, определяется по формулам: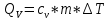(1)(2)где с_v, с_р – удельные теплоёмкости аргона при постоянном объёме и при постоянном давлении, m – его масса, Т – температура, на которую был нагрет аргон.Удельные теплоёмкости с_V, с_р связаны с молярными теплоёмкостями С_V, С_р соотношениями: 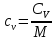(3) (4)где М – молярная масса аргона.Молярные теплоёмкости определяются по формулам: (5) (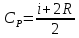6)где i= 3 – число степеней свободы молекулы аргона, R – газовая постоянная.С учётом (3), (4), (5), (6) соотношения (1) и (2) можно записать в виде 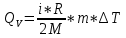(7) (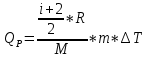8)Подставляя в (7) и (8) числовые значения, находим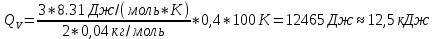Ответ: Q_v= 12,5 кДж,Q_p= 20,8 кДж.2.59. Совершая цикл Карно

---

, газ получил от нагревателя теплоту Q₁ = 500 Дж и совершил работу А = 100 Дж. Температура нагревателя T₁ = 400 К. Определить температуру Т₂ охладителя.

Дано: Q₁ = 500 Дж

А = 100 Дж

T₁ = 400 К.

Найти: Т₂

Решение: Рассчитаем КПД цикла Карно:



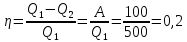
Но для цикла Карно так же справедливо отношение:



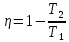
Отсюда для Т₂ получим:



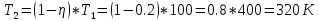
Ответ: Т₂=320 K

3.15. Поверхностная плотность заряда σ бесконечно протяженной плоскости равна 400 мкКл/м². К плоскости на нити подвешен заряженный шарик массой m = 10 гр. Определить заряд Q шарика, если нить образует с плоскостью угол α = 30°.

Дано: m = 10гр = 0,01кг

σ = 400 мкКл/м²

α = 30°.

Найти: Q

Р ешение:

На рисунке укажем действующие силы. Поскольку шарик находится в

равновесии, то равнодействующая сил равна нулю:


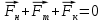
(1)

г де 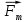– сила тяжести, 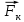– сила кулоновского взаимодействия шарика и плоскости

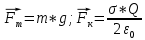(2)

Спроецируем уравнение (1) на оси координат обозначив угол между плоскостью и нитью через α и учтя выражение (2)

Ось OX:

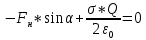
Ось OY:

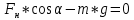
Выразим из этих выражени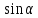й и :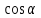





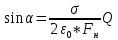
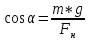
Разделим первое на второе:



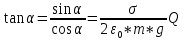
Из последнего выразим и вычислим Q:

---

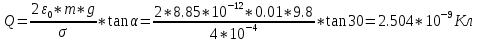
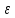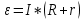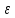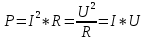
Ответ: 3.56. Внешняя цепь источника тока потребляет мощность Р = 0,75 Вт. Определить силу тока в цепи, если ЭДС источника тока ε = 2 В и внутреннее сопротивление r = 1 Ом.Дано:P = 0.75 Вт = 2 Вr = 1 Ом.Найти: IРешение: напишем закон Ома для полной цепи: , где – ЭДС цепи, R- внешнее сопротивление, r – внутреннее сопротивление, I – сила тока. 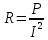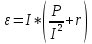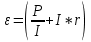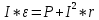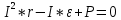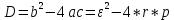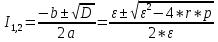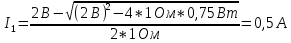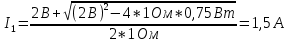Так же напишем формулу для мощности:Воспользуемся этой формулой и выразим R, затем подставим в ранее написанный закон Ома: ; и преобразовав получим: , далее помножим на I чтоб избавиться от знаменателя , далее перенесем в правую частьНайдем дискриминант:Подставим наши значения и получим результат:Ответ: I₁=0.5; I₂=1.5

---

Смотрите также файлы

• Решение так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью V.doc

• Оу бадарламасына сйкес оыту масаты.docx

• Повторение. Иррациональные числа.docx

• Fill in with Present Simple or Continuous.docx

• Титульный лист Специфика маркетинга на примере транспортного предприятия.docx