Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

.

Второй закон Кирхгофа: алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжения на всех участках контура:

.

В общем случае токи сложной электрической цепи могут быть определены в результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа. Количество уравнений (m) должно быть равно количеству неизвестных токов цепи. Порядок расчета:

1) произвольно намечают направления токов ветвей, и если цепь имеет n узлов, то по первому закону Кирхгофа записывают (n – 1) уравнений, так как уравнение для n-го узла является следствием предыдущих;

2) произвольно намечают направления обхода контуров и по второму закону Кирхгофа записывают m (n – 1) уравнений. При этом контуры выбирают так, чтобы каждый из них содержал хотя бы одну не учтенную ранее ветвь;

3) решая систему m уравнений, находят токи. Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным.

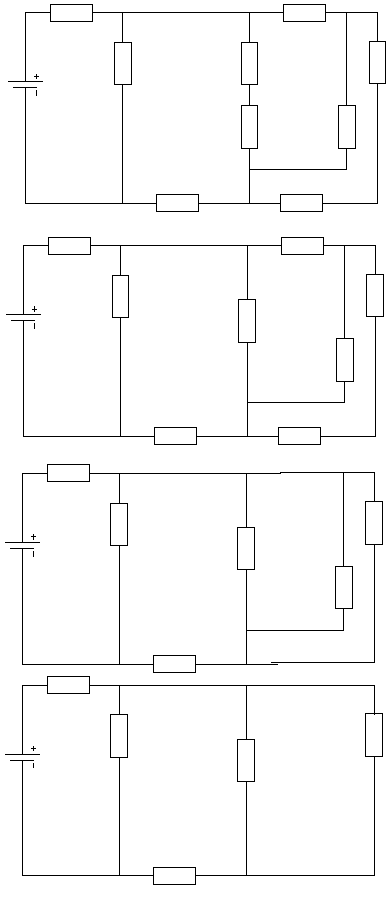
Для электрической цепи рис. 1.1 n = 2, m = 3, и расчет токов цепи осуществляется путем решения следующей системы уравнений:

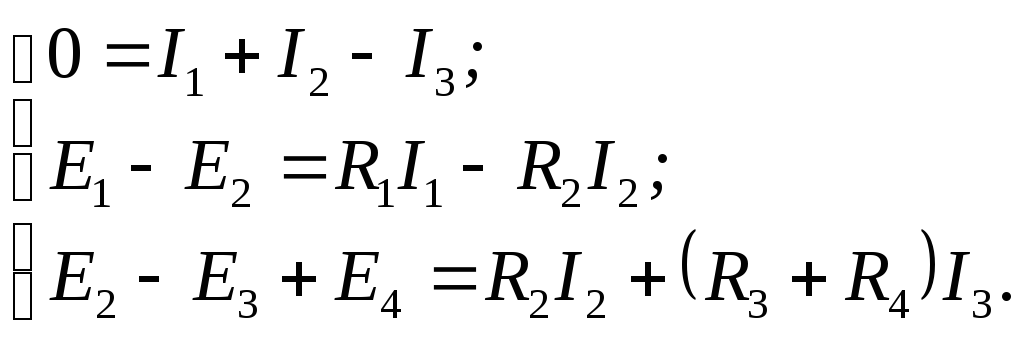
Метод контурных токов позволяет уменьшить общее число уравнений на (n – 1) и свести систему к числу m – (n – 1) уравнений, составленных по второму закону Кирхгофа.

Последовательность расчета:

1) цепь разбивают на отдельные контуры и в каждом контуре произвольно выбирают направление условно действующего контурного тока, замыкающегося только в данном контуре;

2) выбрав обход контуров совпадающим с направлением контурных токов, для каждого контура записывают уравнение по второму закону Кирхгофа, при этом учитывают падения напряжения на элементах рассматриваемого контура и от соседних контурных токов;

3) решая полученную систему уравнений, находят контурные токи;

---

4) действительные токи ветвей определяются алгебраическим суммированием контурных токов, протекающих в них.

Например, для электрической цепи, схема которой приведена на рис. 1.1, получим следующие уравнения:

.

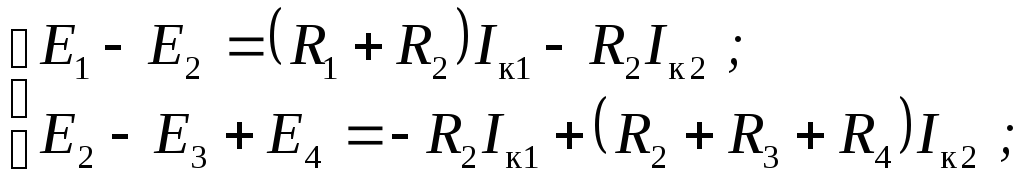
Действительные токи в ветвях

I₁ = I_к1; I₂ = I_к2 – I_к1; I₃ = I_к2.

Метод наложения основан на принципе наложения, согласно которому в линейной электрической цепи, содержащей несколько источников питания, токи ветвей рассматривают как алгебраическую сумму токов, вызываемых в этих ветвях действием каждой ЭДС в отдельности. Последовательность расчета:

1) в цепи поочередно оставляют по одному источнику питания и получают расчетные схемы, число которых равно числу источников питания (внутренние сопротивления исключенных источников оставляют в цепи);

2) определяют токи всех ветвей расчетных схем, используя методы преобразования цепей;

3) действительные токи ветвей находят суммированием (наложением) соответствующих токов расчетных схем с учетом их направлений.

Эффективен этот метод для расчета цепей, содержащих небольшое число источников.

Метод двух узлов применяется для расчета цепей, имеющих только два узла. Сущность метода заключается в определении напряжения между узлами, после чего токи ветвей находят по обобщенному закону Ома. Порядок расчета:

1) произвольно выбирают направление узлового напряжения U_ab и определяют его величину по формуле:

,

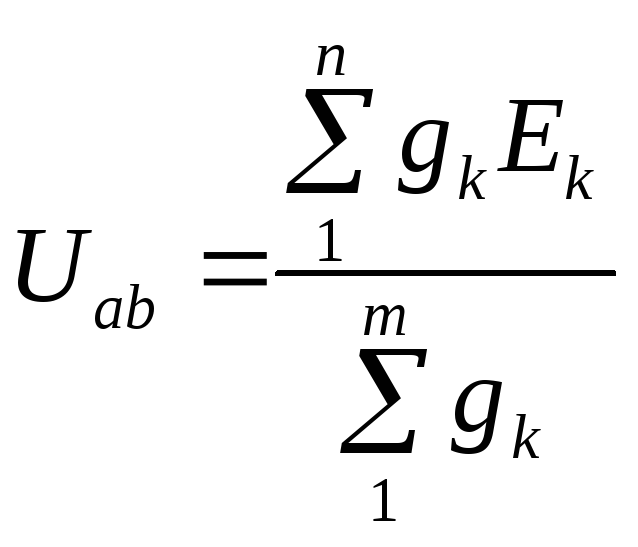где – алгебраическая сумма произведений суммарной ЭДС ветви и суммарной проводимости ветви (ЭДС, входящие в ветвь, берут со знаком плюс, если их направления противоположны направлению напряжения U_ab, и со знаком минус, когда их направления совпадают с направлением U_ab);

– сумма проводимостей всех ветвей цепи.

Например, для цепи рис. 1.1 узловое напряжение

---

;

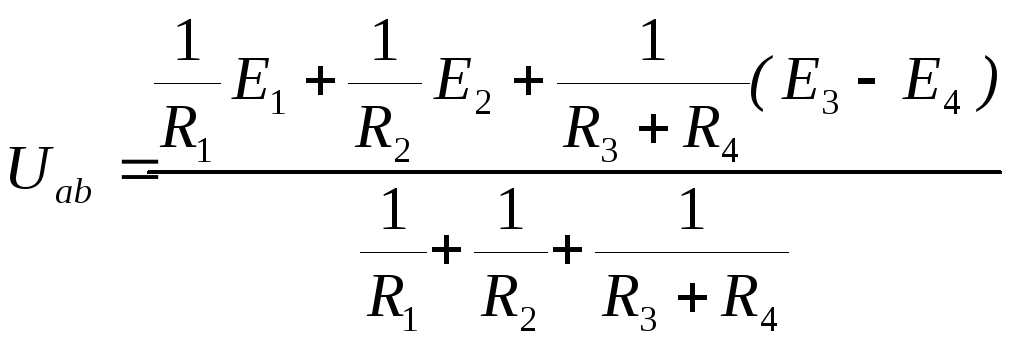2) рассчитывают токи в ветвях по обобщенному закону Ома (для цепи рис. 1.1 – уравнения (1.1)).

Метод эквивалентного генератора применяется в тех случаях, когда требуется определить ток только в одной ветви сложной цепи. При этом выделяют расчетную ветвь (или участок ветви), а всю остальную часть цепи заменяют эквивалентным генератором с ЭДС Е_э и внутренним сопротивлением R_э.

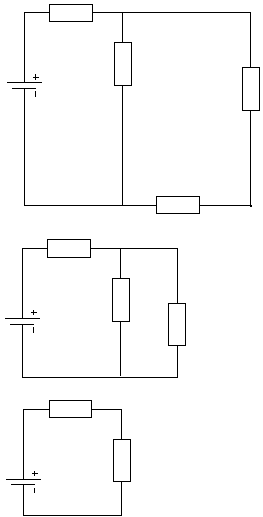
Например, для расчета тока I₃ в цепи (см. рис. 1.1) соответствующая замена показана на рис. 1.2., тогда .

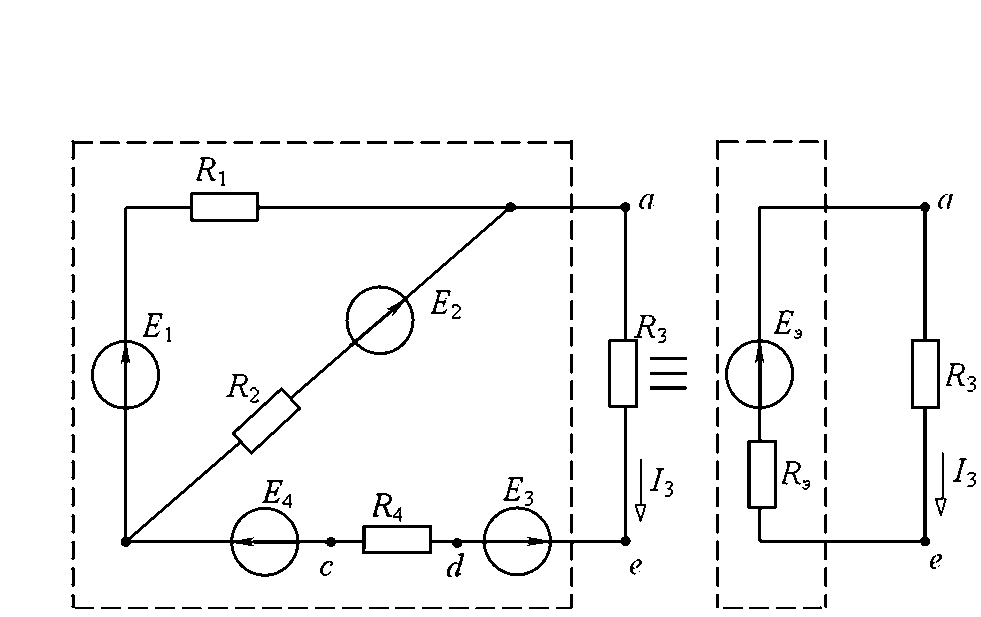
Рис. 1.2

Параметры эквивалентного генератора Е_э, R_э определяются аналитически либо экспериментально. ЭДС Е_э равна напряжению на разомкнутых зажимах расчетной ветви (напряжению холостого хода) U_{ае х} (рис.1.3, а) и может быть рассчитана или измерена вольтметром. Так, аналитически напряжение U_{ае х} в цепи (см. рис. 1.3, а) выражается уравнением U_{ае х} = Е₁ – Е₃ + Е₄ – R₁I_х,

где .

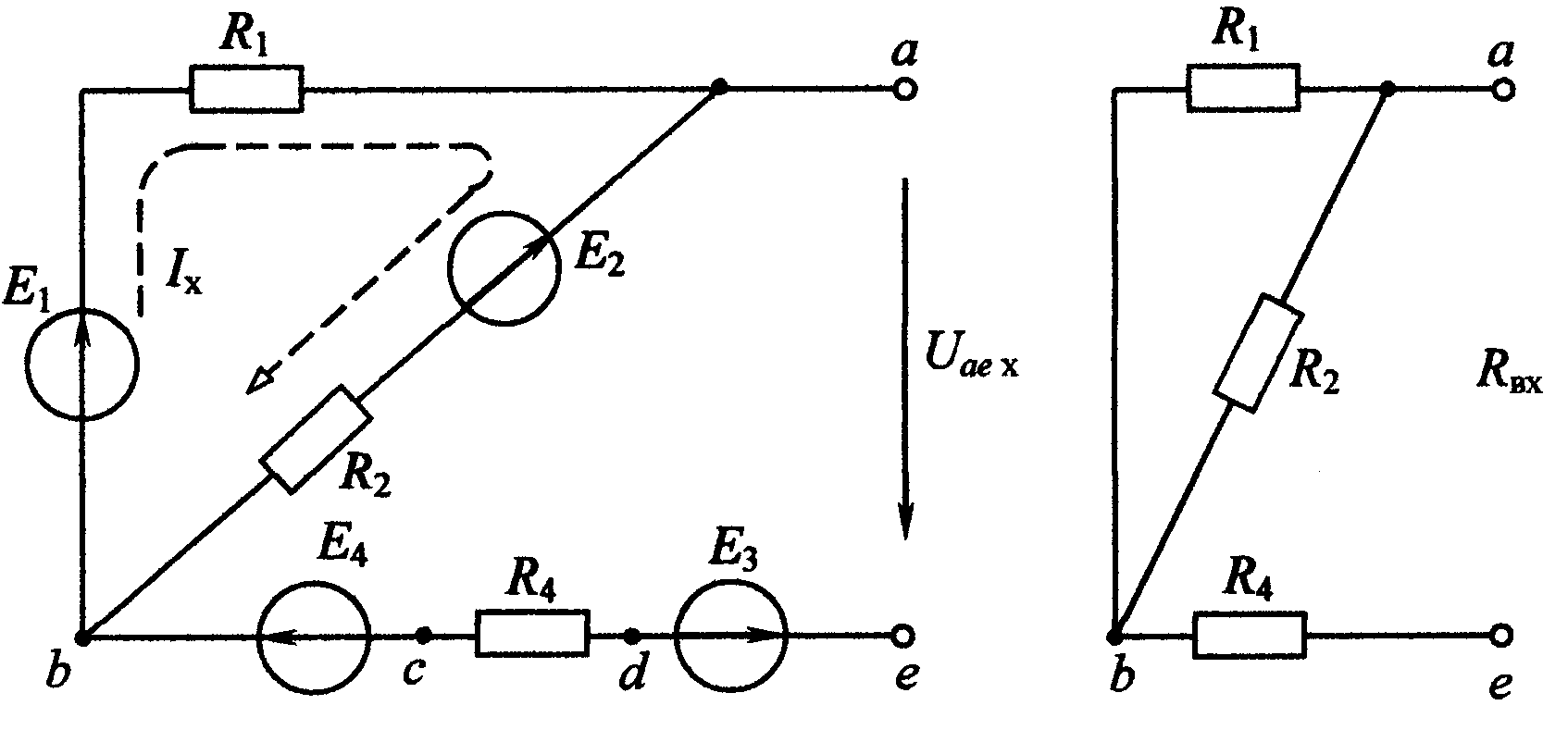
а б

Рис. 1.3

Внутреннее сопротивление R_э равно входному сопротивлению цепи R_вх по отношению к зажимам выделенной ветви (участка). Для расчета R_вх исключают все источники ЭДС и сворачивают пассивную часть цепи относительно зажимов ае (рис. 1.3, б).

.

Оно может быть измерено косвенно, как R_вх = U_{ае х} / I_3к, где I_3к – ток расчетной ветви при коротком замыкании выделенного участка ае.

Тогда искомый ток

---

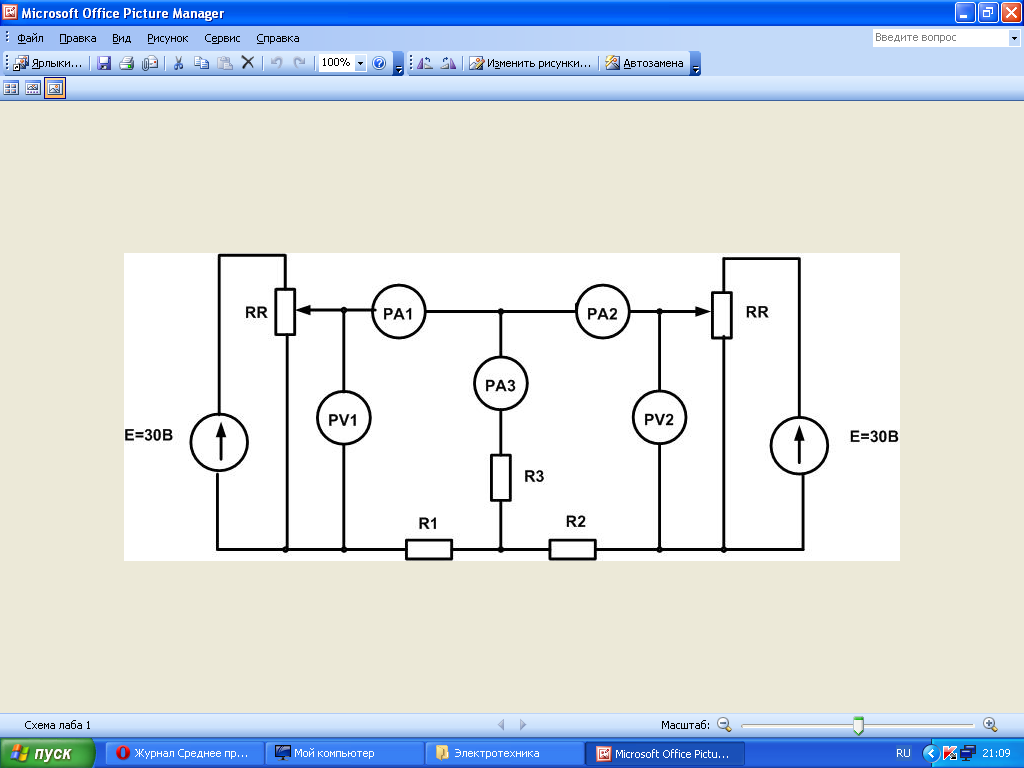
рис. 1.4

Т а б л и ц а 1

№ изм.	Измерения								Вычисления			Метод расчета
	Е1, В	Е2, В	R1,Ом	R2,Ом	R3, Ом	I1, мА	I2, мА	I3, мА	I1, мА	I2, мА	I3, мА
1	12	12	50	100	200	34,7	17,4	52,2	0,0342857	0,0171428	0,0514285	Законы Кирхгофа
									0,0343	0,017 14	0,05144	Метод контурных токов
2	12	22	50	100	200	20,7	88,1	66,6	0,022857	0,0885714	0,065714	Законы Кирхгофа
									0,02285	0,088571	0,06571	Метод контурных токов
3	12	-12	50	100	200	168,4	152,7	16,5	0,1644256	0,1527457	0,0165561	Законы Кирхгофа
									0,16442	0,15274	0,01655	Метод контурных токов

---

Закон Кирхгофа:

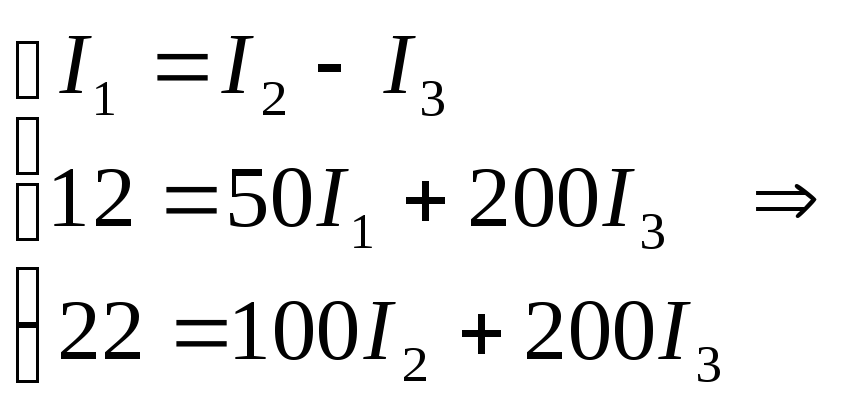
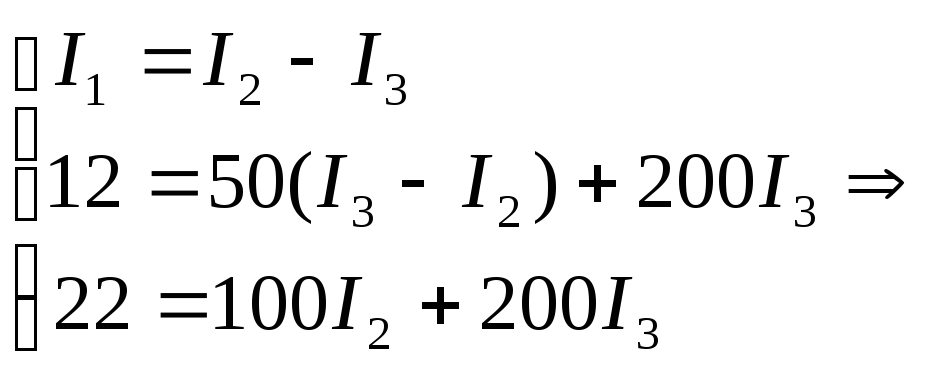
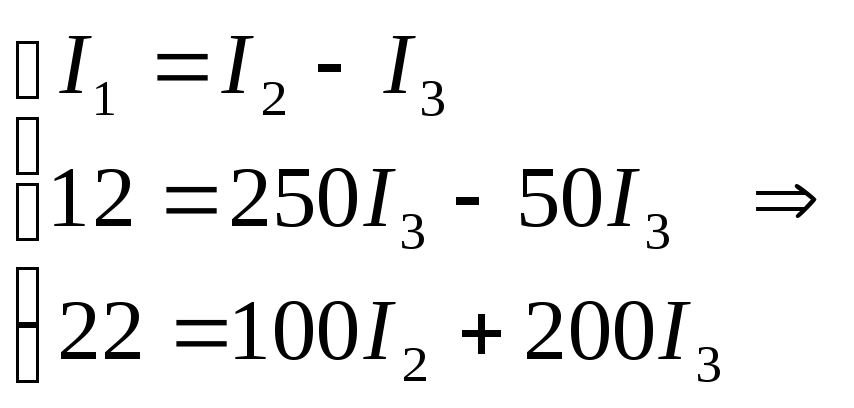
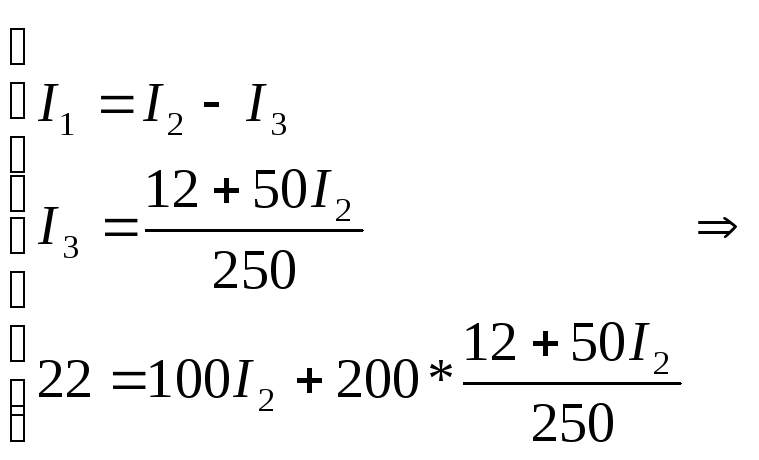
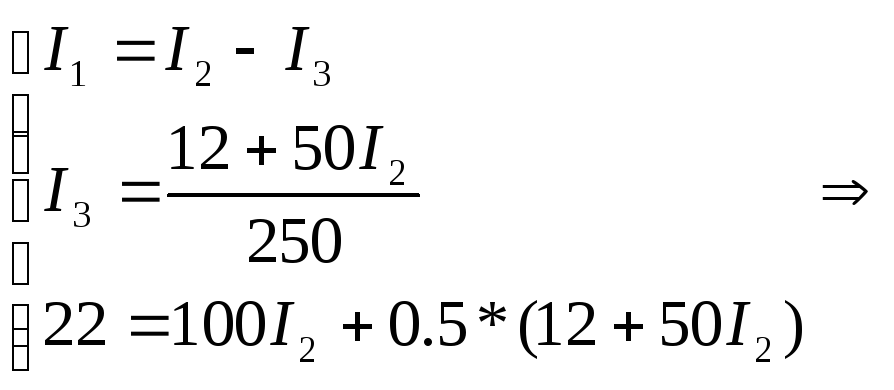
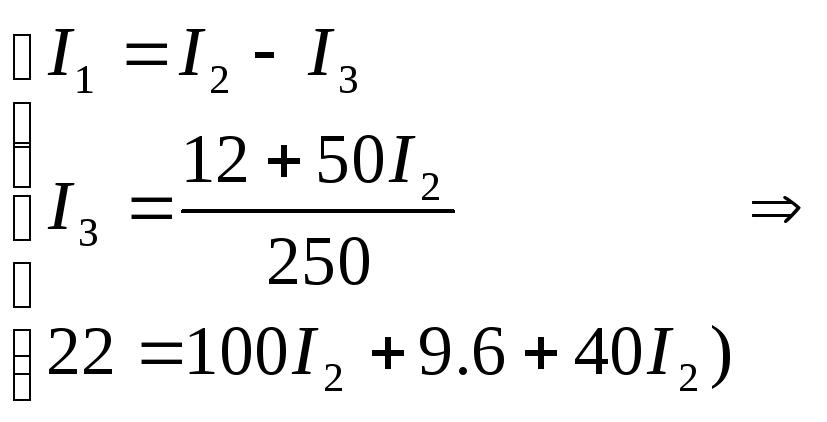
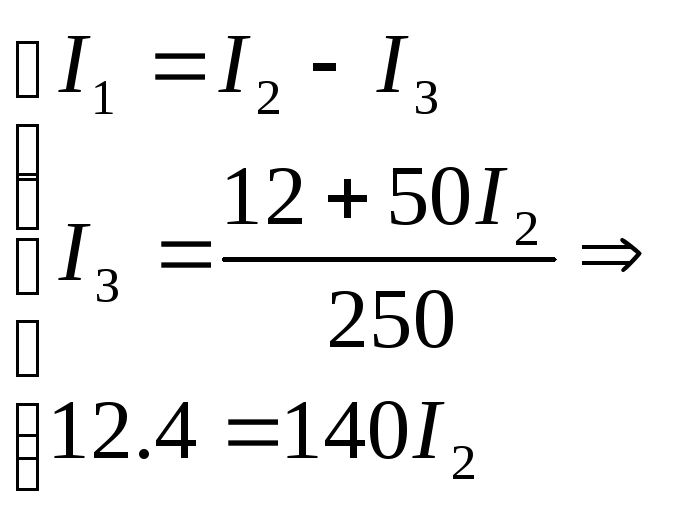
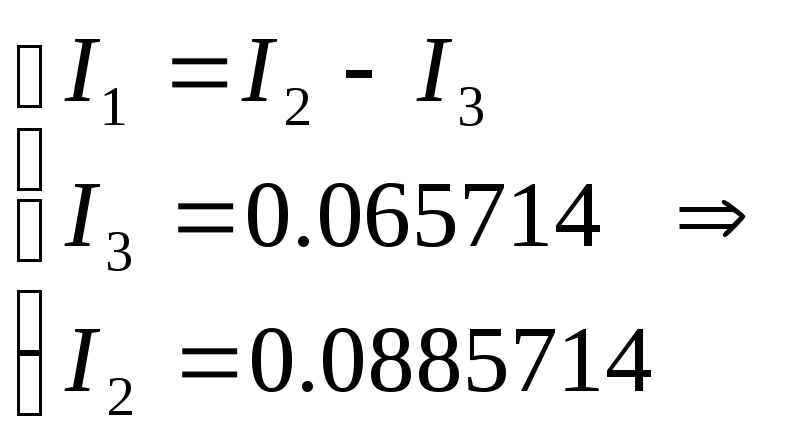
Метод контурных токов:

;

;

;

;

;

---

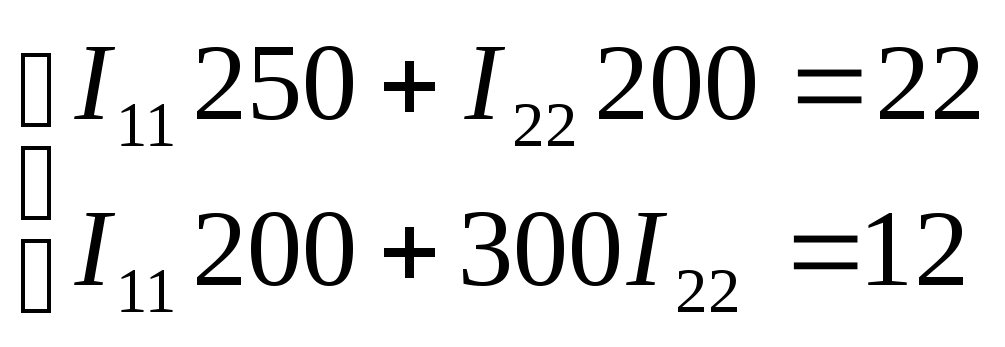
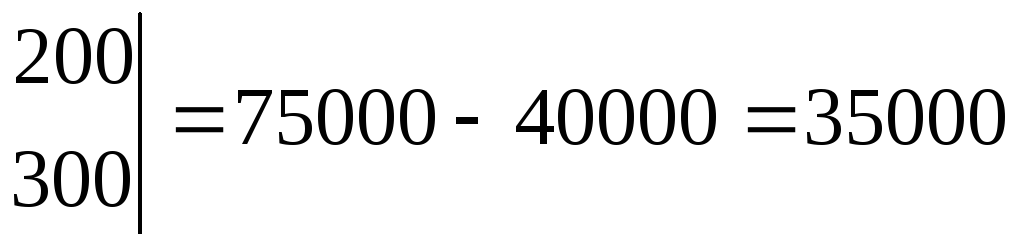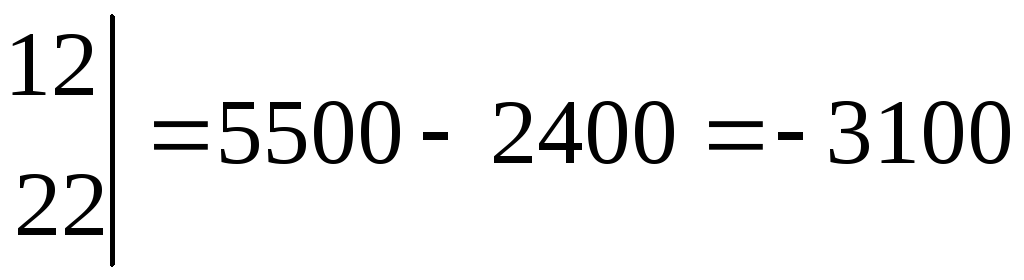Смотрите также файлы

• Лаб_раб_№1.doc

• Лаб_раб_2.doc

• Лекционный курс НП.doc

• Титул лист.doc

• 6.doc