ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 67
Скачиваний: 0
.
Пусть сущ-т подпр-во
размерности
,
на которм
отриц определена. Тогда, т.к.сумма
размерностей
и
больше
,
эти подпр-ва имеют ненулевой вектор
в пересечении. Имеем
т.к.
и
,
т.к.
.
Получ противоречие, показывает, что
.
Число коэф-ов, равных -1, равно отрицат
индексу и поэтому не зависит от базиса.
Число коэф-ов , = +1, также не зависит от
базиса, т.к.оно равно
а ранг
и индекс
от базиса не зависят. Ч.т.д.
Следствие: число положит и число отрицат коэф-ов в любом диагонал виде квадр формы не зависят от базиса.
Б2 1.1 Решим систему методом Гаусса
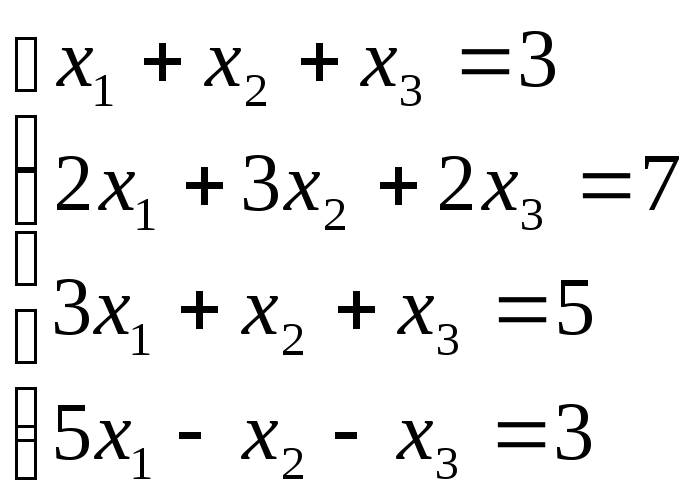
Решение.
=
=
=
=
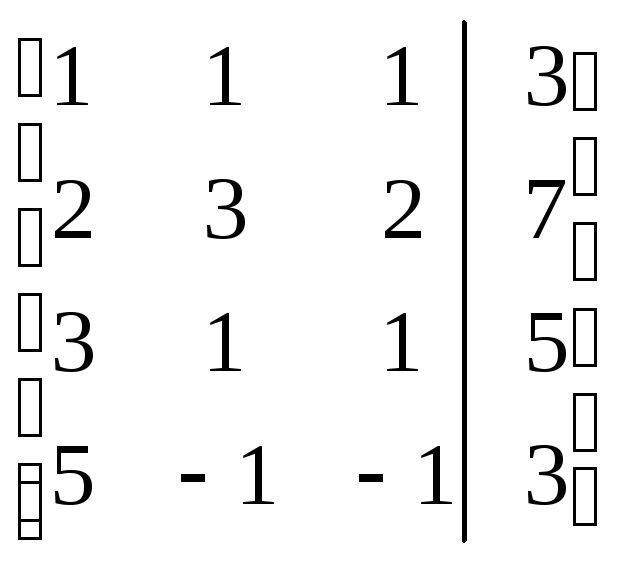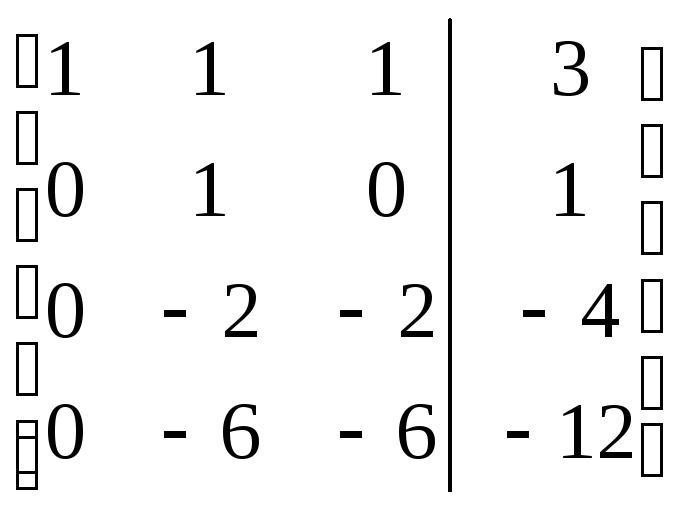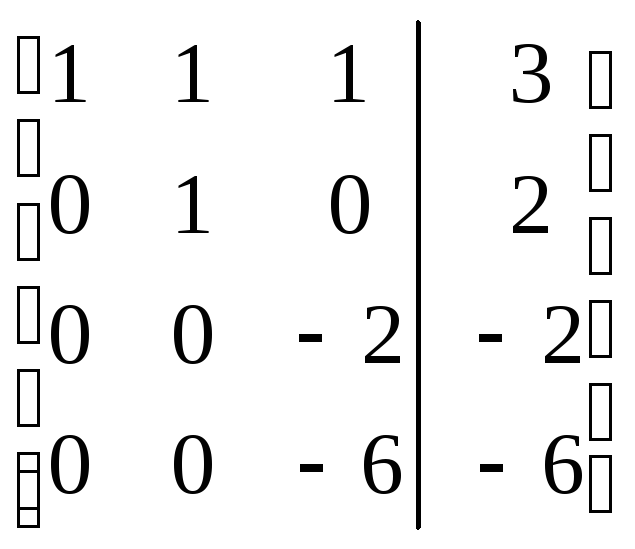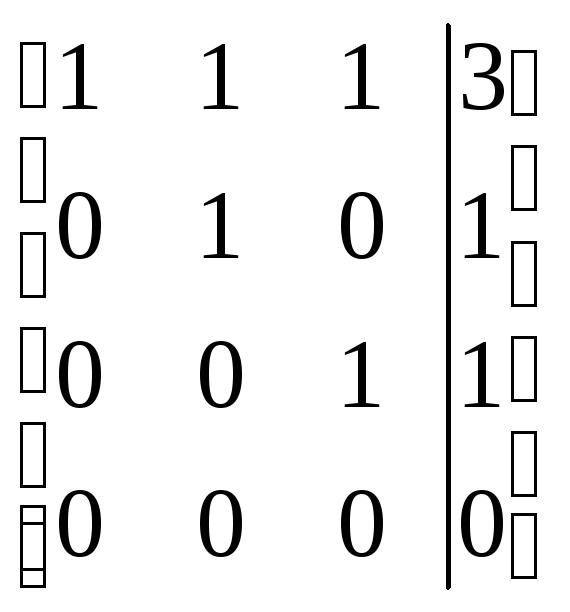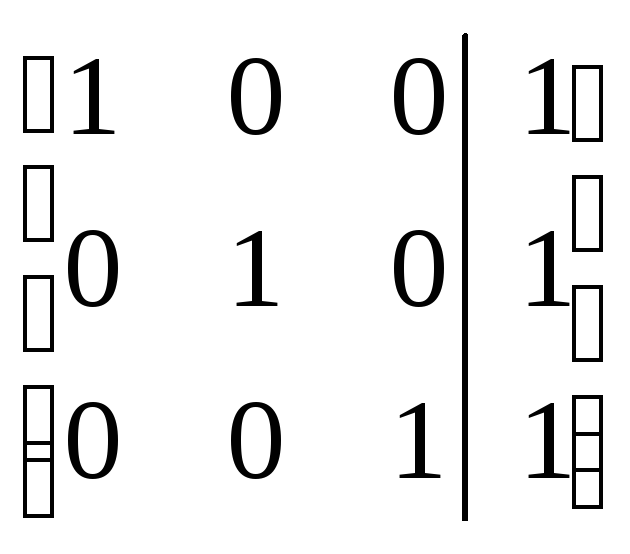
Имеем ранг матрицы
-число
ненулевых строк
2 ур-ия исходной системы линейно независ.
Ответ:
,
Б2 1.2 Решить систему, пользуясь формулами Крамера.
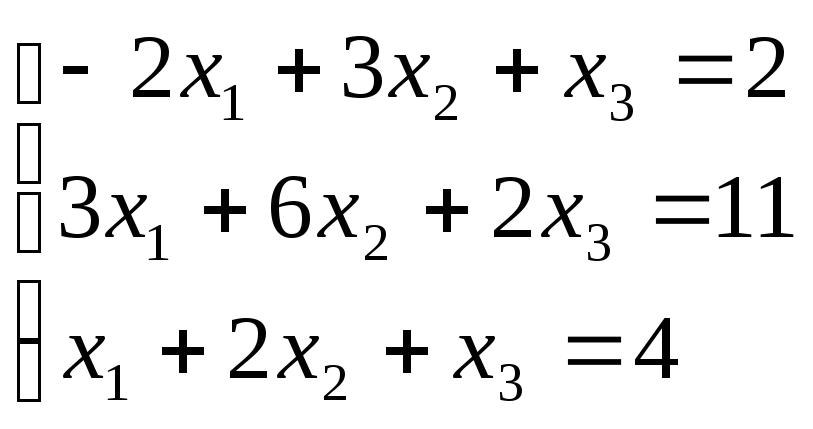
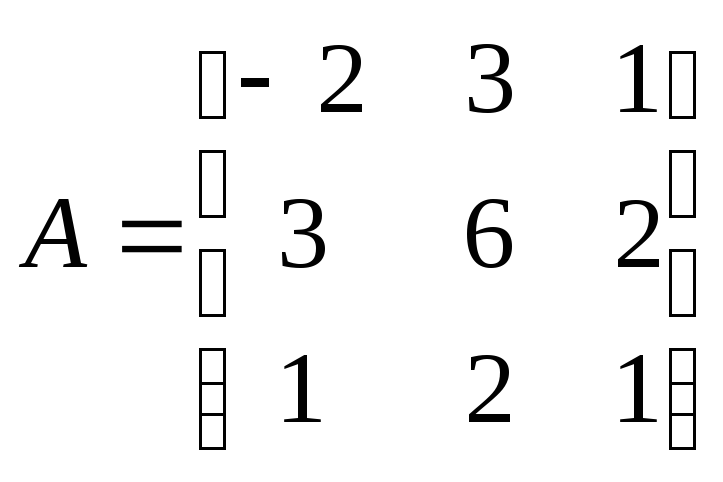
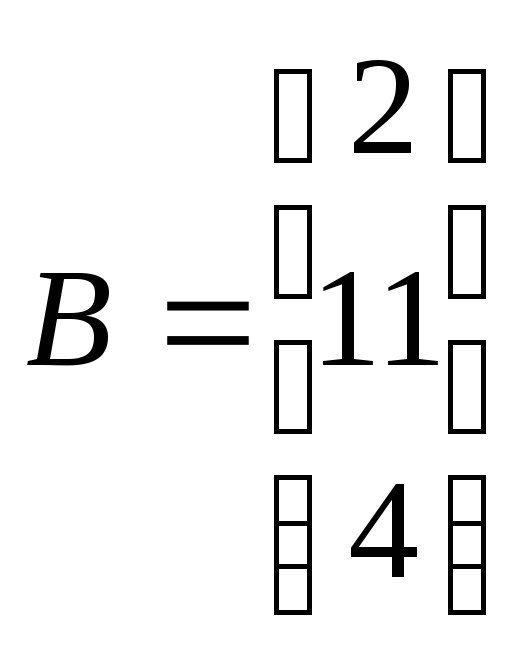
Итак,
,
,
,
,
.
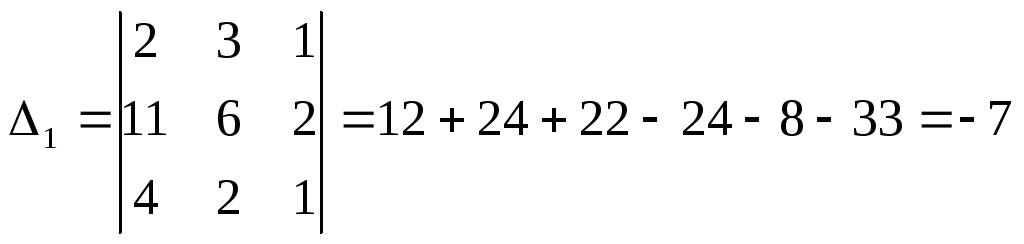
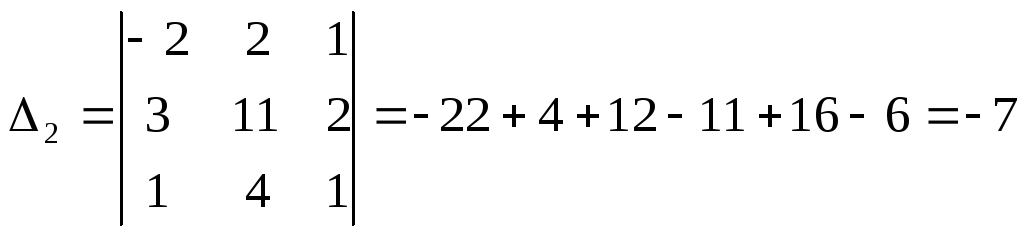
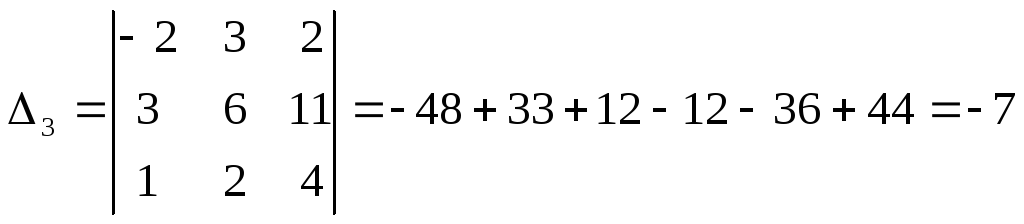
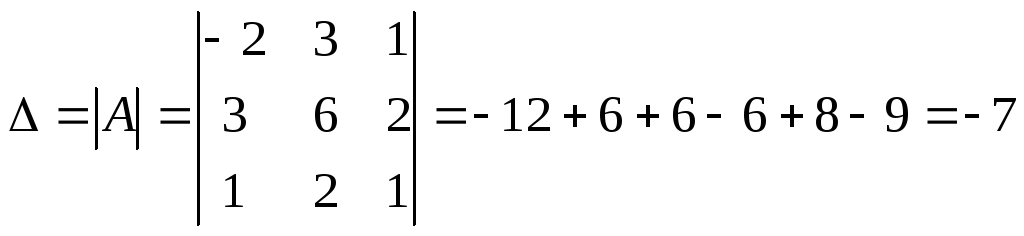
Ответ:
Б2 1.3 Решить систему лин однор ур-ий
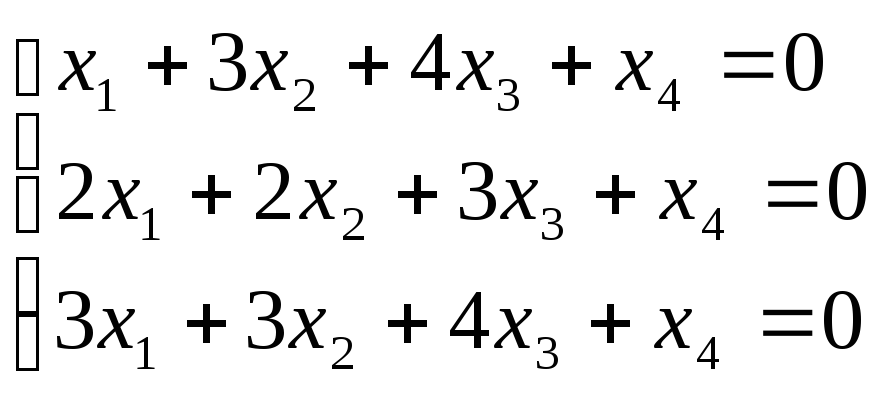
Решаем с помощью метода Гаусса
=
=
=
=
=
=
-
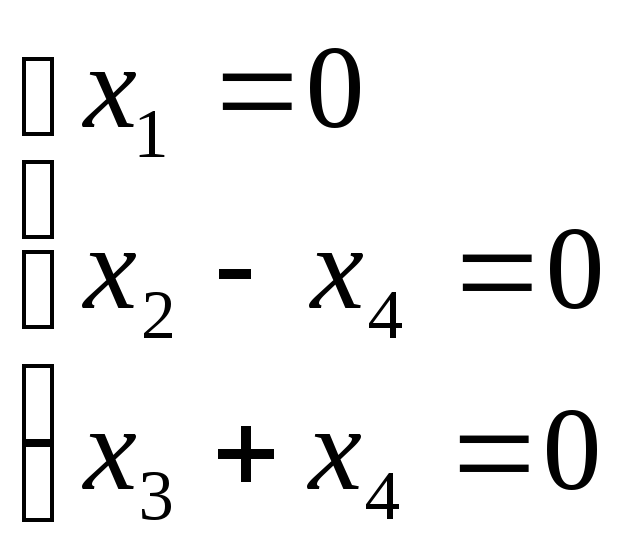
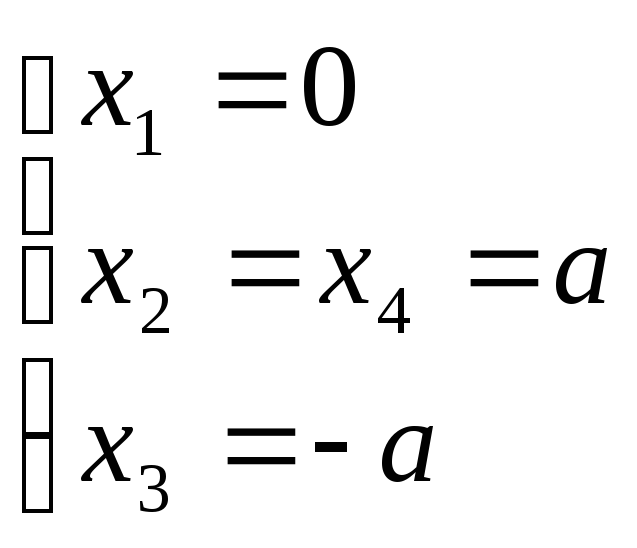
любое действительное число
Ответ :
Б2 2.1 Лин
преобразование
лин пр-ва
имеет в базисе
,
,
матрицу
.
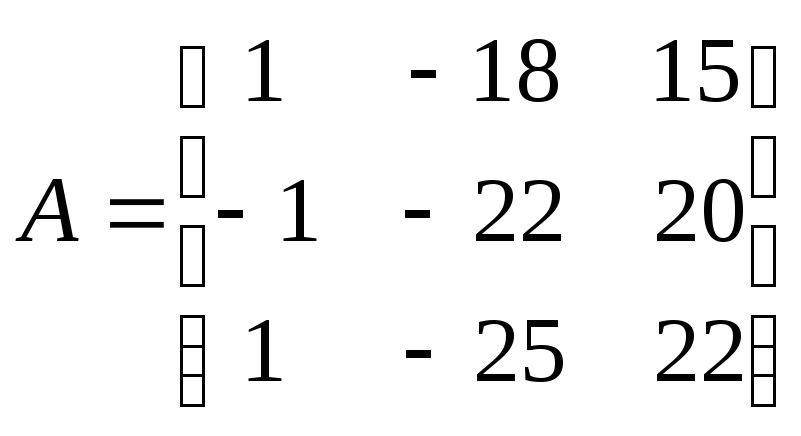Найти матрицу
того же преобраз в базисе
,
,
,
-матрица
перехода от1 базиса ко 2-ому
,
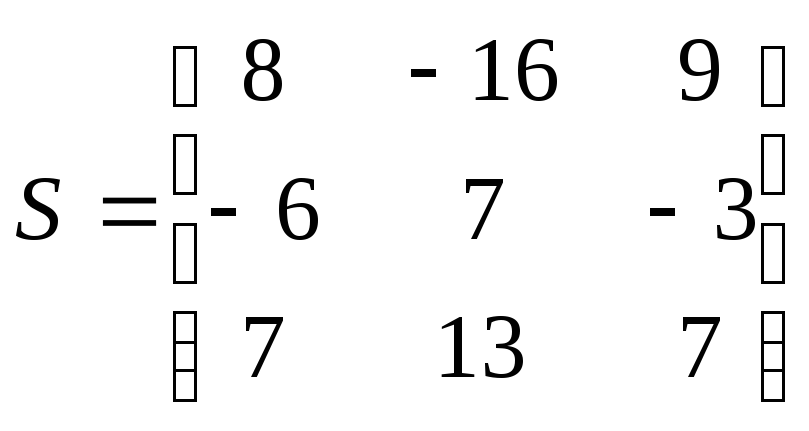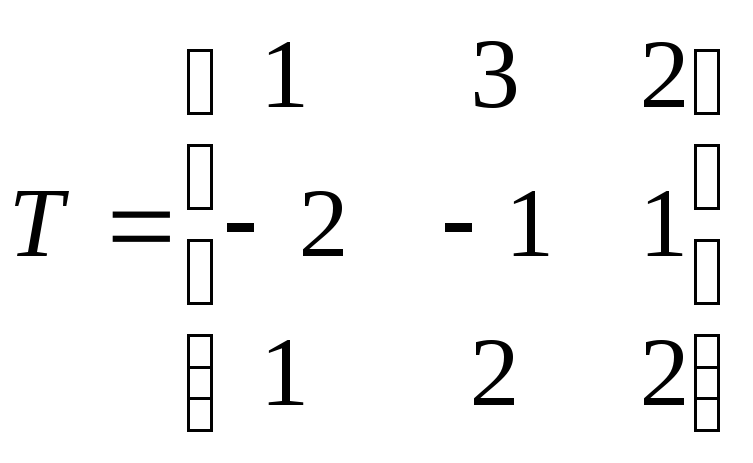
Т.к.
,
-
базисы, то их матрицы
-невырожденные,
,
поэтому
,
т.е.
-матрица
перехода от базиса
к базису
.
Отсюда
и решим ур-ие
.
.
Б2 2.2 найти ядро
и дефект линейного преобразования
пространства
,
если
в некот базисе задано матрицей
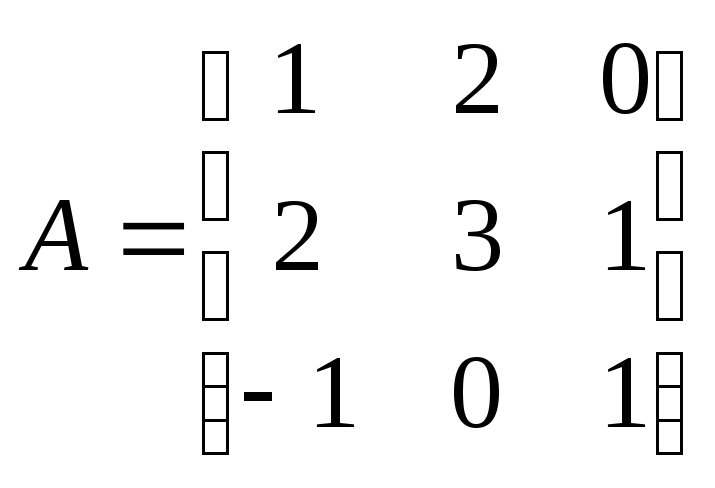
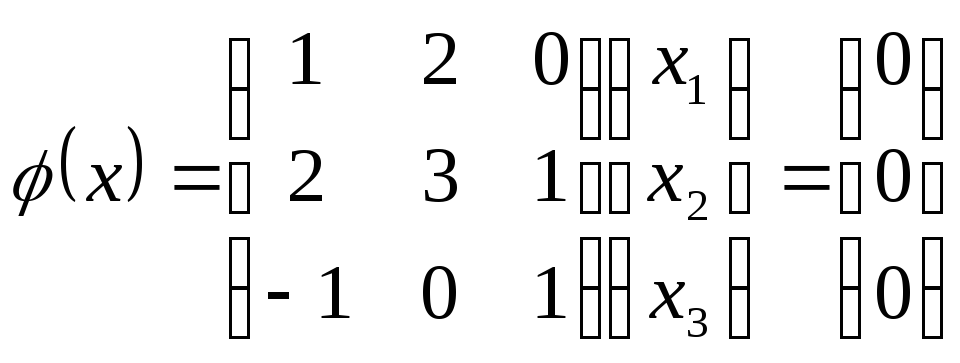
Т.е.
соответствует пр-ву решений системы:
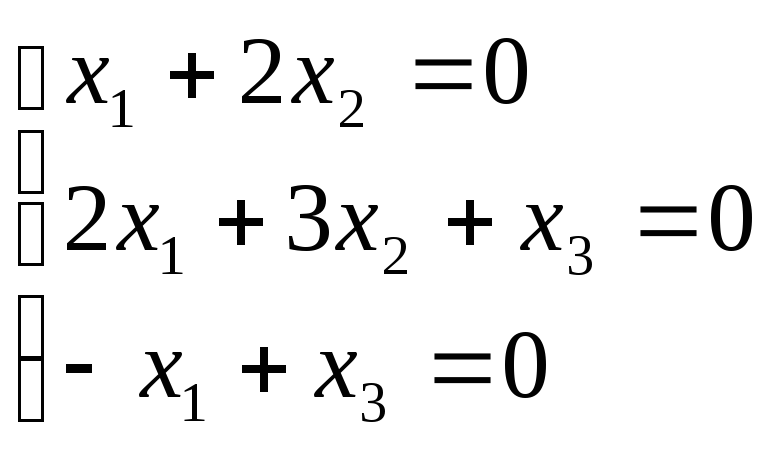
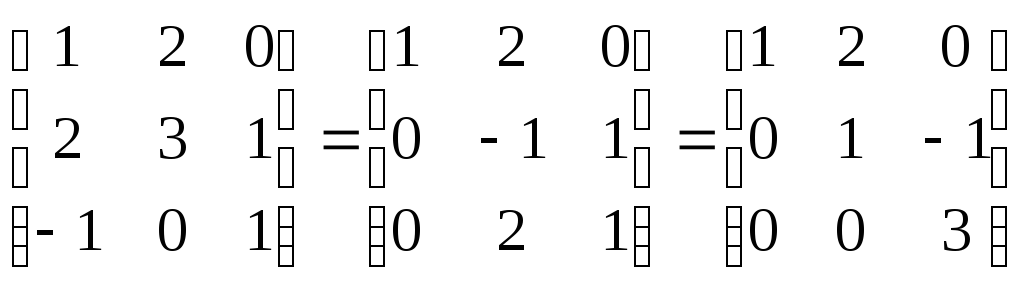-треугол.вида
,
,
система имеет
единств решение
,
,
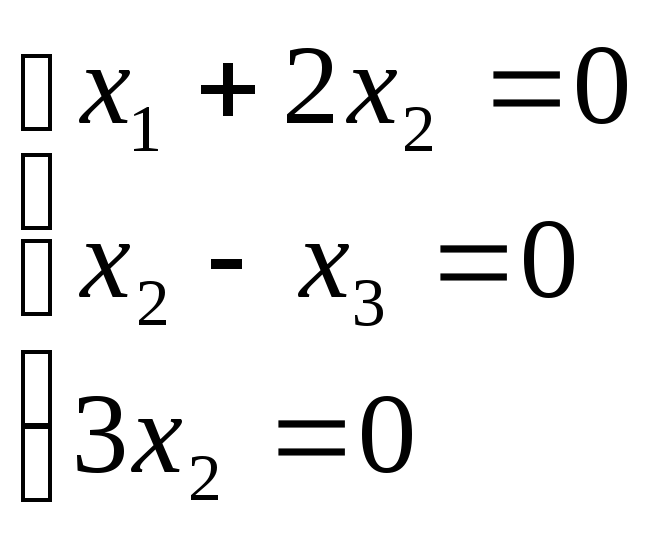
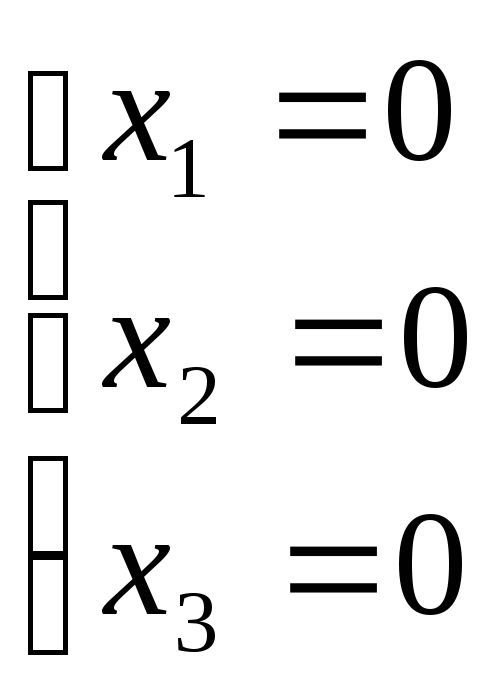
где
-дефект
ядра
Ответ:
,
.
Б2 2.3 Найдите действительные собственные значения и собственные векторы линейного преобраования
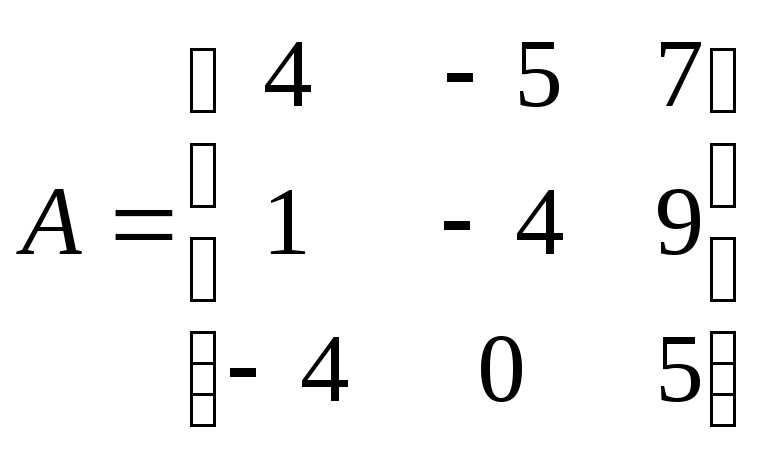
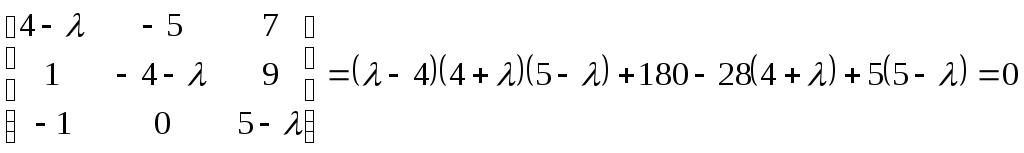
При делении столбиком
многочлена
на многочлен
получим
.
(
)(
)=0
,
,
.
Согласно определению комплексные числа
не яв-ся собств.значения лин.оператора.
только
1)
=
=
=
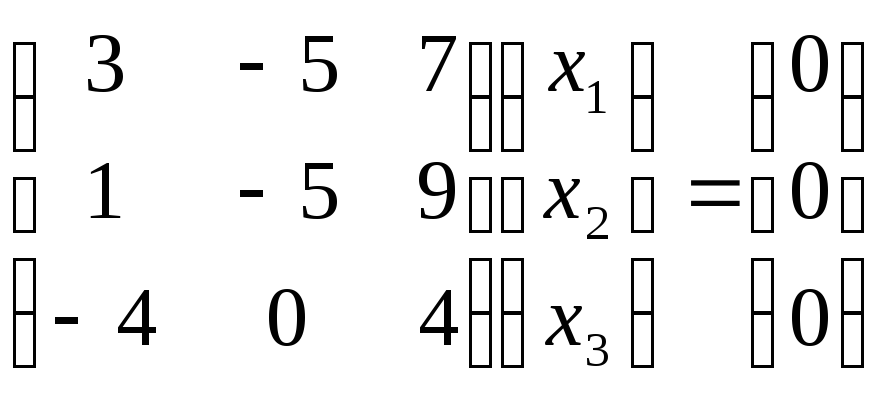
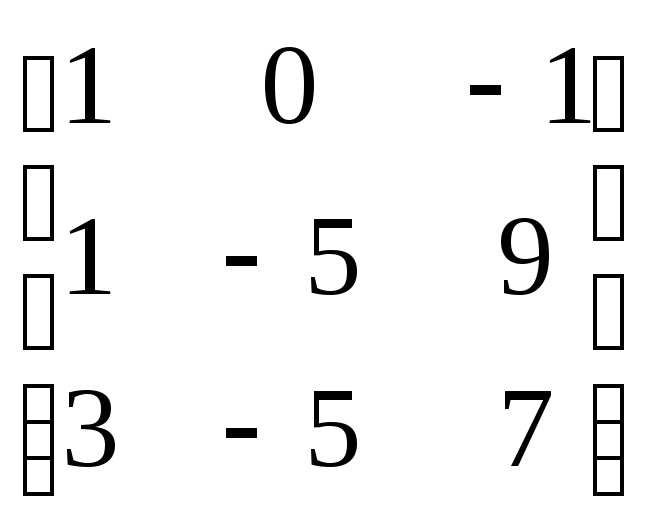