ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.04.2024
Просмотров: 66
Скачиваний: 0
,
ранг
.
Поэтому размерность лин пр-ва решений = 3-2=1.
Фундаментальная
система решений содержит одно решение,
например,
.
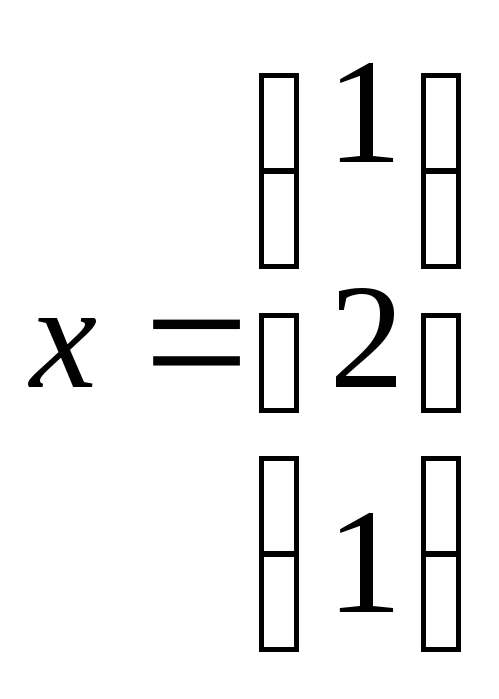Все множество
собственных векторов лин оп-ра с
собств.значениями
в корд форме имеет вид
,
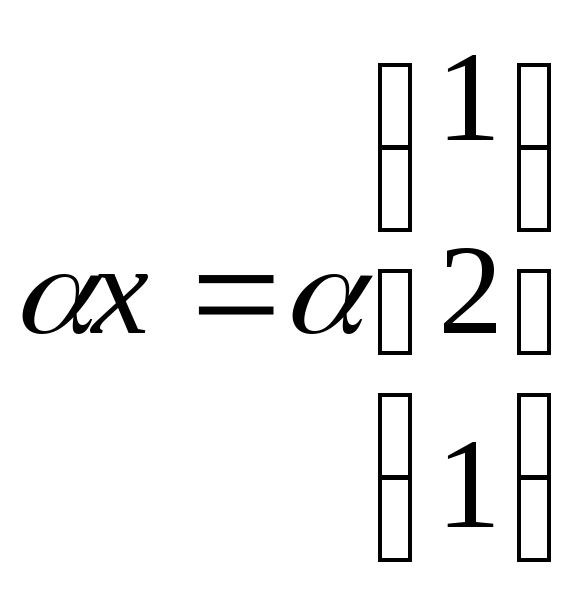где
любое
число
Ответ:
,
,
.
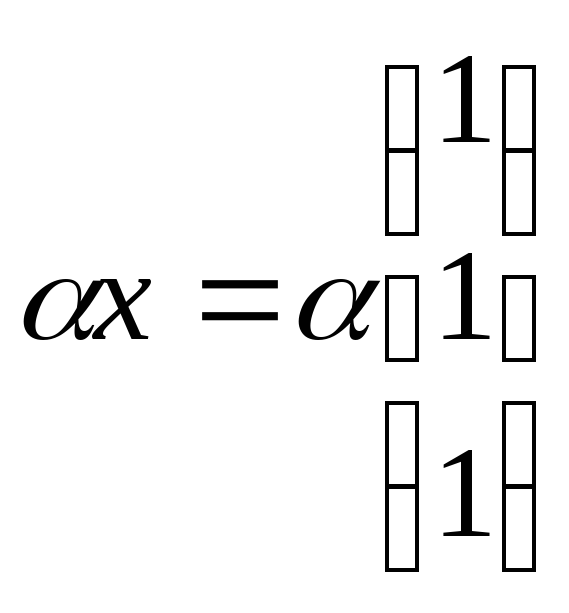Б2 3.1 привести к каноническому виду данную бином форму
Проверим на
симметричность
,
билинейная форма
явл симметричной
По определению :
квадратичная форма - численная ф-ия
одного векторного аргумента
,
полученная из билинейной формы
при
.
В нашем случае
,
.
Имеем
Заменим
,
Имеем канонический
вид
.
Ответ
.
Б2 3.2 Привести
данную квадратичную форму к каноническому
виду с помощью метода Лагранжа. Найти
ранг, положительный и отрицательный
индексы инерции и сигнатуру этой формы:
.
Сделаем замену переменных
Имеем канонический
вид
.
Ранг квадратичной
формы равен числу отличных от 0 коэф-ов
в
ее каноническом виде.
ранг
,
,
.
Сигнатура
- число положит
- чмсло отриц коэф-ов
в нормир виде
- сигнатура
Б2 3.3 Найти ортогон преобразование, привод к канонич виду квадр форму 2х перем:
Теперь можно зап канонич вид
Ответ :
