Файл: курсовая.doc

В открытых интервалах обозначена только одна граница. Открытыми интервалы бывают обычно в первой и последней группах (например, до 10, 10-15, 15-20, 20 и более).

Правила записи числа шага интервала:

- если величина интервала представляет собой величину, которая имеет 1 знак до запятой (например, 0,88; 1,585; 4,71), то полученные значения округляются до десятых (0,9; 1,6; 4,7);

- если 2 знака до запятой и несколько после (например, 15,985), то округляют до целых);

- если 3 знака и более до запятой, то округляют до ближайшего числа, кратного 50 или 100 (например, 557 следует округлить до 600; 112,53 до 100; 148,2 до 150).

Результаты группировок представляются в виде таблиц.

Статистическая таблица - форма наглядного и наибо­лее рационального изложения полученных в результате, ста­тистической сводки и группировки числовых (цифровых) дан­ных.

Подлежащее таблицы - статистическая совокупность, о которой идет речь в таблице, т.е. перечень отдельных, или всех единиц совокупности или их групп.

Сказуемое табли­цы - показатели, с помощью которых дается характеристика явления, отображаемого в таблице.

В простой таблице в подлежащем дается простой пере­чень каких-либо объектов или территориальных единиц, т.е. в подлежащем нет группировки единиц совокупности. Простые таблицы бывают монографическими и перечневыми. Моногра­фические таблицы характеризуют не всю совокупность еди­ниц изучаемого объекта, а только одну какую-либо группу из него, выделенную по определенному, заранее сформирован­ному признаку. Простыми перечневыми таблицами называ­ются таблицы, подлежащее которых содержит перечень еди­ниц изучаемого объекта.

Групповыми называются статистические таблицы, подле­жащее которых содержит группировку единиц совокупности по одному количественному или атрибутивному признаку. Сказу­емое в групповых таблицах состоит из числа показателей, необходимых для характеристики подлежащего.

Комбинационными называются статистические таблицы, подлежащее которых содержит группировку единиц совокуп­ности одновременно по двум и болев признакам: каждая из групп, построенная по одному признаку, разбивается, в свою очередь, на подгруппы по какому-либо другому признаку и т.д.

Основные правила составления статистических таблиц:

1) таблица по возможности должна быть небольшой и легкообозримой. В случае необходимости обработки большого количества материала вместо одной таблицы иногда могут быть построены несколько взаимосвязанных и последовательно расположенных друг за другом таблиц;

---

2) таблица должна содержать следующие компоненты:

- заголовок (в нем обычно указывается объект или территория, которым посвящена таблица);

- время, к которому относятся данные;

- единицы измерения, они могут указываться в заголовке таблицы, если все показатели таблицы выражены в одних и тех же единицах измерения и счета, или в заголовке соответствующих граф в случае присутствия в таблице различных единиц измерения;

3) при заполнении таблиц используются следующие условные обозначения:

- отсутствие данных в случае, если данная позиция не подлежит заполнению, обозначается знаком умножения (х);

- при отсутствии яв­ления ставится знак тире (—);

- при отсутствии данных ставится многоточие (...) или пишется «н. св.» (нет сведений);

- для отображения очень малых чисел используют обозна­чение 0.0 или 0.00;

4) цифровые данные записываются в таблицу с одной и той же степенью точности;

5) сопоставляемую в ходе анализа информацию распола­гают в соседних графах (либо одну под другой);

6) если таблица печатается на нескольких страницах, то на первой странице сразу под сказуемым печатается строка, в которой графы сказуемого нумеруются, а на последующих страницах заголовки граф не повторяются, а указываются только их цифровые обозначения.

Средними величинами в статистике называют обобщающие показатели, выражающие типичные, характерные для определенных условий места и времени размеры и количественные соотношения явлений общественной жизни. В средних величинах погашаются индивидуальные различия в величине признака, которые возникают по тем или иным причинам у отдельных единиц изучаемой совокупности, и, наоборот, определяется уровень варьирующего признака, типичный для большинства единиц данной совокупности.

Статистическая совокупность – совокупность социально-экономических объектов или явлений общественной жиз­ни, объединенных качественной основой, общей связью, но отличающихся друг от друга отдельными признаками.

Вариация — количественные изменения значений призна­ка при переходе от одной единицы совокупности к другой. Вариация возникает под воздействием случайных, прежде всего внешних, причин. Вариация у единиц совокупности означает, что их признаки могут принимать различные значения или видоизменения. Такие признаки называются варьирующими, а отдельные значения или видоизменения называются вариантами.

---

В статистике различают несколько видов средних величин: арифметическую, гармоническую, геометрическую, хронологическую.

Конкретное решение о том, какой вид средней величины надо использовать в каждом отдельном случае, принимается в зависимости от экономического содержания изучаемого явления.

В зависимости от частоты повторения вариант средние исчисляются как простые невзвешенные, так и взвешенные.

Среднюю арифметическую рассчитывают по формуле:

- невзвешенную - взвешенную

где x_i – значение усредняемого признака,

f_i – частота появления признака,

n – единиц совокупности.

Разновидностью средней является мода и медиана. Это так называемые структурные средние, которые применяются для изучения внутреннего строения рядов распределения значений признака. Мода и медиана рассчитываются в дискретных и в интервальных рядах.

Дискретные вариационные ряды основаны на прерывных, или дискретных, признаках, интервальные – чаще всего на непрерывных. Прерывными называются признаки, имеющие определенные значения, между которыми нет промежуточных значений. Непрерывный признак характеризуется тем, что его варианты принимают любое значение. В дискретных рядах варианты выражаются целыми или определенными числами, а в интервальных варианты даются в виде интервалов.

Мода – это значение варьирующего признака (варианта), которое чаще всего встречается в статистическом ряду, т.е. это варианта, которой соответствует наибольшая частота.

В дискретных рядах модой является значение варианты с наибольшей частотой.

В интервальных рядах мода определяется по формуле:

где x_Mo - нижняя граница модального ряда,

i – величина модального интервала,

f_Mo – частота модального ряда,

f_Mo-1 – частота ряда, предшествующего модальному,

f_Mo+1 – частота ряда, следующего за модальным.

Модальный интервал – интервал, имеющий наибольшую частоту.

---

Медиана – это варианта, которая находится в середине непрерывно возрастающего (убывающего) вариационного ряда. Медиана делит ряд пополам, и по обе стороны от нее находится одинаковое количество единиц совокупности.

В дискретных рядах распределения при нечетном числе членов медианой является варианта, находящаяся в середине упорядоченного ряда. При четном числе членов медианой является средняя арифметическая из двух вариант, стоящих в центре ранжированного ряда.

В интервальном вариационном ряду медиана находится следующим образом. Сначала определяется медианный интервал - интервал, в котором находится медиана. Это интервал, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот.

Затем определяется медиана по формуле:

где x_Mе - нижняя граница медианного ряда,

i – величина медианного интервала,

f_Mе – частота медианного интервала,

f_н – сумма накопленных частот в интервалах, предшествующих медианному,

∑f_i – сумма частот.

Недостаточность средней величины для полной характеристики совокупности заставля­ет дополнять средние величины показателями, позволяющи­ми оценить типичность или нетипичность этих средних путем измерения колеб­лемости (вариации) изучаемого признака.

Самыми простыми признаками вариации являются минимум и максимум - это самое наименьшее и наибольшее значение признака в совокупности.

Размах вариации (R) - разность между максимальным (x_max) и минимальным (x_min ) значениями признака в изучаемой совокупности:

R = x _max – x _min

Размах вариации не характеризует распределение отклонения внутри совокупности, он позволяет судить лишь о разбросе край­них значений признака в совокупности, т.е. делать выводы о том, в каких пределах варьируются значения изучаемого при­знака.

Среднее линейное отклонение:

- невзвешенное - взвешенное

---

где │‌‌‌x-x_ср│- абсолютное значение (модуль) отклонения варианты от средней арифметической.

Среднее линейное отклонение характеризует отклонение всех вариант от средней арифметической. Однако это значение не учитывает характера отклонений, которые могут быть или положительные, или отрицательные.

Для более точного определения колебаний численного значения изучаемого признака используются среднее квадратическое отклонение (σ) и дисперсия (σ²).

Дисперсия (σ²) - средняя арифметическая квадратов отклонений ва­риантов значений признака от их средней величины. Дисперсия обычно называется средним квадратом отклонений:

- невзвешенная - взвешенная

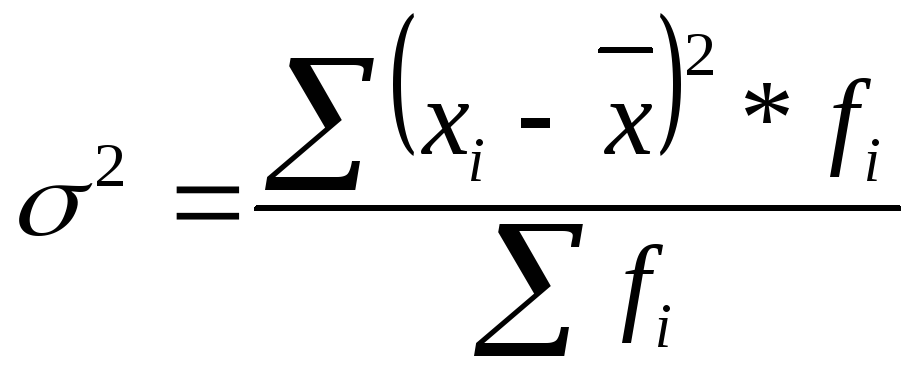
Среднее квадратическое отклонение – это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Среднее квадратическое отклонение всегда выражаются в тех единицах измерения, в которых выражены сами варианты и их средняя.

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:

Если значение среднего квадратического отклонения составляет половину и более значения средней, то данные можно считать неоднородными.

Коэффициент вариации - наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Этот показатель позволяет сопоставить вариацию признака совокупностей, варианты которых имеют различные единицы измерения.

Совокупность считается качественно однородной, а средняя – типичной, если коэффициент вариации не превышает 33%. Коэффициент вари­ации применяется для сравнения колеблемости разнородных признаков.

---