ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.04.2024
Просмотров: 247
Скачиваний: 0
Тема. Ряды динамики Задание 2
Таблица 3. Динамика производства основных продуктов питания
в России на душу населения
|
Год |
Производство, кг |
|||
|
сахара и кондитерских изделий |
овощей |
зерна |
картофеля |
|
|
1985 |
25,4 |
86 |
688 |
236 |
|
1986 |
27,5 |
89 |
744 |
298 |
|
1987 |
27,4 |
87 |
677 |
261 |
|
1988 |
26,8 |
88 |
638 |
229 |
|
1989 |
28,5 |
84 |
710 |
229 |
|
1990 |
24,3 |
77 |
787 |
208 |
|
1991 |
20,9 |
77 |
599 |
231 |
|
1992 |
26,3 |
72 |
717 |
257 |
|
1993 |
26,5 |
67 |
701 |
243 |
|
1994 |
26,2 |
68 |
630 |
258 |
|
1995 |
27,0 |
75 |
428 |
268 |
|
1996 |
26,0 |
79 |
530 |
243 |
|
1997 |
39,0 |
80 |
601 |
252 |
|
1998 |
44,0 |
72 |
326 |
214 |
|
1999 |
57,0 |
84 |
374 |
214 |
|
2000 |
53,4 |
84 |
406 |
222 |
|
2001 |
58,4 |
89 |
507 |
223 |
|
2002 |
57,0 |
88 |
522 |
215 |
Таблица 4. Распределение данных по вариантам для задания 2
|
Номер варианта |
Производство продукции и годы |
Схема расчета |
|
1 |
1985-1990 сахар и кондитерские изделия |
Базисная и цепная схема |
|
2 |
1991-1996 сахар и кондитерские изделия |
Базисная и цепная схема |
|
3 |
1997-2002 сахар и кондитерские изделия |
Базисная и цепная схема |
|
4 |
1985-1990 овощи |
Базисная и цепная схема |
|
5 |
1991-1996 овощи |
Базисная и цепная схема |
|
6 |
1997-2002 овощи |
Базисная и цепная схема |
|
7 |
1985-1990 зерно |
Базисная и цепная схема |
|
8 |
1991-1996 зерно |
Базисная и цепная схема |
|
9 |
1997-2002 картофель |
Базисная и цепная схема |
|
10 |
1985-1990 картофель |
Базисная и цепная схема |
|
11 |
1997-2002 зерно |
Базисная и цепная схема |
|
12 |
1991-1997 картофель |
Базисная и цепная схема |
Согласно своего варианта произвести:
1) расчет показателей анализа рядов динамики;
2) аналитическое выравнивание по прямой;
3) рассчитать прогнозное значение анализируемого показателя на год, следующий за последним.
Изобразить графически эмпирические данные и линию тренда. Сформулировать выводы.
Методические указания к выполнению задания 2
Рядом динамики называется последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
Основными
показателя, характеризующими ряды
динамики являются начальный (![]() ,
конечный (
,
конечный (![]() )
и средний (
)
и средний (![]() )
уровни ряда.
)
уровни ряда.
Способ расчета средней зависит от характера ряда. Выделяют моментные и интервальные ряды динамики. Интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам и т.д. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики. Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.д.
Средняя в рядах динамики, рассчитывается как средняя хронологическая, по следующей формуле:
![]() ,
где
,
где
![]() - сумма значений уровней ряда;
- сумма значений уровней ряда;
n - количество уровней ряда.
Средняя хронологическая, рассчитывается как по моментным, так и по интервальным рядам.
Если ряды имеют разные временные интервалы, то в этом случае рассчитывается средняя как средневзвешенная.
В моментных рядах с равными временными интервалами средняя хронологическая определяется следующим образом:
![]() =
=![]() .
.
Расчет средней в моментных рядах с неравновеликими интервалами ведется также по средневзвешенной.
В экономической практике часто определяют средние уровни ряда моментных величин с неравноотстоящими датами времени. В этом случае средняя рассчитывается по формуле:
![]() =
= ![]() ,
где
,
где
y – значение уровня ряда;
t – длина временного периода.
Другими показателями характеризующими ряды динамики являются темп роста, темп прироста, абсолютный прирост, абсолютное значение 1-го % прироста, коэффициент роста и коэффициент прироста. Данные показатели могут быть рассчитаны по двум схемам: базисной и цепной.
Расчет показателей динамики представлен в следующей таблице:
Таблица 5. Показатели ряда динамики
|
Показатель |
Базисная схема расчета |
Цепная схема расчета |
|
Абсолютный прирост |
|
|
|
Коэффициент роста |
|
|
|
Темп роста |
|
|
|
Коэффициент прироста |
|
|
|
Темп прироста |
|
|
|
Абсолютное значение 1-го % прироста |
- |
А=0,01 |
Уравнение прямой при аналитическом выравнивании ряда динамики имеет следующий вид:
![]()
где
![]() - выровненный (средний) уровень
динамического ряда;
- выровненный (средний) уровень
динамического ряда;
a0, a1 - параметры искомой прямой;
t - условное обозначение времени.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a0 и a1:
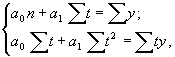
где у - исходный уровень ряда динамики;
n - число членов ряда.
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю, т. е. начало времени перенести в середину рассматриваемого периода.
Если
![]()
то
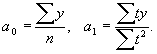
Исследование динамики социально-экономических явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) - определения будущих размеров уровня экономического явления.