Файл: Тема 12.doc

Индекс цен определяется по следующей формуле:

,

(12.15)

где в числителе дроби - фактическая стоимость продукции текущего периода, а в знаменателе - условная стоимость тех же товаров в це­нах базисного периода.

Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за изменения цен, или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен. Если из значения индекса (12.15) вычесть 100% (), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции из-за изменения цен, а разность числителя и знаменателя () - на сколько рублей изменилась стоимость продукции в результате роста (снижения) цен. Изменение количества произведенной продукции в текущем периоде по сравнению с базисным не влияет на величину индекса.

Пример.Определим индекс цен по данным табл. 12.1:

, или 119,50%.

Таким образом, в среднем по трем товарам цены выросли в 1,195 раза (или рост цен составил 119,5%). В результате увеличения цен на 19,5%о (119,5% - 100% = 19,5%) покупатели заплатили на 46,7 тыс. руб. больше в феврале, чем в январе (286,2 - 239,5 = 46,7 тыс. руб.).

Как уже отмечалось выше, стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связь существует и между индексами стоимости, физического объема и цен, т.е.:

(12.16)

или

.

(12.17)

Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора. Алгебраическая сумма этих разностей равна разности числителя и знаменателя индекса стоимости продукции:

---

.

(12.18)

Равенства (12.16-12.18) выполняются в том случае, если при исчислении индекса объемного показателя веса были зафиксированы на уровне базисного периода, а при расчете индекса качественного показателя - на уровне отчетного периода.

Пример.Для нашего примера (см. табл. 12.1) индекс стоимости, исчисленный по формуле (12,16), равен;

1,0659 * 1,1950 = 1,274, или 127,4%,

а алгебраическая сумма этих разностей, определенная по формуле (12.18), равна:

14,8 + 46,7 = 61,5 тыс. руб.

Формулы для расчета обших индексов других показателей приведены в табл. 12,2.

Таблица 12.2
Основные формулы исчисления сводных, или общих, индексов
Наименование	Формула расчета	Что показывает индекс	Что показывает значение индекса, уменьшенное на 100%, т.е.	Что показывает разность числителя и знаменателя
Индекс физического объема продукции		Во сколько раз изменилась стоимость продукции в результате изменения ее объема, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения ее физического объема	На сколько процентов изменилась стоимость продукции в результате изменения ее объема	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) ее объема
Индекс цен		Во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен	На сколько процентов изменилась стоимость продукции в результате изменения цен	На сколько рублей изменилась стоимость продукции в результате роста (уменьшения) цен
Индекс стоимости продукции (товаро­оборота)		Во сколько раз возросла (уменьшилась) стоимость продукции, или сколько процентов составил рост (снижение) стоимости продукции в текущем периоде по сравнению с базисным	На сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным	На сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным
Индекс физического объема		Во сколько раз изменились издержки производства продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения физического объема ее производства	На сколько процентов изменились издержки производства продукции в результате изменения объема ее производства	На сколько рублей изменились издержки производства продукции в результате роста (уменьшения) объема ее производства
Индекс себестоимости продукции		Во сколько раз изменились издержки производства продукции в результате изменения себестоимости продукции, или сколько процентов составил рост (снижение) издержек производства продукции из-за изменения ее себестоимости	На сколько процентов изменились издержки производства продукции в результате изменения ее себестоимости	На сколько рублей изменились издержки производства в результате роста (уменьшения) себестоимости продукции
Индекс издержек производства		Во сколько раз возросли (уменьшились) издержки производства продукции, или сколько процентов составил рост (снижение) издержек производства продукции в текущем периоде по сравнению с базисным	На сколько процентов возросли (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным	На сколько рублей увеличились (уменьшились) издержки производства продукции в текущем периоде по сравнению с базисным
Индекс физического объема продукции		Во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства, или сколько процентов составил рост (снижение) затрат времени на производство продукции из-за изменения физического объема ее производства	На сколько процентов изменились затраты времени на производство продукции в результате изменения объема ее производства	На сколько человеко-часов возросли (уменьшились) затраты времени на производство продукции в результате роста (уменьшения) объема производства продукции
Индекс производительности труда по трудовым затратам		Во сколько раз увеличилась (уменьшилась) производительность труда, или сколько процентов составило снижение (рост) производительности труда в текущем периоде по сравнению с базисным	На сколько процентов изменилась производительность труда в текущем периоде по сравнению с базисным	Абсолютный размер экономии (перерасхода) затрат живого труда в связи с ростом (уменьшением) его производительности
Индекс затрат времени на производство продукции		Во сколько раз изменились затраты времени на производство продукции, или сколько процентов составил рост (снижение) затрат времени на производство продукции в текущем периоде по сравнению с базисным	На сколько процентов изменились затраты времени на производство продукции в текущем периоде по сравнению с базисным	На сколько человеко-часов увеличились (уменьшились) затраты на производство продукции в текущем периоде по сравнению с базисным

---

12.4

---

Средние индексы

Помимо агрегатных индексов в статистике применяется другая их форма - средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то общий индексцеп как агрегатный определить нельзя, однако возможно исчислить его как средний из индивидуальных. Точно так же, если не известны количества произведенных отдельных видов продукции, но известны индивидуальныеиндексы и стоимость продукции базисного периода, то можно определитьобщий индекс физического объема продукции как средневзвешенную величину.

Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов. Агрегатный индекс является основной формойобщего индекса, поэтому средний индекс должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.

Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу.

Средний арифметический индекс физического объема продукции вычисляется по формуле:

.

(12.19)

Так как , то формула этого индекса легко преобразуется в форму (12.14). Весами в формуле (12.19) является стоимость продукции базисного периода.

Средний арифметический индекс производительности труда определяется следующим образом:

.

(12.20)

Так как то формула этого индекса может быть преобразована в агрегатный индекс трудоемкости продукции. Весами являются общие затраты времени на производство продукции в текущем периоде.

---

В статистике широко известен и другой средний арифметический индекс, который используется при анализе производительности труда. Он носит название индекса Струмилина и определяется следующим образом:

.

(12.21)

Индекс показывает, во сколько раз возросла (уменьшилась) производительность труда, или сколько процентов составил рост (снижение) производительности труда в среднем по всем единицам исследуемой совокупности.

Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. При анализе качественных показателей данная форма индекса применяется для исчисления приведенных выше индексов (формулы (12.20)-(12.21)).

Индексы других качественных показателей (цен, себестоимости и т.д.) определяются по формуле средней гармонической взвешенной величины.

Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числите­ля агрегатного индекса.

Например, индекс себестоимости можно исчислить так:

,

(12.22)

а индекс цен:

.

(12.23)

Таким образом, при определении среднего гармонического индекса себестоимости весами являются издержки производства текущего периода, а при вычислении индекса цен веса - стоимость продукции этого периода.

Рассчитаем средние индексы цен и физического объема продукции по данным табл. 12.1 (графы 11-12):

, или 106,59%;

, или 119,50%.

Этот же результат получился при расчете агрегатных индексов. Средние индексы широко используются для анализа рынка ценных бумаг. Наиболее известными являются индексы Доу-Джонса, Стэндарда и Пура.

Индекс Доу-Джонса (DowJonesIndustrialAverageIndex) определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется их значение на момент закрытия биржи. Групповые индексы определяются по ценам акций 30 промышленных, 20 транспортных и 15 компаний сферы услуг. Общий индекс рассчитывается по всем 65 компаниям. Их перечень был составлен в 1928 г. В качестве базисного выбран 1920 г. Первоначальная методика исчисления индекса была разработана основателем и редактором крупнейшей в США газеты «Уолл-стрит джорнел» Чарлзом Доу.

---
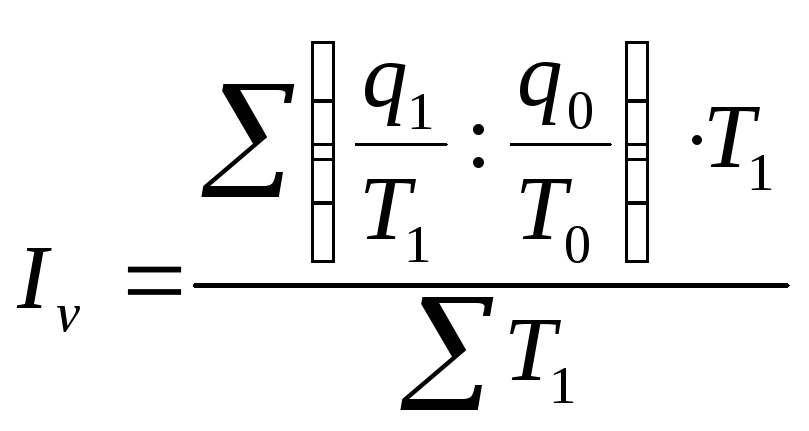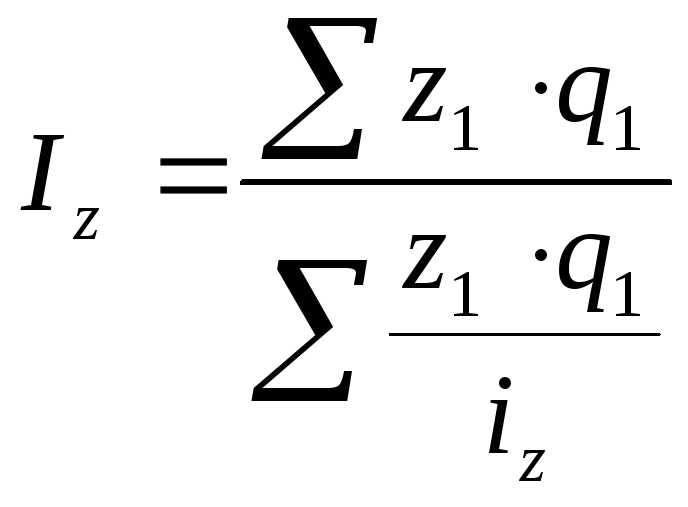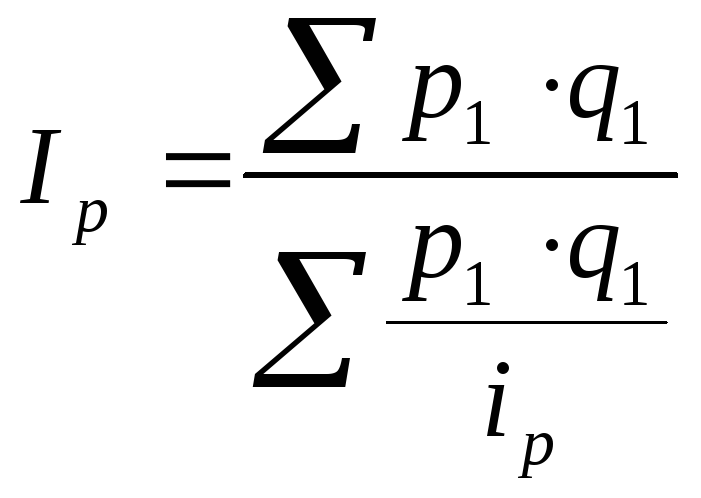