Файл: Тема 12.doc

Индексы структурных сдвигов

При изучении динамики качественных показателей приходится определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов - изменением значения индексируемого показателя у отдельных групп единиц и измене­нием структуры явления. Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности. Так, средняя заработная плата на предприятии может вырасти в результате роста оплаты труда работников или увеличения доли высокооплачиваемых сотрудников. Снижение трудоемкости производ­ства единицы продукции по совокупности предприятий отрасли может быть обусловлено повышением производительности труда на предприятиях или концентрацией производства продукции на заводах с низкой трудоемкостью. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определить степень влияния каждого из факторов на обитую динамику средней.

Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:

,

(12.32)

где

индекс переменного состава.

Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов).

Индекс постоянного (фиксированного) состава - это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксированного состава определяется как агрегатный индекс, Так, индекс фиксированного состава себестоимости продукции рассчитывают по формуле:

---

,

(12.33)

где

индекс фиксированного состава.

Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):

,

(12.34)

где

индекс структурных сдвигов.

Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:

(12.35)

Рассмотрим применение такой системы.

Пример.Пусть имеются данные об объеме строительства коттеджей и себестоимости 1 кв. м. жилья двух строительных фирм в мае-июне 2002 г. (табл. 12.4).

В июне по сравнению с маем 2002 г. себестоимость 1 кв. м. коттеджного жилья в двух строительных фирмах возросла: в ООО «Скат» она увеличилась на 5,26%, а в ООО «Стройинвест» - на 16,67%. При этом изменилась структура рынка участников строительства: уменьшилась доля первой строительной фирмы (ООО «Скат») в общем объеме строительства коттеджей (с 35,1 до 28,5%) и возросла доля второй фирмы (ООО «Стройинвест») - с 64,9 до 71,5%).

Рассчитаем индекс переменного состава. Для этого сначала определим среднюю себестоимость единицы продукции в текущем и базисном периодах:

, или 294,7 долл. США.

, или 335,8 долл. США.

---

Тогда

, или 113,5%.

Следовательно, средняя себестоимость по двум фирмам возросла в текущем периоде по сравнению с базисным на 13,95%, и в каждом из них в отдельности она возрастала. Это результат того, что исчисленный индекс учитывает влияние еще и структурного фактора.

Определим индекс себестоимости фиксированного состава:

, или 113,5%.

Таким образом, себестоимость в текущем периоде по сравнению с базисным возросла в среднем на 13,5%.

Вычислим влияние изменения структуры на динамику средней себестоимости:

, или100,34%.

Изменение доли строительных фирм в общем объеме построенного коттеджного жилья привело к увеличению себестоимости на 0,34%.

Таблица 12.4
Построено коттеджного жилья и себестоимость 1 кв. м по двум строительным фирмам в мае-июне 2002 г.*
Строительная фирма	Построено коттеджного жилья				Себестоимость единицы продукции, долл. США		Индивидуальные индексы себестоимости, %	Общие затраты на производство жилья, тыс. долл. США
	Всего, кв. м.		% к итогу		Базисный период (май)	Текущий период (июнь)		Базисный период (май)	Текущий период (июнь)
	Базисный период (май)	Текущий период (июнь)	Базисный период (май)	Текущий период (июнь)
А	1	2	3	4	5	6	7 = 6:5	8 = 5 · 1	9 = 6 · 2	10 = 5 · 2
ООО «Скат»	1620	1780	35,1	28,5	285	300	105,26	461,7 900,0	534,0 1564,5	507,3 1341,0
ООО «Стройинвест»	3000	4470	64,9	71,5	300	350	116,67
Итого	4620	6250	100,0	100,0	-	-	-	1361,7	2098,5	1848,3
* Цифры условные.

---

Аналогично строятся системы индексов для других показателей. Так, для показателя производительности труда можно построить систему индексов, в которой:

;	(12.36)
;	(12.37)
,	(12.38)

12.7

---

Индексы пространственно-территориального сопоставления

В статистической практике часто возникает потребность в сопоставлении уровней экономического явления в пространстве: по странам, экономическим районам, областям, т.е. в исчислении территориальных индексов. При построении территориальных индексов приходится решать вопрос, какие веса использовать при их исчислении. Например, если стоит задача сравнить цены двух регионов (А и Б), то можно построить два индекса:

(12.39)

и

,

(12.40)

где		индекс, в котором в качестве базы сравнения применяются данные по региону А.
		индекс, используемый в качестве базы сравнения данных по региону Б.

Эти формулы могут дать совершенно различное представление о соотношении уровней явления. Например, при расчете по формуле 12.39) значение признака будет ниже в регионе А, а по формуле 12.40) - в регионеБ.

Пример.Рассмотрим табл. 12.5.

Рассчитав индексы по двум формулам, получаем:

, или97,3%

и

, или 102,9%

Индексы показывают, что при сравнении региона А с региономБ цены ниже в регионеА на 2,7%, а при сравнении регионаБ с региономА оказывается, что цены несколько выше в регионеБ. Таким образом, расчет индексов не позволяет определить, в каком регионе выше цены. Причина заключается в резком различии структуры продаж в отдельных регионах.

---
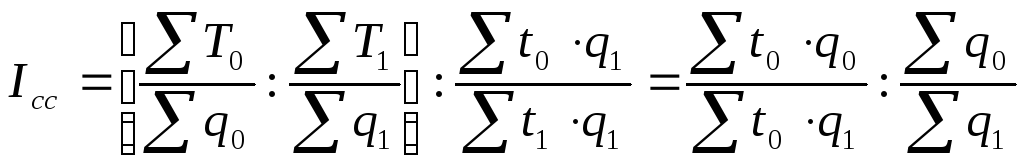