ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 01.08.2024
Просмотров: 113
Скачиваний: 0
Рассмотрим более подробно свойства индексов Ласпейреса и Пааше. Для удобства изложения введем следующие обозначения:
|
|
|
|
|
|
Свойство 1:
|
|
(12.54) |
т.е. индекс цен в формуле Пааше равен отношению индекса стоимости продукции к индексу физического объема в формуле Ласпейреса.
Свойство 2:
|
|
(12.55) |
или
|
|
(12.56) |
Данное свойство позволяет сократить
объем вычислительной работы. Действительно,
для определения индекса цен и физического
объема необходимо иметь две величины
условной стоимости:
![]() и
и![]() Если рассчитать величину базисного
объема товаров в текущих ценах (
Если рассчитать величину базисного
объема товаров в текущих ценах (![]() ),
то можно исчислить сначала индекс цен
по формуле Ласпейреса (
),
то можно исчислить сначала индекс цен
по формуле Ласпейреса (![]() ),
а затем, разделив этот индекс на индекс
стоимости (
),
а затем, разделив этот индекс на индекс
стоимости (![]() ),
получить индекс физического объема по
формуле Пааше (
),
получить индекс физического объема по
формуле Пааше (![]() ).
).
Свойство 3:
|
|
(12.57) |
Если имеются индивидуальные индексы
цен, то индекс цен по формуле Ласпейреса
может быть исчислен как средняя
арифметическая величина, где в качестве
весов используется стоимость продукции
базисного периода (![]() ).
Именно этот способ определения индекса
цен наиболее часто используется на
практике зарубежными статистиками.
).
Именно этот способ определения индекса
цен наиболее часто используется на
практике зарубежными статистиками.
Свойство 4:
|
|
(12.58) |
Индекс физического объема по формуле
Ласпейреса - это средняя арифметическая
величина из индивидуальных индексов
объема (![]() ),
взвешенных по стоимости базисного
периода (
),
взвешенных по стоимости базисного
периода (![]() ).
).
Свойство 5:
|
|
(12.59) |
В данном случае в качестве весов
используется условная стоимость - (![]() )
)
Свойство 6:
|
|
(12.60) |
Весами служит стоимость продукции
базисного периода, исчисленная в ценах
отчетного периода (![]() ).
).
При взвешивании индекса по величине
стоимости продукции базисного периода
(![]() )
возникает постоянная погрешность,
причиной которой является тот факт, что
цена входит как сомножитель в веса и
между изменениями цен весов существует
корреляция:
)
возникает постоянная погрешность,
причиной которой является тот факт, что
цена входит как сомножитель в веса и
между изменениями цен весов существует
корреляция:
|
|
(12.61) |
|
где |
|
|
|
|
|
|
|
|
|
|
Так как коэффициенты вариации всегда положительны, а величина коэффициента корреляции между изменениями цен и физического объема на товарном рынке обычно отрицательна, то значение индекса по формуле Пааше всегда меньше значения индекса по формуле Ласпейреса.
12.10
Идеальный индекс фишера
Индекс цен американского экономиста И. Фишера представляет собой среднюю геометрическую из произведения двух агрегатных индексов цен Ласпейреса и Пааше:
|
|
(12.62) |
Формула, предложенная Фишером, может быть использована и для определения индекса физического объема:
|
|
(12.63) |
Геометрическая форма индексов имеет принципиальный недостаток: она лишена конкретного экономического содержания. Так, в отличие от агрегатного индекса Ласпейреса или Пааше, разность между числителем и знаменателем не покажет никакой реальной экономии (или потерь) из-за изменения цен или физического объема продукции.
И Фишер назвал эту формулу расчета индекса идеальной формулой. Идеальность формулы заключается, прежде всего, в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов получается «обратный» индекс, т.е. величина, обратная величине первоначального индекса. Этому условию отвечает любой индивидуальный индекс. Например, индекс цен равен:
![]() ,
,
тогда обратный индекс цен определяется следующим образом:
![]() .
.
Если перемножить эти два индекса, то получится 1:
![]()
Этому условию удовлетворяет идеальный индекс цен Фишера:
|
|
(12.64) |
Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно редко. Чаще всего он применяется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят
12.11
Индексы-дефляторы
Пересчет важнейших стоимостных показателей системы национальных счетов (национальный доход, валовой национальный продукт и т.д.) из фактических цен в сопоставимые осуществляется с помощью индекса-дефлятора. Дефлятор - это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного. Например, индекс-дефлятор валового внутреннего продукта (ВВП) представляет собой индекс цен, применяемый для корректировки номинального объема ВВП с учетом инфляции и получения на этой основе реального его объема1.
Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости продукции, структура которой аналогична структуре отчетного года, но определенная в ценах базисного года. В основе расчета индекса-дефлятора лежит формула Пааше - агрегатная формула индекса с текущими весами. Индекс-дефлятор для ВВП в 2001 г. определяется по формуле:
|
|
(12.65) |
|
где |
|
|
|
|
|
|
|
|
|
|
Реальный ВВП за 2001 г. определяется по формуле:
|
|
(12.66) |
|
где |
|
|
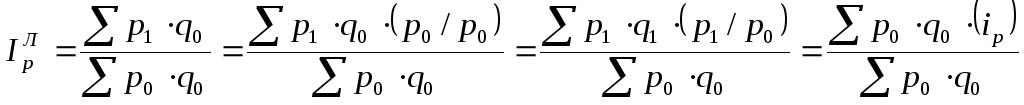 .
.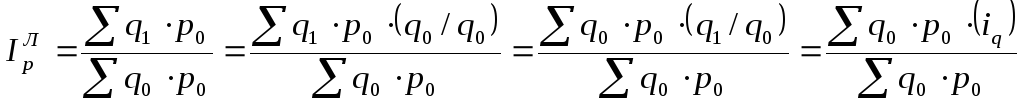 .
.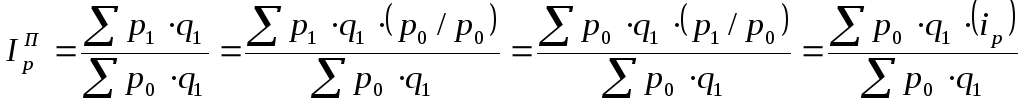 .
.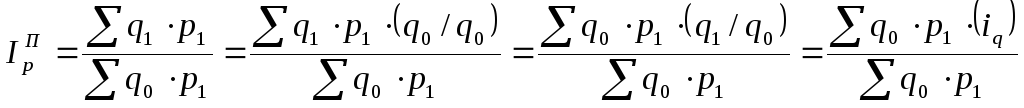 .
.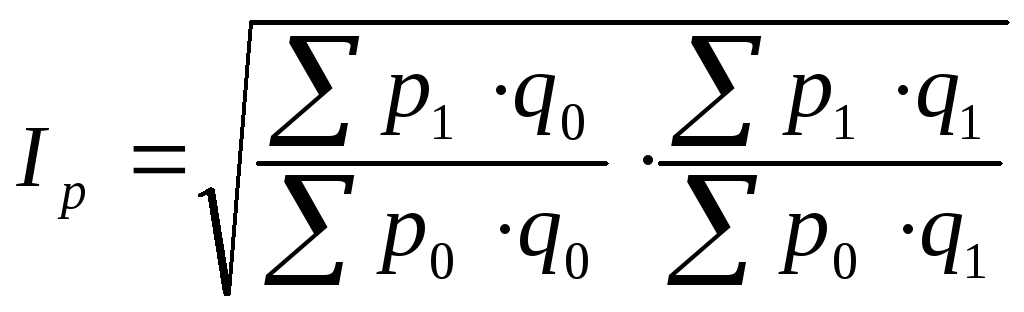 .
.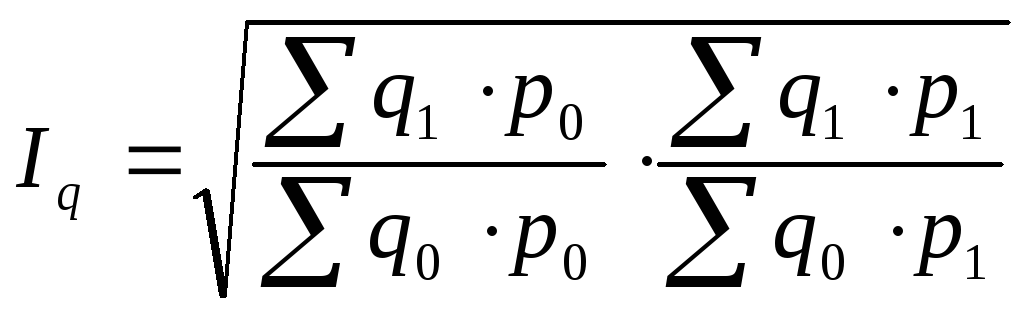 .
.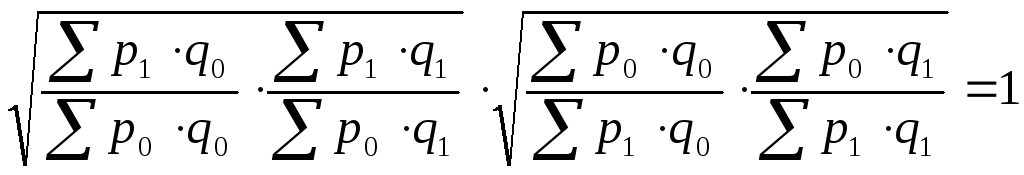 .
.