Файл: Тема 12.doc

В теории и практике статистики предлагаются различные методы построения территориальных индексов, в том числе метод стандартных весов. Этот метод заключается в том, что значения индексируемой величины взвешиваются не по весам какого-то одного региона, а по весам области, экономического района, республики, в которых находятся сравниваемые регионы.

В нашем примере в качестве весов можно использовать количество продукции, проданной в регионах А иБ, т.е.:

.

(12.41)

Таблица 12.5
Цена а продукты питания и количество проданной продукции по двум регионам*
Наименование продукта	Регион А		Регион Б		Товарооборот				Количество продукции, проданной в регионах АиБ
	Цена, руб.,	Количество проданного товара,	Цена, руб.	Количество проданного товара,	Регион А	Регион Б
А	1	2	3	4	5 = 1 · 2	6 = 3 · 4	7 = 3 · 2	8 = 1 · 4	9 = 2 + 4	10=1 · 9	11=3 · 9
Мясо и птица, кг.	95	1700	100	1200	161500	120000	170000	114000	2900	275500	290000
Масло животное, кг	83	800	80	600	66400	48000	64000	49800	1400	116200	112000
Яйца, десяток	17	500	18	1000	8500	18000	9000	17000	1500	25500	27000
Итого	-	3000	-	2800	236400	186000	243000	180800	-	417200	429000
* Цифры условные.

---

Определим значение индекса по данным табл. 12.5:

, или 97,25%.

Итак, цены в регионе А ниже, чем цены в регионеБ, в среднем на 2,75%.

12.8

---

Важнейшие экономические индексы и их взаимосвязи

Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получить другие. Зная, например, значение цепных индексов за какой-либо период времени, можно рассчитать базисные индексы. И наоборот, если известны базисные индексы, то путем деления одного из них на другой можно получить цепные индексы.

Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например связь между индексом стоимости продукции, физического объема продукции и цен (раздел 12.7). Другие индексы также связаны между собой. Так, индекс издержек производства - это произведение индекса себестоимости продукции и индекса физического объема продукции:

.

(12.42)

или

.

(12.43)

Отсюда если себестоимость увеличилась на 10%, а количество продукции снизилось на 8%, то индекс издержек на производство будет равен:

1,10 · 0,92 = 1,012, или 101,2%.

Индекс затрат времени на производство продукции может быть получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемкости, т.е. индекс производительности труда

(12.44)

или

.

(12.45)

При увеличении физического объема продукции в текущем периоде на 15% по сравнению с базисным производительность снизилась на 18%, поэтому индекс затрат времени на производство продукции будет равен:

1,15 : 0,82 = 1,402, или 140,2%.

Существует важная взаимосвязь между индексами физического объема продукции и индексами производительности труда.

---

Индекс производительности труда рассчитывается на основе следующей формулы:

,

(12.46)

т.е. представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах.

Индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых):

.

(12.47)

Таким образом, если численность рабочих возросла на 12%, а производительность труда - на 7%, то индекс физического объема продукции будет равен:

1,12 - 1,07 = 1,20, или 120%.

Взаимосвязь между отдельными индексами может быть использована для выявления влияния отдельных факторов, оказывающих воздействие на изучаемое явление.

Пример.Пусть имеются следующие данные (табл. 12.6).

Таблица 12.6
Динамика отгруженной продукции, численности рабочих и производительности труда на предприятии в мае 2002 г.*
Наименование показателя	Значение показателя в периоде		Абсолютное изменение	Относительная величина динамики, %
	базисном	текущем
А	1	2	3=2-1	4 = 2 : 1 · 100
Стоимость отгруженной продукции, млн. руб.	450	610	+160	136
Численность рабочих, чел.	700	730	+30	104,3
Выработка продукции на одного рабочего, тыс. руб.	642,3	835,6	+193,3	130,1
*Цифры условные.

---

Из табл. 12.6 следует, что численность рабочих увеличилась на 4,3% (730 : 700 = 1,043, или 104,3%); производительность труда - на 30,1% (835,6 : 642,3 = 1,301, или 130,1%), а отгруженная продукция - на 36% (610 : 450 = 1,36, или 1,043 · 1,301 = 1,36, т. е. 136%).

Объем отгруженной продукции в текущем периоде по сравнению с базисным возрос на 160 млн. руб. Это изменение является результатом роста численности рабочих и выработки продукции.

Для того чтобы определить влияние каждого из факторов, введем следующие обозначения. Обозначим численность рабочих через «»,aдругой фактор - выработку продукции на одного рабочего - через «». Тогда стоимость отгруженной продукции - это, а индекс стоимости продукции - это произведение индекса численности занятых на ин­декс производительности труда:

.

(12.48)

Чтобы выявить влияние каждого фактора на общее изменение стоимости отгруженной продукции, необходимо определить динамику одного из факторов, оставив значение другого неизменным. Тогда индекс (12.48) можно представить в двух вариантах:

1. ;	(12.49)
2. .	(12.50)

Каждый из индексов-сомножителей (12.49 - 12.50) отражает влияние одного фактора на изменение стоимости отгруженной продукции при неизменном (базисном или отчетном) уровне другого фактора. Только в 1-м варианте изменение выработки продукции () определяется при численности занятых в текущем периоде, а во 2-м варианте - в базисном периоде. И наоборот, изменение численности занятых () в 1-м 1 варианте определяется при базисном значении выработки продукции, а во 2-м варианте - при текущем его значении.

Рассчитаем влияние каждого из факторов по формуле (12.49):

---
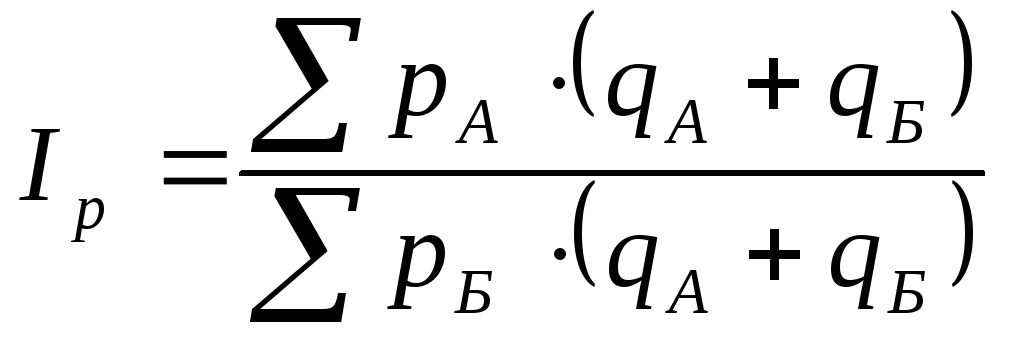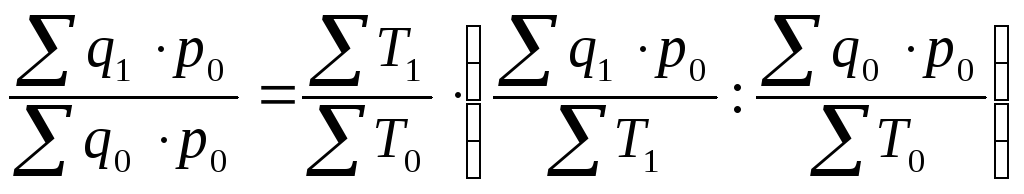