ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 113
Скачиваний: 0
СОДЕРЖАНИЕ
Электромагнитные взаимодействия заряженных частиц
Способ классификации э/м взаимодействий
3. Среда наполнена атомами, атомные оболочки заполнены электронами (z – электронов на атом).
Почему релятивизм не проявился в коэффициенте перед логарифмом в формуле?
напр. рассеяния.)
![]()
Полная вероятность процесса равна квадрату модуля суммарной амплитуды для всех возможных диаграмм.
Диаграммы содержат алгоритм расчета амплитуды процесса.
Амплитуды вероятности единичного испускания (поглощения) частицы, которое происходит в результате определенного взаимодействия, пропорциональна константе g, которая равна корню из константы связи.
Для электромагнитного взаимодействия соответствующая константа равна корню квадратному из постоянной тонкой структуры
gэл(константа связи) =
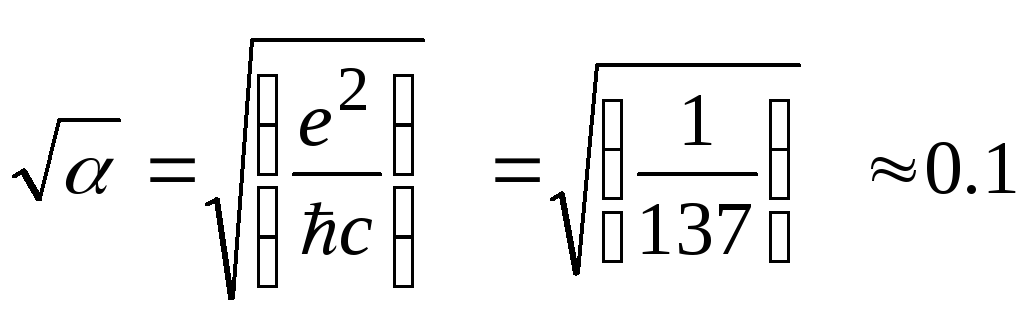 .
.
Для диаграмм с N узлами амплитуда пропорциональна gN.
Вероятность (сечение) процесса пропорциональна квадрату амплитуды.
![]() ,
или
,
или
![]() .
.
![]()
Если в Э/М процессе участвует один фотон (или одна вершина), то вероятность такого процесса пропорциональна ,
![]()
если два фотона (или две вершины) вероятность такого процесса пропорциональна - 2 :
![]()
ПРИМЕР: Оценить отношение сечений двух- и трехфотонной аннигиляции электрон-позитронной пары.

В случае двухфотонной аннигиляции
фейнмановская диаграмма имеет две
вершины, поэтому сечение этого процесса
можно оценить так - ![]()
В случае трехфотонной аннигиляции
фейнмановская диаграмма имеет три
вершины, и сечение этого процесса
пропорционально
![]()
То есть отношение сечений
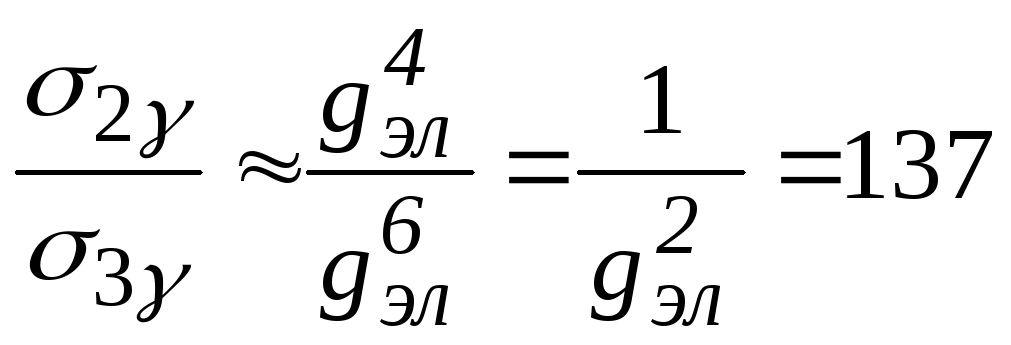
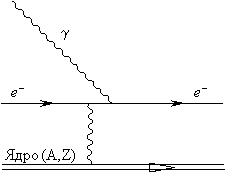
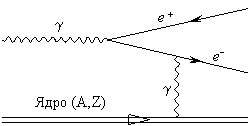
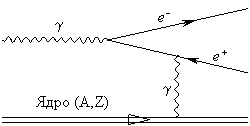
ПРИМЕР: Нарисовать диаграммы Фейнмана для следующих процессов: 1) рассеяние электрона на электроне; 2) эффект Комптона; 3) электрон-позитронная аннигиляция; 4) фотоэффект в кулоновском поле ядра; 5) образование электрон- позитронной пары в кулоновском поле ядра.
1) Рассеяние электрона на электроне. Виртуальная частица - фотон.

2) Эффект Комптона. Виртуальная частица - электрон.
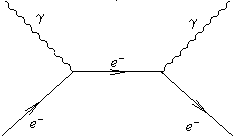

3) Электрон-позитронная аннигиляция. Виртуальная частица - электрон или позитрон.
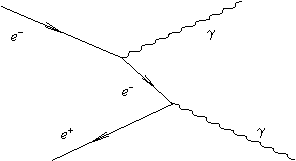

4) Тормозное излучения электрона в поле ядра
5) Фотоэффект в кулоновском поле ядра. Виртуальная частица - фотон.
6) Образование электрон-позитронной пары в кулоновском поле ядра. Виртуальная частица - фотон.
Особый класс взаимодействий составляют процессы, излучения Э/М волн при равномерном движении частиц в среде с показателем преломления n > 1 -- излучение Вавилова-Черенкова. (ИЗЛУЧАЕТ СРЕДА)
Кроме того, существует переходное излучение, возникающее при пересечении равномерно двигающейся заряженной частицы границы раздела двух сред с разными показателями преломления.
Простейшие задачи и оценки.
Задача 1. На основании простейшей концепции Нильса Бора оценить скорости «вращения» электронов в атоме и радиусы электронных орбит.
Ответы:
![]()
![]() .
Т.е. скорость «вращения» электронов в
атоме убывает с увеличением главного
квантового числа n , а
радиус орбиты вращения электронов в
атоме пропорционален n2.
.
Т.е. скорость «вращения» электронов в
атоме убывает с увеличением главного
квантового числа n , а
радиус орбиты вращения электронов в
атоме пропорционален n2.
Задача 2. Найти энергию связи электрона в атоме св .
Ответ. Энергия связи электрона с ядром св , т.е. потенциальная энергия электрона на орбите равна
![]() , а
, а
![]() 2
=
2
=
![]() .
.
В общем случае для электронных орбит в атомах имеем:
![]() и
и
![]() .
.
Чтобы произошла ионизация, т.е.электрон мог покинуть атом, надо, чтобы при взаимодействии
с пролетающей мимо заряженно частицей этот электрон получил кинетическую энергию Те большую, чем энергия связи его с атомом, т.е. Те > cв.
Задача 3. Определить минимальную кинетическую энергию Е и скорость V пролетающей частицы, необходимую для ионизации атома среды.
Ответ. Е
![]() и
и
![]() .
.
Если энергия, передаваемая электрону Те много больше энергии связи этого электрона cв
(Те >> cв)
, т.е. энергия пролетающей частицы Е
![]() ,
то электроны атома можно рассматривать
как свободные и покоящиеся по сравнению
с летящей частицей.
,
то электроны атома можно рассматривать
как свободные и покоящиеся по сравнению
с летящей частицей.
Элементарные электромагнитные процессы можно классифицировать с точки зрения классической физики на основе представлений о параметре удара (прицельном параметре, параметре соударения) b , т.е. расстоянии наибольшего сближения частиц.
При взаимодействии частиц с атомами среды имеет смысл проводить сопоставление параметра удара b с размером атома a.
В зависимости от того, как соотносятся между собой величины b и a происходит тот или иной процесс взаимодействия.
Способ классификации э/м взаимодействий
|
|
b >> a атом вещества реагирует как целое |
b a вз-ие с отдельными электронами атома (электроны атома можно считать отно-сительно свободными) |
b << a вз-ие с кулоновским полем ядра атома |
|
заряженная частица
|
возбуждение и ионизация атома |
значительная (по срав-нению с энергией свя-зи) передача энергии отдельному электрону - - электрон |
Сильное ускорение (или замедление) , искривление траектории частицы, тормозное излучение.
|
|
фотон |
фотоэффект
|
комтоновское рассеяние (комптон-эффект) |
рождение электронно-позитронных пар е+ е- , (*) |
* Заряженные частицы тоже могут образовывать е+ е- пары, так как электромагнитное поле быстро движущейся частицы может быть представлено как поток фотонов со спектром, зависящим от энергии частицы. Эти виртуальные фотоны могут создавать е+ е- пары так же, как и реальные фотоны. Однако, вероятность такого события в 137 раз меньше вероятности рождения пары реальным фотоном.
Взаимодействие тяжелых заряженных частиц со средой
Ионизационные потери тяжелых заряженных частиц.
Элементарные оценки потерь энергии заряженной частицей.
Рассмотрим прохождение через вещество
тяжелой (M >> me)
нерелятивистской ( V<<
c) заряженной (ze)
частицы. Предположим, что эта частица
имеет достаточно высокую скорость (![]() )
, чтобы считать все атомные электроны
свободными.
Итак:
тяжёлая нерелятивистская заряженная
частица с зарядом ze и
скоростью v, пролетает вдоль оси x на
расстоянии b от электрона.
)
, чтобы считать все атомные электроны
свободными.
Итак:
тяжёлая нерелятивистская заряженная
частица с зарядом ze и
скоростью v, пролетает вдоль оси x на
расстоянии b от электрона.
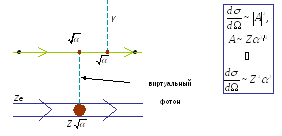
На рисунке красным кружком изображен не электрон, а любая заряженная частица с зарядом Ze.
В приближении малых углов рассеяния
(q << 1)
![]()
Электрическое поле частицы
![]()
![]() ,
,
![]() ,
,
![]() и
и
![]()
![]()
Интегрирование по
![]() от
0 до дает
от
0 до дает
![]()
Переданная энергия Т =
![]()
Или (если учесть, что тяжелая заряженная
частица пролетает мимо электрона среды
и заряд электрона Ze = e)
![]()
z (маленькое) – заряд пролетающей частицы в единицах заряда электрона