Файл: Лекция_1.doc

3. Среда наполнена атомами, атомные оболочки заполнены электронами (z – электронов на атом).

Плотность среды - ρ г/см³,

плотность атомов: nат= ρ·NА/A см^-3, где NА- число Авогадро,

плотность электронов: ne =Z·nат= Z/A ·ρ·NА см^-3 .

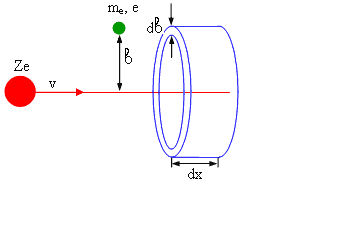
Если частица проходит в среде путь dx, то она взаимодействует почти одинаково со всеми электронами, которые располагаются на одном и том же расстоянии b от ее траектории, и каждому из них передает энергию Te. Количество таких электронов на пути dx будет определяться плотностью электронов и объемом кольцевого цилиндра длиной dx с внутренним радиусом b и внешним радиусом b+db . Объем этого цилиндра – 2πbdbdx. Электронов в нем будет:

ne=2bdbdxZ nат.

Каждому из этих электронов пролетающая частица передает энергию E, а всем электронам, находящимся на расстоянии b от нее в слое db на пути dx, частица передает энергию

* ne=2bdbdxZ nат

.

Энергия частицы при этом взаимодействии уменьшается, и поэтому производная dE(b)/ dx

отрицательна.

4. Чтобы найти ионизационные потери частицы на пути dx со всеми электронами среды, с которыми она взаимодействует с разными параметрами удара, надо проинтегрировать по всем возможным параметрам удара от bmin до bmax:

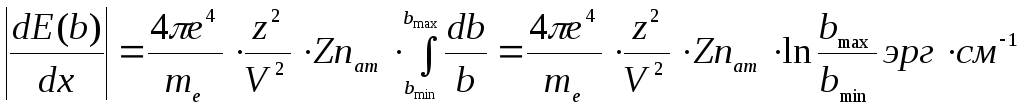
Пределы интегрирования должны быть конечны, так как из самых общих физических соображений удельные потери энергии (потери энергии на единицу длины пути) dE/dx должны иметь конечную величину - частица с конечной энергией не может потерять бесконечно большую энергию. Отсюда следует, что bmin≠0 и bmax≠ ∞. Рассмотрим, какими факторами

определяются величины предельных параметров удара bmin и bmax.

bmin

Минимальному значению параметра удара соответствует максимальная передаваемая энергия. Ранее был получено соотношение, связывающее передаваемую электрону

энергию с параметром удара b: Te = | E | = = .

---

Откуда имеем: b² = и, следовательно,

b²min = .

Если сталкиваются две частицы с массами М и me и M » me,

то максимальная передаваемая энергия будет:

.

Следовательно:

и .

В релятивистском случае в выражении для bmin появляется коэффициент , так как максимальная передаваемая энергия будет расти со скоростью частицы:

, а .

Итак, мы получили выражение для bmin с точки зрения классического подхода.

Можно найти минимальный параметр удара b′min с помощью квантово-механичеcкого

подхода, используя для этого соотношение неопределенностей .

Так как ,

то для b′min получаем:

в нерелятивистском случае

в релятивистском случае.

Обычно b′min > b min , поэтому используется классическое

выражение для bmin.

bmax

Чем больше параметр удара, тем меньше передаваемая электрону энергия Emin.

bmax соответствует случаю, когда передаваемая энергия близка к энергии связи этого электрона с ядром. Поскольку энергия связи разных электронов атома различна, то вводится обычно некоторая усредненная характеристика энергии связи электронов в атомах данного элемента (A,Z), называемая средним потенциалом ионизации I .

Для разных элементов I = I0·Z , где I0 слабо зависит от Z вещества.

В табл. приведены значения I0 для некоторых элементов.

вещество	Be	C	Воздух	Al	Cu	Pb
I0, эВ	16.0	13.0	12.8	12.8	11.1	10.0

---

Выбираем в качестве максимального прицельного параметра такой, при котором электрону передается энергия, равная среднему потенциалу ионизации: Emin = I. Так как

, то .

Теперь можно найти выражение для .

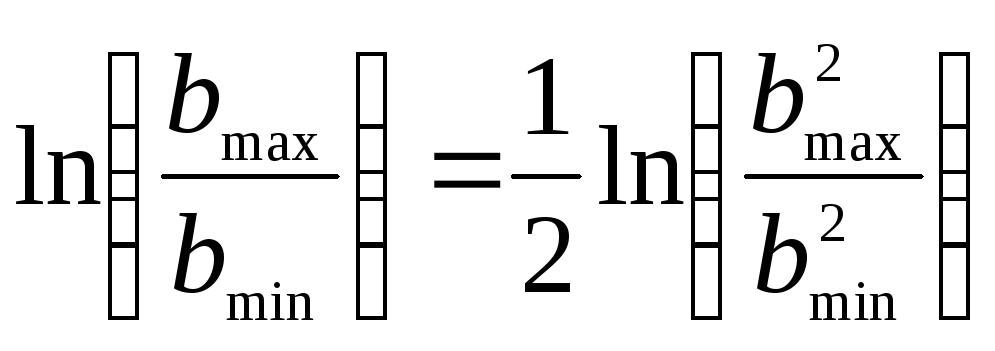Подставляя найденные нами значения bmax и bmin , получаем:

и

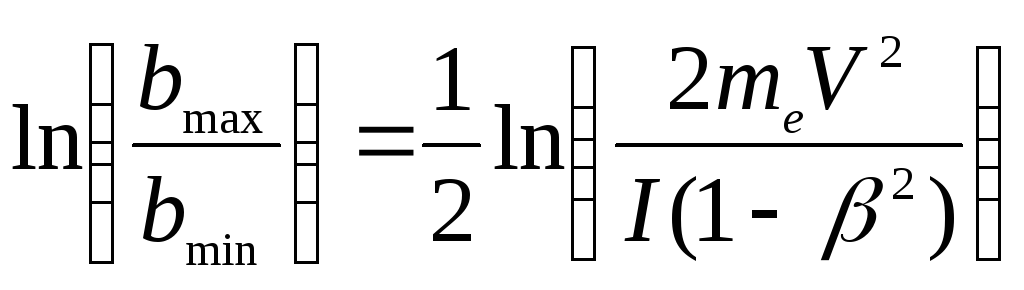
Выражение для удельных ионизационных потерь энергии частицы

(или линейная тормозная способность вещества):

приобретает вид:

- формула Бора

Нильс Бор

(1885 - 1962)

Вывод этой формулы на основе классических представлений первоначально был предложен Н.Бором в 1915 г., поэтому она и называется формулой Бора в этом виде или в уточненном варианте:

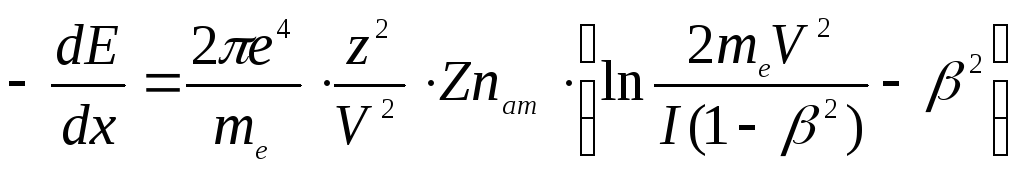- формула Бора в уточненом виде.

Ханс Бете Феликс Блох

(1906 - 2005) (1905 - 1983)

Позднее Г.А.Бете проделал аналогичные вычисления на основе квантовой механики.

В 1930-1933 гг. Г.А.Бете и Ф.Блохом были теоретически вычислены и получены из многочисленных экспериментальных данных величины bmin и bmax. Кроме того, в

1933 г. Ф.Блохом было предложено несколько иное выражение для среднего потенциала ионизации: I (Z) = Iн Z, где Iн = 13,5 эВ – энергия, соответствующая частоте Ридберга.

Формула для ионизационных потерь энергии, выведенная Бете и Блохом с учетом квантовых и релятивистских эффектов, называется их именем (формулой Бете-Блоха) и имеет вид:

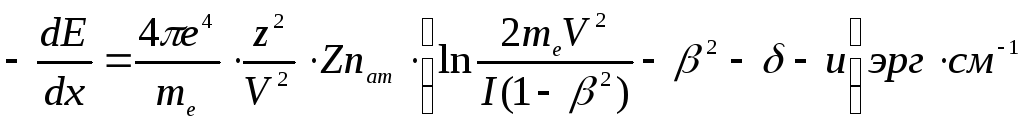- формула Бете-Блоха. (*)

"Bethe equation"

PDG http://pdg.lbl.gov/2013/reviews/rpp2013-rev-passage-particles-matter.pdf

---

(**)

= =

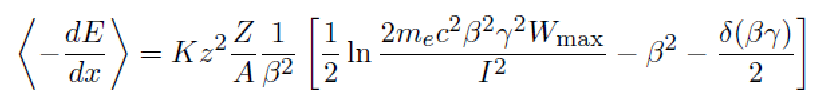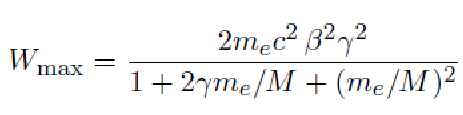
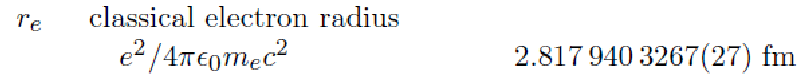
Варианты (*) и (**) можно совместить.

 

 

---

Почему релятивизм не проявился в коэффициенте перед логарифмом в формуле?

Причина в том, что этот коэффициент, как видно из вывода формулы, определяется величиной переданного импульса pe = F t. В случае релятивистских скоростей максимальное значение силы F, действующей со стороны частицы на электрон, увеличивается на множитель .

(Как указано в Теории поля, Ланд., Лифшиц закон Кулона пишется в особой системе координат, «сжатой» вдоль оси координат, вдоль которой движется частица )

С другой стороны время взаимодействия t уменьшается на множитель γ. Произведение их остается неизменным.

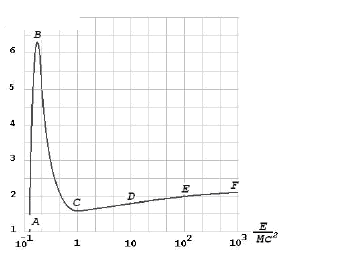
Рис. 3 Зависимость средних удельных ионизационных потерь энергии тяжелых частиц в свинце от энергии. Вся сложная кривая рисунка разделена буквами А, В, С, D, E, F

на отдельные участки с характерным для них поведением этой зависимости.

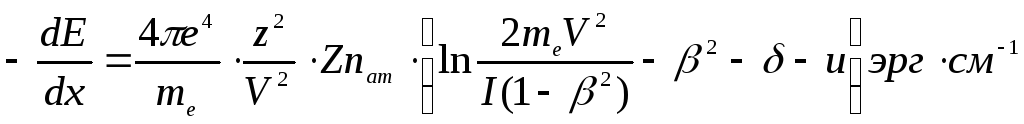
Зависимость ионизационных потерь от параметров частицы

(важное уточнение: до остановки частицы еще далеко)

1. Удельные ионизационные потери энергии (или линейная тормозная способность вещества):

пропорциональны квадрату заряда частицы: .

Это означает, что при одинаковой скорости ядро железа (z=26) теряет на ионизацию вещества в 676 раз больше энергии, чем протон.

2. Удельные потери не зависят от массы частицы М. Это получается из-за того,

что происходит взаимодействие электрических зарядов частиц, а не их масс. Однако, если сопоставлять потери на ионизацию различных частиц с одинаковой кинетической энергией, тогда в коэффициент перед логарифмическим членом неизбежно

войдет масса частицы, так как V²~ E/M. Поскольку в нерелятивистском случае ионизационные потери обратно пропорциональны квадрату скорости частицы:

---