ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.08.2024
Просмотров: 112
Скачиваний: 0
СОДЕРЖАНИЕ
Электромагнитные взаимодействия заряженных частиц
Способ классификации э/м взаимодействий
3. Среда наполнена атомами, атомные оболочки заполнены электронами (z – электронов на атом).
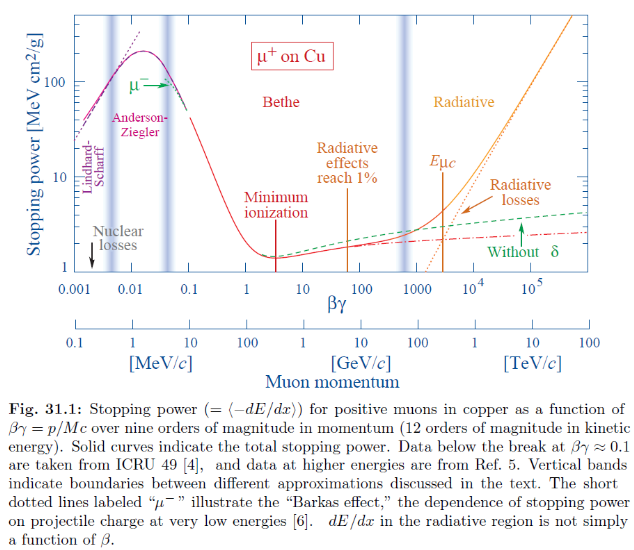
Почему релятивизм не проявился в коэффициенте перед логарифмом в формуле?
Домашнее задание.
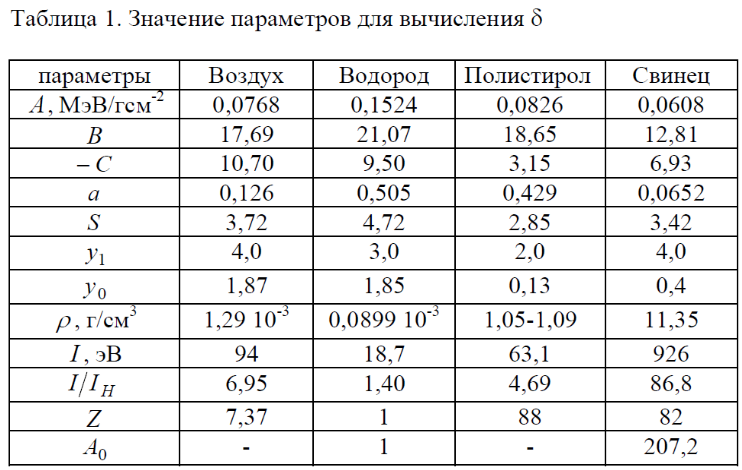
Исследовать формулу Бете-Блоха в "удобном " для расчета виде.
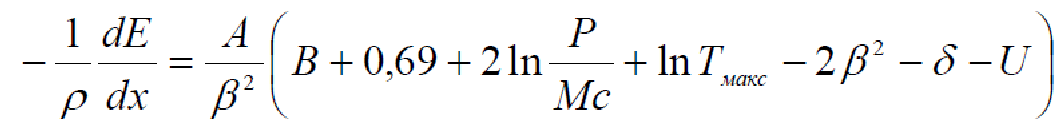
![]()
Принять U = 0.


ЯВЛЕНИЕ ПЕРЕЗАРЯДКИ
При рассмотрении ионизационного торможения тяжелых заряженных частиц (ионов атомов) нужно учитывать явление перезарядки, связанное с захватом частицей электронов вещества. Этот эффект становится существенным при скоростях частицы, сравнимых со скоростями орбитального движения электронов (АВ).
Эффективный заряд частицы уменьшается по мере снижения энергии. Для приближенных оценок можно воспользоваться следующим выражением для величины эффективного заряда частицы Ремизов В.С., Рогозкин Д.Б., Рязанов М.И. Флуктуации пробегов заряженных частиц. –
М.:Энергоатомиздат, 1988, с.240. ; Ковалев В.П.Эффективный заряд иона.- М.:Энергоатомиздат, 1991, с.168
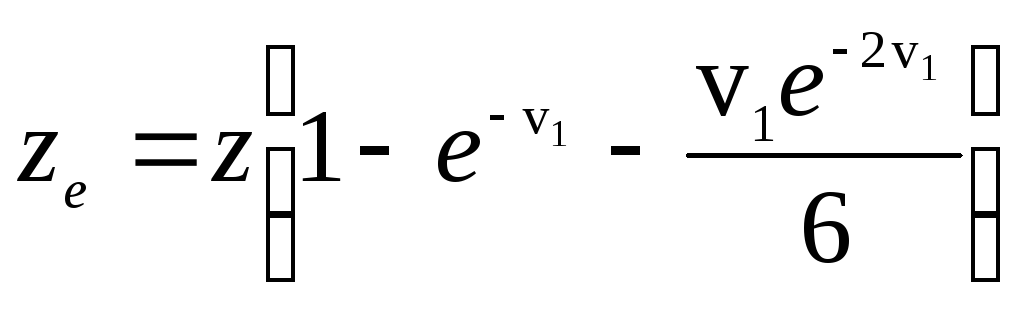 ,
где
,
где
![]() ;
;
![]() ;
z – заряд частицы.
;
z – заряд частицы.
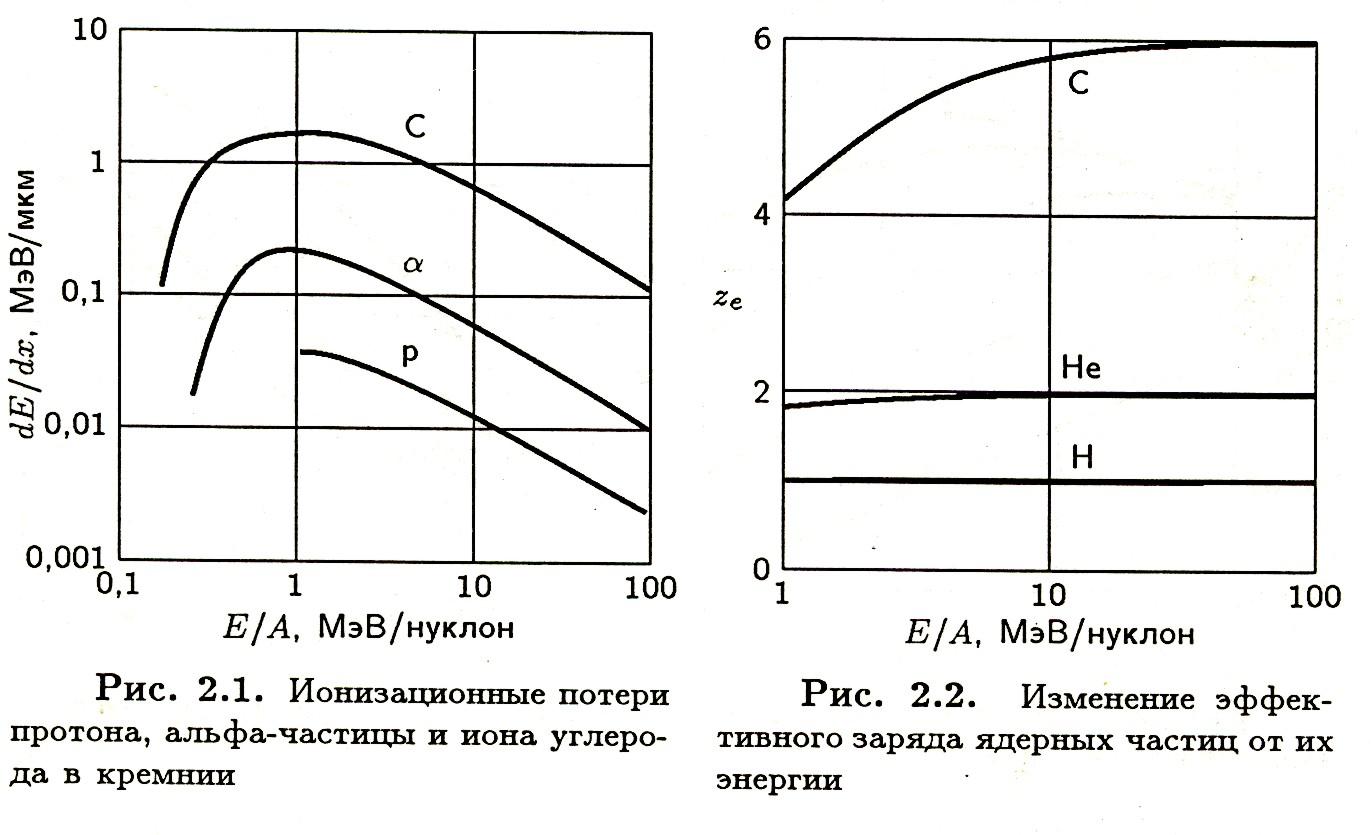
На Рис. представлен эффект изменения эффективного заряда протонов, -частиц и ионов углерода в кремнии в зависимости от энергии, нормированной на массу(атомный номер) частицы.
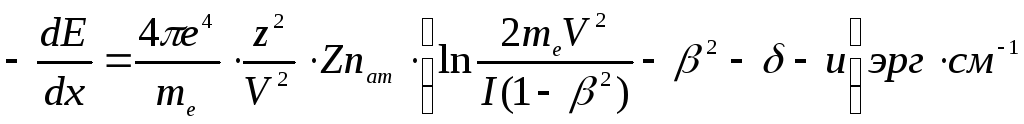
3ависимость ионизационных потерь от параметров среды
-
Положение максимума кривой (В) определяется Eгр для каждой среды, так как
![]() .
.
-
Удельные ионизационные потери энергии
(или линейные тормозные способности вещества):
Пропорциональны плотности электронов в среде:
![]()
В 1 см3 среды содержится электронов
![]()
где NA – число Авогадро, Z и A – заряд и атомный вес среды, а ρ – плотность среды.
Для легких веществ
![]() .
Следовательно, для этих сред
.
Следовательно, для этих сред
получается простая зависимость
![]() г/см3. Это обстоятельство
г/см3. Это обстоятельство
побудило ввести в обиход массовую единицу длины xρ, размерность которой [xρ] - г/см2. Смысл массовой единицы длины: это вес столбика вещества высотою x.
В массовых единицах формула Бете-Блоха принимает вид:
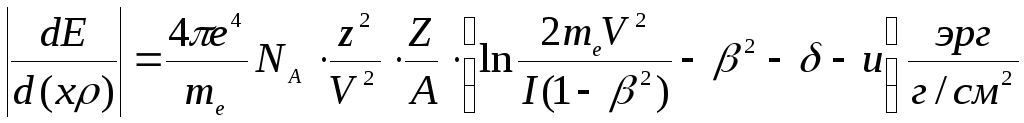
Поскольку Z/A~0.5, а I(A,Z) слабо влияет на величину потерь, так как входит под знаком логарифма, то оказывается, что при расчете на 1 г/см2 ионизационные потери во всех веществах
приблизительно одинаковы. Для иллюстрации сказанного в таблице 2.3 приведены ионизационные потери энергии однозарядных релятивистских частиц около минимума кривой, где E ≈(2-3) Mc2.
Таблица 2.3. Величина ионизационных потерь энергии в 1 г/см2
Вещества
-
Вещество
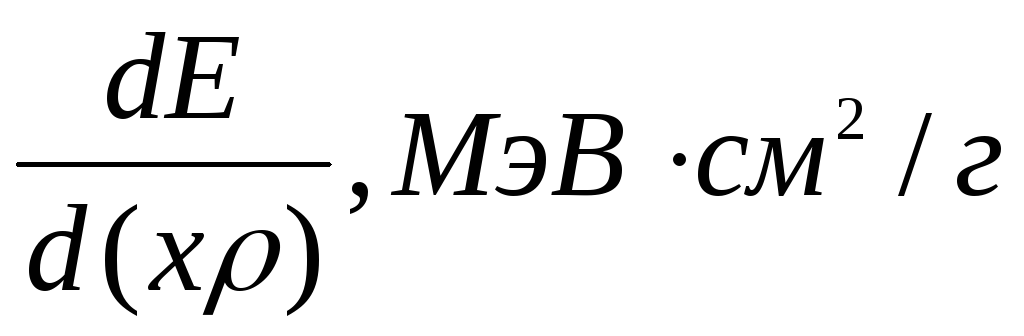
Воздух
1.8
Алюминий
1.65
Железо
1.5
Свинец
1.2
Как видно из табл.2.3, зависимость от A и Z слабая, но все же заметная
из-за того, что отношение Z/A уменьшается с ростом А.
3. Величина потенциала ионизации I(A,Z) уже обсуждалась ранее. И хотя потенциал ионизации входит под знаком логарифма и слабо сказывается на величине ионизационных потерь, тем не менее, для аккуратных вычислений его надо обязательно учитывать.
Правило Брэгга
S ir
William Henry Bragg
ir
William Henry Bragg
(1862 – 1942)
В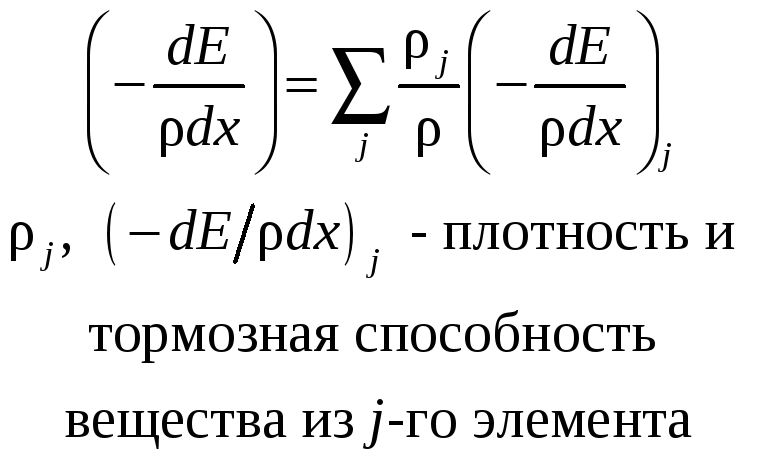 1905 г. австралийский физик Брэгг
сформулировал правило, согласно которому,
тормозная способность вещества, в чей
состав входят несколько химических
элементов, есть линейная комбинация
тормозных способностей этих элементов:
1905 г. австралийский физик Брэгг
сформулировал правило, согласно которому,
тормозная способность вещества, в чей
состав входят несколько химических
элементов, есть линейная комбинация
тормозных способностей этих элементов:
Если среда содержит атомы различных
элементов со своими характеристиками
Zi, Аi и ρi, , то плотность электронов в
среде будет зависеть от всех этих
величин, и можно считать с хорошей
степенью точности, что их тормозная
способность складывается (правило
Брэгга). В формуле Бете-Блоха для средних
ионизационных потерь в г/см2 вместо
Z/A и ln I появятся соответственно другие
величины:![]() и
и
![]()
![]() где
где
![]()
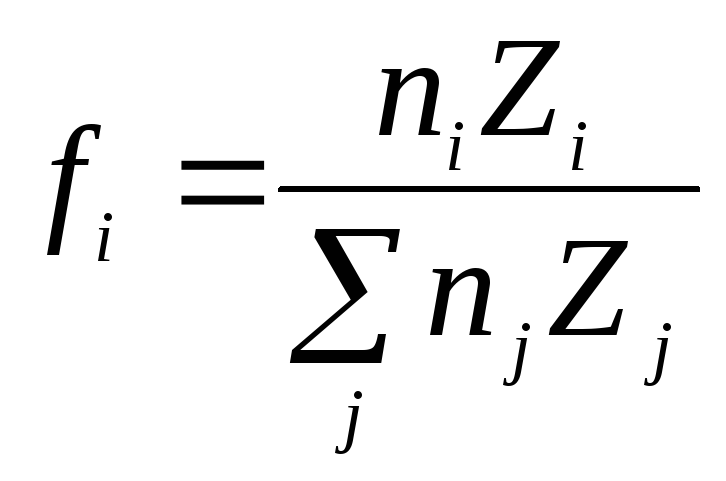 .
.
Здесь ni число атомов элемента с атомным номером Zi , Ii - средний потенциал ионизации атома с атомным номером Zi .
Пик Брэгга.
Кривой Брэгга называют график зависимости удельных ионизационных потерь от расстояния, пройденного заряженной частицей в веществе. В кривой Брэгга для тяжелых заряженных частиц наблюдается резко выраженный максимум в конце пробега, который носит название пика Брэгга.
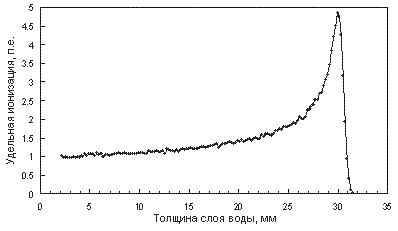
Рис. 2. Пик Брэгга при прохождении протонов с энергией 62 МэВ через воду
Радиационная медицина. Лечение опухолей потоками частиц.
При реальном лечении опухоль имеет не точечную структуру, а протяженную. Т.о. необходимо облучить протяженный участок, изменяя энергию мелким шагом (сдвигая пик кривой Брегга). График суммарной дозы, которую получат клетки при таком сканировании называется модифицированной кривой Брэгга (Spread Out Bragg Peak). На Рис. Представлены кривые Брэгга для протонов в диапазоне энергий от 100 до 110 МэВ, с шагом по энергии 1 МэВ, а также модифицированная кривая Брэгга.