Файл: Лекция_1.doc

, то .

С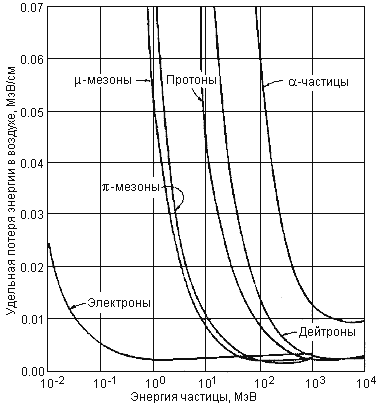ледовательно, частицы с одинаковой кинетической энергией теряют ее на ионизацию тем больше, чем больше их масса. Например, на единице своего пути дейтрон теряет на ионизацию энергию в 2 раза большую, чем протон с такой же кинетической энергией, а мюон в ~ 9 раз меньшую.

Рис. 1. Зависимость удельной потери энергии в воздухе от энергии частицы для нескольких типов частиц

Д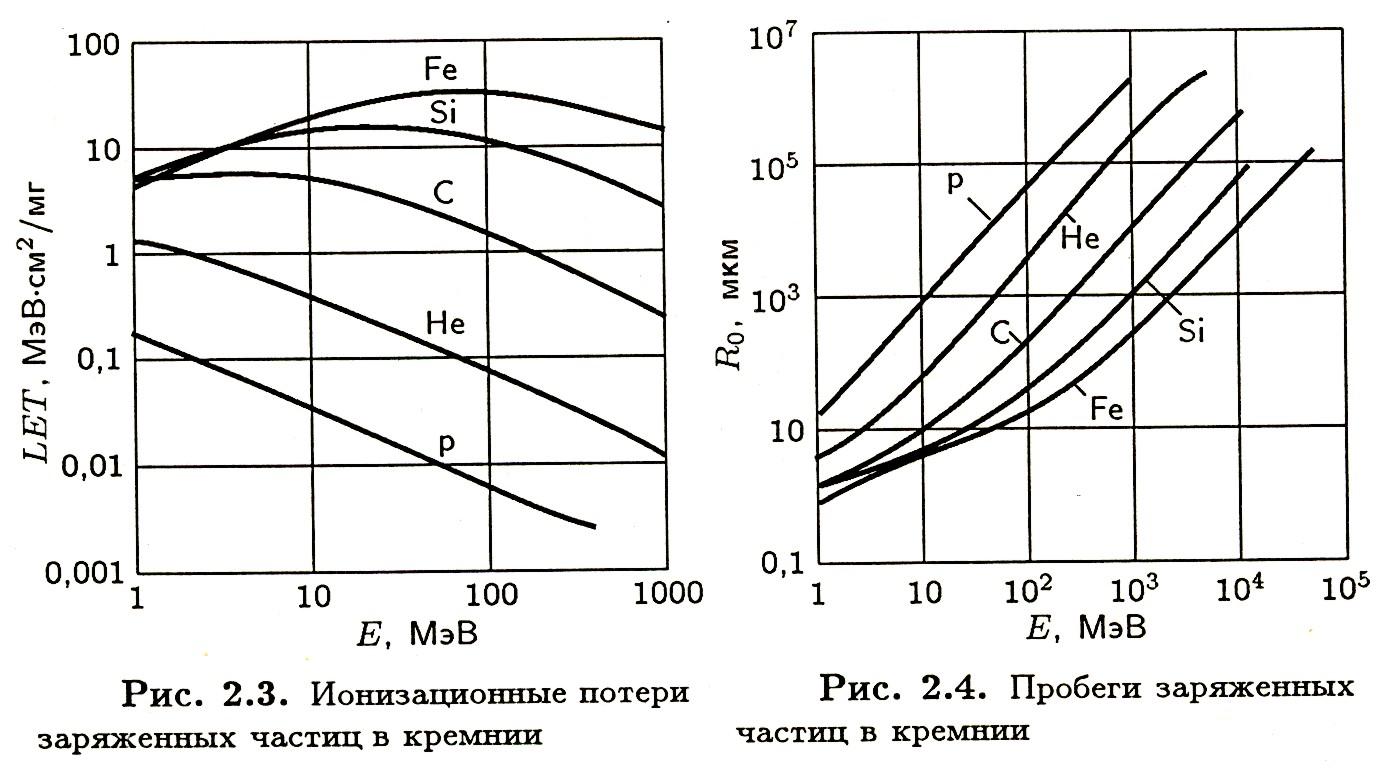ругой вариант иллюстрации ионизационных потерь энергии частицами с различными массами в кремнии представлен на рис. 2. (Почему в кремнии?)

Здесь потери энергии приведены не на единицу длины пути (в см), а на толщу вещества мг/см² – т.е. .

Массовая тормозная способность:

Рис.2. Ионизационные потери заряженных

частиц в кремнии .

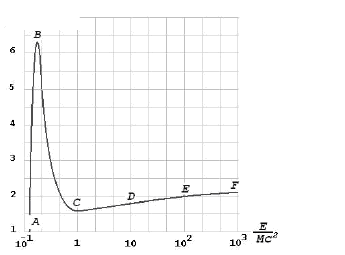
3. Удельные потери энергии на единице пути являются довольно сложной функцией скорости (и, следовательно, кинетической энергии) частицы. Эта зависимость схематически изображена на рис.3 , где по оси абсцисс отложена кинетическая энергия в единицах своей собственной энергии массы покоя Mc², а по оси ординат – средние удельные потери энергии этой частицей на ионизацию среды.

Рис. 3 Зависимость средних удельных ионизационных потерь энергии тяжелых частиц в свинце от энергии. Вся сложная кривая рисунка разделена буквами А, В, С, D, E, F

на отдельные участки с характерным для них поведением этой зависимости.

(BC). Участок (ВС) соответствует случаю, когда с, одной стороны, частица нерелятивистская, т.е. E < Mc² и  < 1, другой стороны, она настолько быстрая, что все электроны атомов могут считатьсясвободными. Поведение кривой в этой области (ВС) определяется коэффициентом перед квадратными скобками в формуле Бете-Блоха:

---

т.е. .

Такая зависимость в нерелятивистской области получилась из-за того, что переданный электрону импульс pe = F t, зависит от времени взаимодействия t, которое, в свою очередь, обратно пропорционально скорости частицы t ~ 1/ V. Переданная же

электрону энергия, потерянная частицей ~ 1/ V² , и , следовательно , ~ 1/E.

Зависимость имеет место вплоть до релятивистских скоростей. При V ≈ c коэффициент перед скобкой принимает минимальное значение.

(CD). На участке (СD) кривой (см. рис.4) удельные ионизационные потери начинают увеличиваться. Этот рост потерь обусловлен ростом величины логарифмического члена, так как при 1 .

Поскольку этот множитель стоит под знаком логарифма, то и рост потерь наблюдается медленный - "логарифмический". Логарифмическое возрастание с увеличением энергии обычно называют релятивистским подъемом ионизации. Он начинается после того, как достигнет минимальной величины при V  0.96с. Частично этот подъем

происходит за счет близких столкновений, так как увеличивается максимальная передаваемая энергия Emaх , а частично за счет далеких столкновений из-за релятивистского увеличения bmax. Рост потерь, обусловленный вторым фактором, происходит из-за релятивистского сжатия кулоновского поля частицы в продольном направлении (вдоль траектории частицы) и возрастания поля в поперечном направлении. Рис.5 иллюстрирует сказанное: для нерелятивистских частиц эквипотенциальная поверхность имеет сферически симметричную форму (а), а форма эквипотенциальной поверхности поля релятивистских частиц другая (б): расстояние в продольном направлении уменьшается в раз, а в поперечном - увеличивается в  раз, получается эллипсоид, "блин", который с увеличением скорости частицы все более сплющивается в продольном направлении и увеличивается в поперечном. Это означает, что все большее число электронов среды попадает в поле воздействия летящей частицы. Растет bmax и все большему числу электронов частица передает свою энергию. Следовательно, и потери энергии частицей на единице ее пути растут.

---

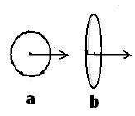
Рис. Форма эквипотенциальной поверхности кулоновского поля: (а) для нерелятивистской, (б) релятивисткой скорости частицы

---

Задача:

Вспомним как выглядит поле движущегося заряда.

Поля будем находить по обычным правилам, исходя из потенциалов A и  .

(DE). Казалось бы, эффект релятивистского сжатия поля должен был бы приводить к неограниченному увеличению потерь. Однако это не так. При дальнейшем увеличении энергии частицы bmax может стать больше расстояния между атомами среды. В этом случае возникает так называемый эффект плотности, который особенно существенен для плотных газов, жидкостей и, тем более, для твердых веществ. Эффект плотности связан с тем, что поле летящей частицы поляризует атомы среды. В результате поляризации многих атомов возникает поле диполей, направленное в сторону, противоположную полю летящей частицы. Оно ослабляет поле частицы и как бы экранирует от него далеко расположенные электроны. На некотором расстоянии от траектории частицы поле ее компенсируется полностью противоположным полем диполей.

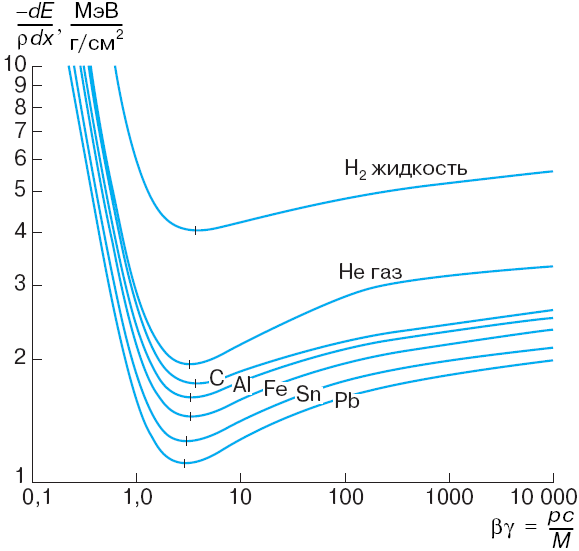
(EF). Область кривой (EF) и соответствует этому случаю: рост потерь энергии существенно замедляется из-за эффекта плотности. Остается только рост потерь за счет увеличения передаваемой энергии, которое обязанно росту Еmax. В формуле Бете-Блоха эффект плотности учитывается членом "δ". Поскольку эффект поляризации прямо пропорционален плотности электронов среды ne, то этот эффект в сильной степени зависит от плотности вещества, за что и получил свое название.

Энрико Ферми (1901 - 1954)

Поправка на эффект плотности в несколько упрощенном виде впервые была рассчитана Э.Ферми в 1939 г. и поэтому область (EF) часто называют "плато Ферми". В крайнем релятивистском случае поправка на эффект плотности дается выражением:

где , а 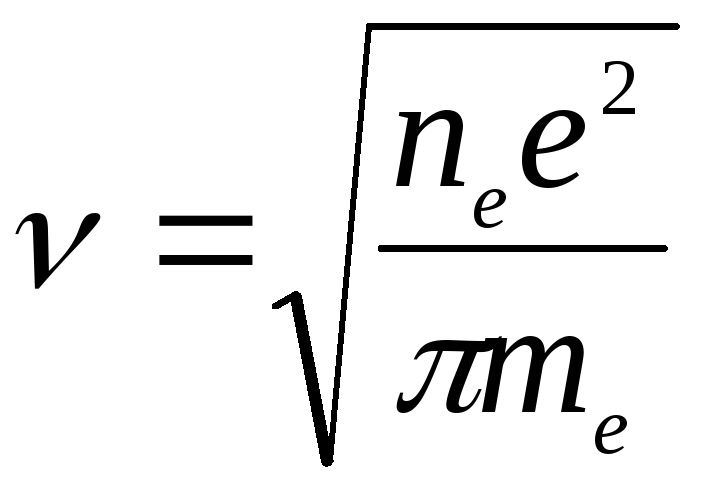- плазменная частота электронов.

В предельном случае очень больших энергий часть релятивистского возрастания потерь полностью компенсируется эффектом плотности. Оставшаяся часть связана с передачей энергии при близких столкновениях. В случае не очень больших энергий

максимальная передаваемая энергия Emax растет как . При очень высоких энергиях Emax возрастает приблизительно как , т.е. релятивистский подъем оказывается в три раза меньше того, который можно было ожидать без учета эффекта плотности.

---

Иногда употребляется понятие "ограниченные ионизационные потери" энергии, обычно связанное с условиями наблюдения, например, с ограничением пробега в трековом детекторе δ-электронов, получивших в результате ионизации максимальную энергию . Из-за этого регистрируется не максимальная передача энергии, а меньшая , т.к. она ограничена размерами детектора. В этом случае не будет наблюдаться рост ионизационных потерь в области (EF).

(АВ). Формула для ионизационных потерь была выведена в предположении, что все электроны атомов среды при взаимодействии с частицей могут считаться свободными, т.е. выполняется условие: , и .

По мере уменьшения энергии частицы это соотношение может оказаться нарушенным. В первую очередь это нарушение будет относиться к наиболее сильно связанным электронам в атомах: K- и L- электронам. Когда скорость частицы станет меньше скорости орбитального

движения K-электронов, ионизация их станет невозможной, и, следовательно, K-электроны должны быть выключены при вычислении плотности электронов в среде, т.е. число их как бы

уменьшится, и, соответственно, потери энергии также уменьшатся. При дальнейшем уменьшении скорости частицы то же самое следует отнести и к L-электроном, затем к М-электронам и т.д. Чем больше Z среды, тем больше εсв и тем выше граничная энергия частицы, при которой следует учитывать этот эффект. Поскольку , то граничная кинетическая энергия частицы будет

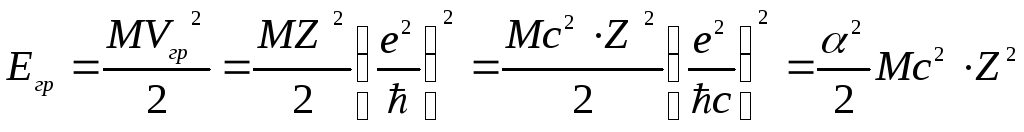
где α = 1/137 -постоянная тонкой структуры . В таблице 2.2 приведена граничная энергия для протонов и α-частиц в нескольких средах. Уменьшение потерь энергии при малых энергиях частицы соответствует левому "завалу" кривой ионизационных потерь (АВ), и в формуле Бете-Блоха учитывается последним членом u в квадратных скобках.

Таблица 2.2. Граничная энергия для протонов и α-частиц

Вещество	Егр для протонов, МэВ	Егр для α-частиц, МэВ
Углерод	0.9	3.6
Алюминий	4.2	16.9
Медь	21.0	84.4

---