ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.10.2024
Просмотров: 47
Скачиваний: 0
Таблица 4.2. Пример вероятностной оценки СВ
|
Номер интервала, j |
Интервал
|
Середина интервала xj, тыс.км |
Число отказов nj в интервале |
Частость (вероятность) ωi=рi |
Оценка накопленных вероятностей |
|
|
отказа F |
безотказности R |
|||||
|
1 |
6…8 |
7 |
60 |
0,06 |
0,06 |
0,94 |
|
2 |
8…10 |
9 |
120 |
0,12 |
0,18 |
0,82 |
|
3 |
10…12 |
11 |
190 |
0,19 |
0,37 |
0,63 |
|
4 |
12…14 |
13 |
250 |
0,25 |
0,62 |
0,38 |
|
5 |
14…16 |
15 |
200 |
0,20 |
0,82 |
0,18 |
|
6 |
16…18 |
17 |
130 |
0,13 |
0,95 |
0,05 |
|
7 |
18…20 |
19 |
50 |
0,05 |
1,00 |
0 |
|
Всего |
- |
- |
1000 |
1,00 |
- |
- |
Полученные при группировке СВ результаты сводятся в таблицу (табл. 4.1), данные которой имеют не только теоретическое, но и практическое значение. Например, по результатам наблюдений можно предположить, что у аналогичных изделий в тех же условиях эксплуатации и в интервале наработки 6…8 тыс. км может отказать около 6 % изделий (ωi=pi= 0,06), в интервале 8…10 тыс. км – 12 %, интервале 10…12 тыс. км – 19 % и т.д.
Следовательно, имея систематизированные данные по отказам, можно прогнозировать и планировать число воздействий (программу работ), потребности в рабочей силе, площадях, материалах и запасных частях.
4.4.3.1 Вероятность случайного события. В общем виде это отношение числа случаев, благоприятствующих данному событию, к общему числу случаев.
Вероятность отказа рассматривается не вообще, а за определенную наработку X:
![]() ,
(4.9)
,
(4.9)
где т(х) – число отказов за X, п – число наблюдений (изделий), или вероятность отказа изделия при наработке Х равна вероятности событий, при которых наработка до отказа конкретных изделий хi окажется менее X. В примере (табл. 4.1) при Х = 10 тыс. км имеем
![]() .
.
Отказ и безотказность являются противоположными событиями, поэтому
![]() ,
(4.10)
,
(4.10)
где п - т(х) – число изделий, не отказавших за X.
В примере для Х = 10 тыс. км имеем
![]() .
.
Обычно применяется следующая буквенная индексация рассмотренных событий и понятий:
F (failure) – отказ, авария, повреждение, вероятность этих событий;
R (reliability) – безотказность, надежность, прочность, вероятность этих событий;
Р (probability) – вероятность.
Вероятность отказа может быть получена также последовательным суммированием интервальных вероятностей за наработку X, т.е.
F(x)=p1+p2+…pj , (4.11)
где j - номер интервала, соответствующий наработке X.
4.4.3.2. Следующей характеристикой случайной величины является плотность вероятности (например, вероятности отказа) f(х) - функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку F(х) = т(х)/п, то, дифференцируя ее при п=const, получим плотность вероятности отказа
![]() ,
(4.12)
,
(4.12)
где dm/dx – элементарная "скорость", с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.
Так как f(х) = F'(х), то
![]() .
(4.13)
.
(4.13)
Поэтому F(х) называют интегральной функцией распределения, а f(х) – дифференциальной функцией распределения.
Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
(4.14)
.
(4.14)
Имея значения F(х) или f(х), можно произвести оценку надежности и определить среднюю наработку до отказа
![]() .
(4.15)
.
(4.15)
4.4.3.3. При оценке качества изделий, нормировании ресурсов, в системе гарантийного обслуживания применяют гамма-процентный ресурс хγ. Это интегральное значение ресурса Хγ, которое вырабатывает без отказа не менее γ процентов всех оцениваемых изделий, т.е.
![]() .
(4.16)
.
(4.16)
В ТЭА обычно принимаются γ = 80, 85, 90 и 95 %. Для тракторов и автомобилей нормативное значение γ = 80 %.
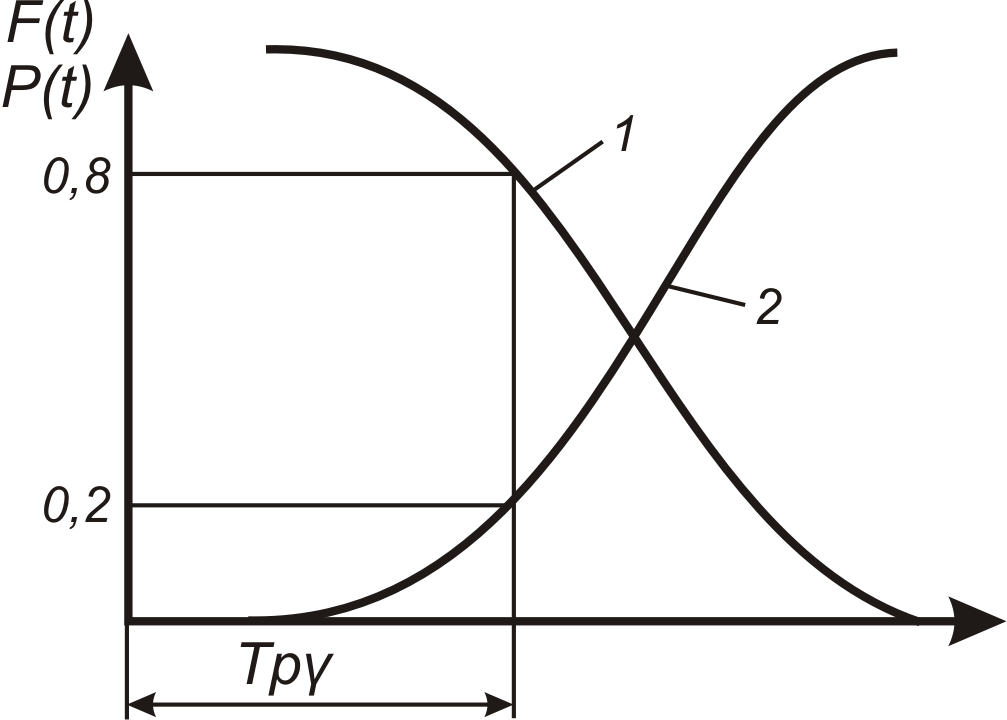
Рис. 4.4. – Определение 80%-го гамма-ресурса графическим методом по кривым интегральной функции вероятности безотказной работы (1), отказа (2)
В рассматриваемом примере при γ = 95 % хγ = 7 тыс. км (табл. 4.1). Риск отказа изделия F в данной ситуации, т.е. более раннее достижение изделиями гамма-процентного ресурса, составляет около 5 %.
Гамма-процентный ресурс, используется при определении периодичности ТО по заданному уровню безотказности γ. Выражение lТО = Хγ означает, что обслуживание с периодичностью lТО гарантирует вероятность безотказной работы R≥γ и отказа F≤(1-γ).
4.4.3.4. Важным показателем надежности является интенсивность отказов λ(х) – условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Аналитически для получения λ(х) необходимо элементарную вероятность dm/dx отнести к числу элементов, не отказавших к моменту х, т.е.
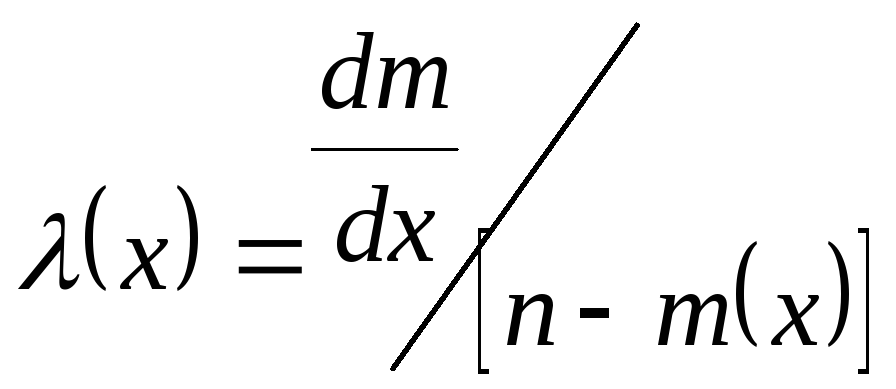 .
(4.17)
.
(4.17)
Так как вероятность безотказной работы R(х) = [п - т(х)]/ п, то λ(х)= dm/dx*1/nR(x). Учитывая, что f(х)=1/ndm/dx получаем
![]() .
(4.18)
.
(4.18)
Таким образом, интенсивность отказов равна плотности вероятности отказа, деленной на вероятность безотказной работы для данного момента времени или пробега
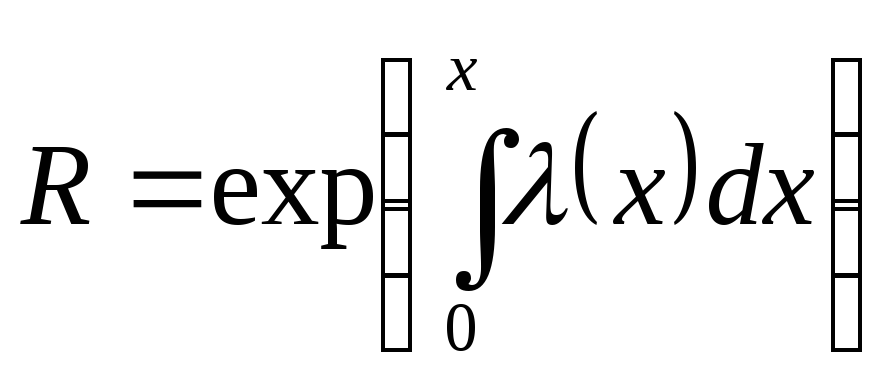 .
(4.19)
.
(4.19)
Это универсальная формула определения вероятности безотказной работы невосстанавливаемого элемента для любого закона распределения. Зная интенсивность отказов, можно для любого момента времени или пробега определить вероятность безотказной работы. Существуют внезапные и постепенные отказы. Постепенные отказы описывают работу так называемых стареющих элементов.
4.4.3.5. Наглядное представление о величине и вариации случайных величин дает их графическое изображение: гистограммы (1, рис. 4.5) и полигоны (2, рис. 4.5) распределения, а также интегральные функции распределения вероятностей отказа (3, рис. 4.5) и безотказной работы (4, рис. 4.5) и дифференциальные функции или законы распределения случайной величины (рис. 4.6, 4.7, 4.8).
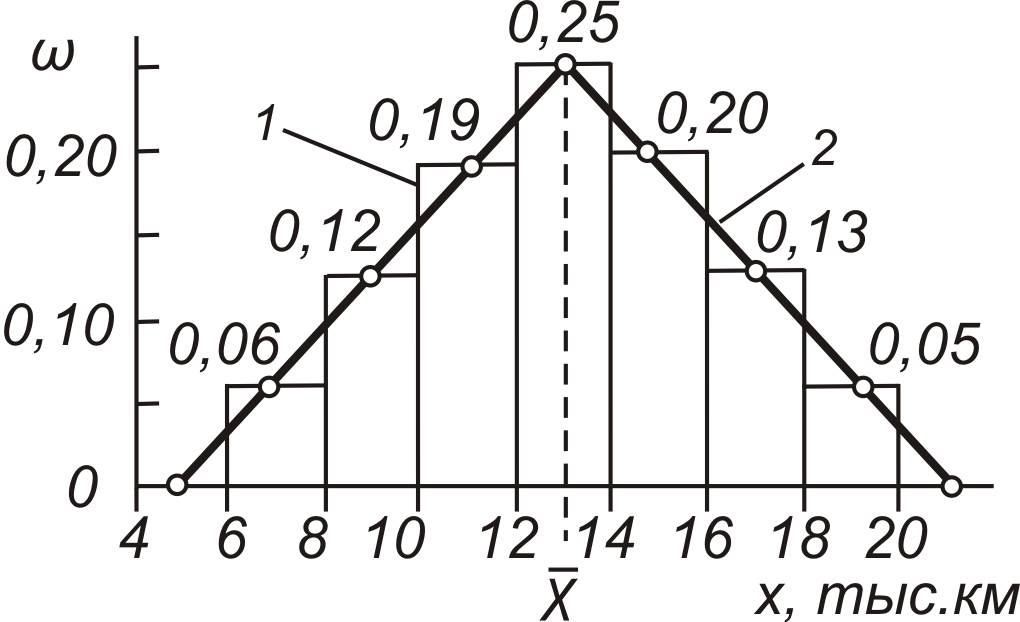
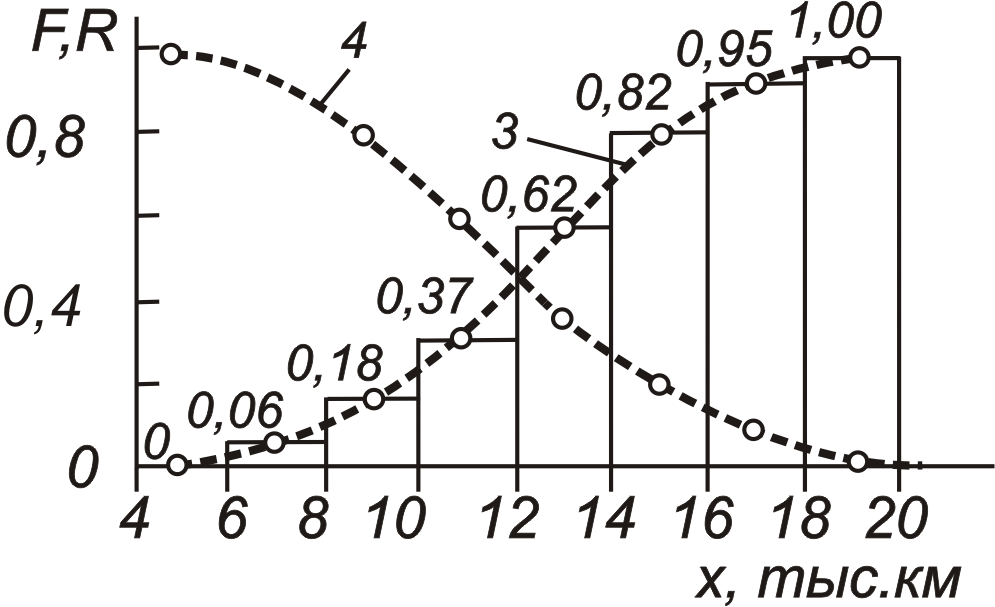
Рис. 4.5. Графическое изображение случайной величины: 1 – гистограмма, 2 – полигон распределения, 3 – интегральная функция вероятности отказов и 4 – безотказной работы